POJ3083 Children of the Candy Corn BFS+DFS

题目大意：给出一个n*m的迷宫和起点S以及终点E，让你找出一下三种迷宫求解结果：（1）左转优先搜索；（2）右转优先搜索；（3）迷宫最短路线；

分析：前两者可以借助DFS来完成，对于最短路线，就只能用BFS了。

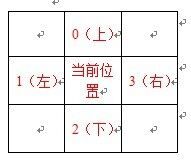
我们首先来考虑一下怎么实现左转优先，对于下图来说，最初的方向由起点S确定，而下一步的方向则由前一步的

方向决定。

例如 左边优先搜索：

当前位置的方向指向 1（向左），(这同时说明前一步是在第“3”的位置走过来的)

那么走下一步时，就要根据2103的顺序，先逐格确定当前位置周边的四格是否可行

若第一次确认2可行，就走到2，在位置2时的方向为2（向下）

若2不可行，则再确定1，若1可行，就走到1，在位置1时的方向为1（向左）

若1也不可行，则再确定0，若0可行，就走到0，在位置0时的方向为0（向上）

若0也不可行，说明进入了迷宫的死胡同，要从原路返回，走回3
 
右边优先搜索也同理。
 
如果我们设当前位置为d，那么

左转时用数学式子表达就是  d=(d+1)%4

右转时用数学式子表达就是  d=(d+3)%4

参考别人的代码才过的=_=！

实现代码如下；

#include<cstdio>
#include<cstring>
using namespace std;
int n,m;
int r[4][2]= {{0,-1},{1,0},{0,1},{-1,0}};
int l[4][2]= {{0,1},{1,0},{0,-1},{-1,0}};
bool s[50][50];
char map[50][50];
int sx,sy,ex,ey,ans;
int que[2500][2];
int dfs1(int x,int y,int step)
{
    if(x==ex&&y==ey)
        return step+1;
    if(x<0||x>=n||y<0||y>=m||map[x][y]=='#')
        return 0;
    ans=(ans+3)%4;
    int temp=0;
    while(1)
    {
        temp=dfs1(x+l[ans][0],y+l[ans][1],step+1);
        if(temp>0) break;
        ans=(ans+1)%4;
    }
    return temp;
}
int dfs2(int x,int y,int step)
{
    if(x==ex&&y==ey)
        return step+1;
    if(x<0||x>=n||y<0||y>=m||map[x][y]=='#')
        return 0;
    ans=(ans+3)%4;
    int temp=0;
    while(1)
    {
        temp=dfs2(x+r[ans][0],y+r[ans][1],step+1);
        if(temp>0) break;
        ans=(ans+1)%4;
    }
    return temp;
}
int bfs()
{
    int fir=0,sec=0;
    que[sec][0]=sx;
    que[sec++][1]=sy;
    s[sx][sy]=1;
    int step=1;
    while(fir<sec&&!s[ex][ey])
    {
        int tmp=sec;
        step++;
        while(fir<tmp&&!s[ex][ey])
        {
            int x=que[fir][0];
            int y=que[fir++][1];
            for(int i=0; i<4; i++)
            {
                int x1=x+r[i][0];
                int y1=y+r[i][1];
                if(x1>=0&&x1<n&&y1>=0&&y1<m&&!s[x1][y1]&&map[x1][y1]!='#')
                {
                    que[sec][0]=x1;
                    que[sec++][1]=y1;
                    s[x1][y1]=1;
                }
            }
        }
    }
    return step;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d",&m,&n);
        memset(que,0,sizeof(que));
        memset(s,0,sizeof(s));
        for(int i=0; i<n; i++)
        {
            scanf("%s",map[i]);
            for(int j=0; j<m; j++)
            {
                if(map[i][j]=='S')
                {
                    sx=i;
                    sy=j;
                }
                if(map[i][j]=='E')
                {
                    ex=i;
                    ey=j;
                }
            }
        }
        ans=0;
        printf("%d",dfs1(sx,sy,0));
        ans=0;
        printf(" %d",dfs2(sx,sy,0));
        printf(" %d\n",bfs());
    }
    return 0;
}