PKU1737 解题报告 Connected Graph __高精度加法,乘法,减法,组合数
Connected Graph
链接地址
http://acm.pku.edu.cn/JudgeOnline/problem?id=1737
时空限制
Time limit:1 Seconds Memory limit:30000K
题目内容
Description
An undirected graph is a set V of vertices and a set of E∈{V*V} edges.An undirected graph is connected if and only if for every pair (u,v) of vertices,u is reachable from v.
You are to write a program that tries to calculate the number of different connected undirected graph with n vertices.
For example,there are 4 different connected undirected graphs with 3 vertices.
Input
The input contains several test cases. Each test case contains an integer n, denoting the number of vertices. You may assume that 1<=n<=50. The last test case is followed by one zero.
Output
For each test case output the answer on a single line.
Sample Input
1
2
3
4
0
Sample Output
1
1
4
38
Source
LouTiancheng@POJ
解题思路(算法)
题目大致意思是给定n个点,求这n个点的连通图的个数。
用g(n)表示n个点总共可以表示成几个图,因为总共有n*(n-1)/2条边,而这n*(n-1)/2中每条边连或不连有两种可能,所以g(n)=2^(n*(n-1)/2)
所以连通图的个数=总的图的个数-不是连通图的个数;
那令f(n)表示n个点的连通图的个数;
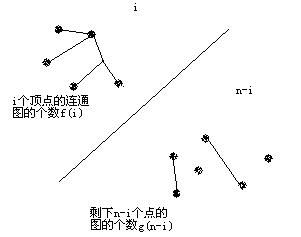
而不连通的图的个数是顶点数小于n的连通图的个数乘以剩下的顶点总共的图的个数,即
;如图 :
但是…
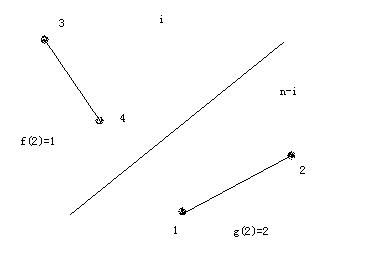
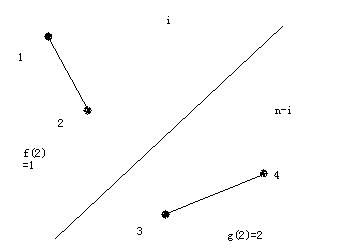
真的是Cin吗,看一个例子
1)和2)其实是同一种状态,但是按 算选出(1,2)是一种,选出(3,4)是一种,所以产生了重复。
那么该怎么修改呢,其实只要固定一个点,假设是1,再从n-1个点中选出i-1个点去跟1构成连通图即Ci-1n-1,那样就可以避免重复了;
因为n=11时数据就已经达到
35677592006776576了;
N=12的话就超过__int64的范围了。
所以此题必然要用到高精度了。
在计算f,Cin的时候把f,Cin算出来后保存下来,避免重复计算,否则有可能超时。
还有个要注意的就是:计算Cin时可以用公式Cin= Ci-1n+Ci-1n-1,这样就可以用高精度加法递推出来了。
程序代码
#include<stdio.h>
#include<memory.h>
int CC[60][60][400];
int FF[60][1000];
int GG[60][1000];
int gjd_add(int *a,int *b,int *c)
{
int i;
for(i=*a+1;i<=*a+*b+5;i++) a[i]=0;
for(i=*b+1;i<=*a+*b+5;i++) b[i]=0;
for(i=1;i<=(*a+*b+5);i++) c[i]=a[i]+b[i];
for(i=1;i<=*a+*b+3;i++)
{
c[i+1]=c[i+1]+c[i]/10;
c[i]=c[i]%10;
}
for(i=*a+*b+4;i>=1;i--)
if (c[i]) break;
c[0]=i;
return i;
}
int gjd_min(int *a,int *b)
{
int i;
for(i=1;i<=*b;i++)
a[i]=a[i]-b[i];
for(i=1;i<=*a;i++)
if (a[i]<0)
{
a[i+1]--;
a[i]+=10;
}
for(i=*a;i>=1;i--)
if (a[i]) break;
a[0]=i;
return i;
}
int gjd_mul(int *a,int *b,int *c)
{
int i,j;
for(i=*a+1;i<=*a+*b+5;i++) a[i]=0;
for(i=*b+1;i<=*a+*b+5;i++) b[i]=0;
for(i=0;i<=*a+*b+5;i++) c[i]=0;
for(i=1;i<=*a;i++)
for(j=1;j<=*b;j++)
c[i+j-1]+=a[i]*b[j];
for(i=1;i<=*a+*b+5;i++)
{
c[i+1]=c[i+1]+c[i]/10;
c[i]=c[i]%10;
}
for(i=*a+*b+5;i>=1;i--)
if (c[i]) break;
c[0]=i;
return i;
}
int g(int n)
{
int i,j;
int temp1[1000],temp2[1000];
if (GG[n][0]) return GG[n][0];
if (n==1) {
GG[1][0]=1;
GG[1][1]=1;
return 1;
}
memset(temp1,0,sizeof(temp1));
memset(temp2,0,sizeof(temp2));
temp2[0]=1;temp2[1]=2;
temp1[0]=1;temp1[1]=1;
for(i=1;i<=(n-1)*n/2;i++)
{
gjd_mul(temp1,temp2,GG[n]);
for(j=0;j<=GG[n][0];j++) temp1[j]=GG[n][j];
}
return j;
}
int C(int x,int y)
{
int i,j;
if (CC[x][y][0]) return CC[x][y][0];
if ((x==y)||(x==0))
{
CC[x][y][0]=1;
CC[x][y][1]=1;
return CC[x][y][0];
}
C(x,y-1);C(x-1,y-1);
gjd_add(CC[x][y-1],CC[x-1][y-1],CC[x][y]);
return CC[x][y][0];
}
int f(int n)
{
int i,j,k,t,ans,temp[1000],temp1[1000];
if (FF[n][0]) return FF[n][0];
memset(temp,0,sizeof(temp));
g(n);
gjd_add(temp,GG[n],FF[n]);
for(i=1;i<=n-1;i++)
{
C(i-1,n-1);f(i);gjd_mul(GG[n-i],FF[i],temp1);
gjd_mul(temp1,CC[i-1][n-1],temp);
gjd_min(FF[n],temp);
}
}
int main()
{
int n,i,j,k;
memset(FF,0,sizeof(FF));
memset(GG,0,sizeof(GG));
memset(CC,0,sizeof(CC));
while((scanf("%d",&n),n)!=0)
{
f(n);
for(i=FF[n][0];i>=1;i--)
printf("%d",FF[n][i]);
printf("/n");
}
return 0;
}
汉语翻译
1.题目
一个无向图就是有v个顶点和e条边(E∈{V*V})构成的一个集合。如果一个无向图对于每个点对(u,v)都可以从u通过边到底v,那么这个图就是连通的,你的任务就是写一个程序来计算总共有多少个不同的包含n个顶点的连通的无向图;
像下面这个例子,总共有4个不同呢的包含3个顶点的连通的无向图:
2.输入描述
输入包括多组数据,每个数据包含一个整数n,表示顶点数(1=<n<=50)。
输入以0为结束标志。
3.输出描述
对于每个测试点用一行输出结果。