STL源码剖析之红黑树【2013.12.05】
STL源码剖析之红黑树【2013.12.05】
欢迎加入我们的QQ群,无论你是否工作,学生,只要有c / vc / c++ 编程经验,就来吧!158427611
【红黑树】
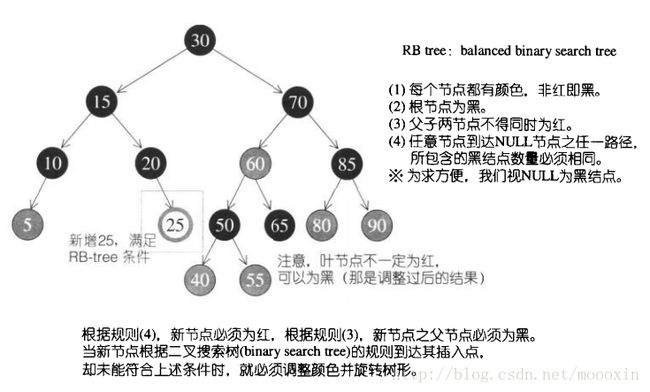
红黑树是一种受限制的搜索树,其限制如下:

【红黑树的节点插入】
为了方便解说,闲定义几个数值:
【X】插入节点,插入点必为红色,保持约束4
【P】X的父节点
【G】P的父节点
【GG】G的父节点
【S】P的兄弟节点
根据红黑树节点的插入,可以分为几种情况:
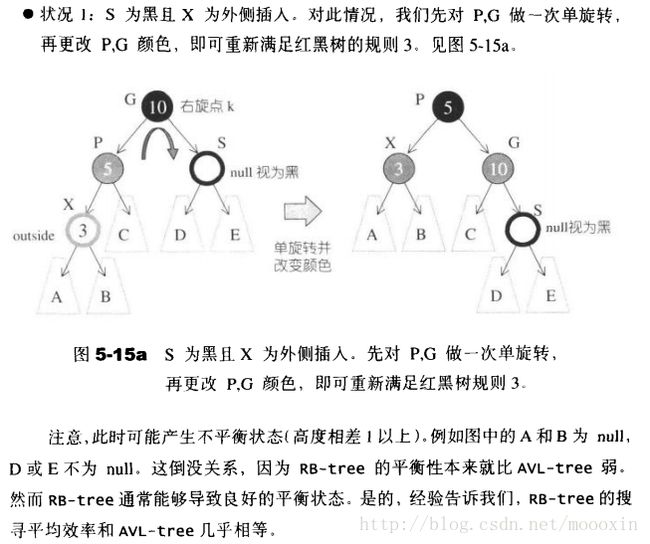
【一】
此情况:
只需要进行一次旋转就可以保持红黑树特性;
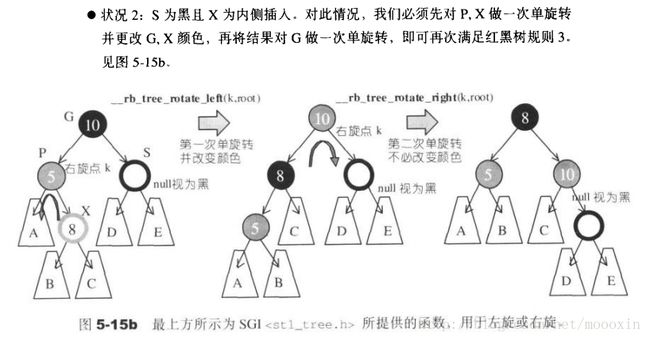
【二】
此情况,需要两次旋转才能保持红黑树的特性
【三】
此情况,也只需要一次旋转就可以完成
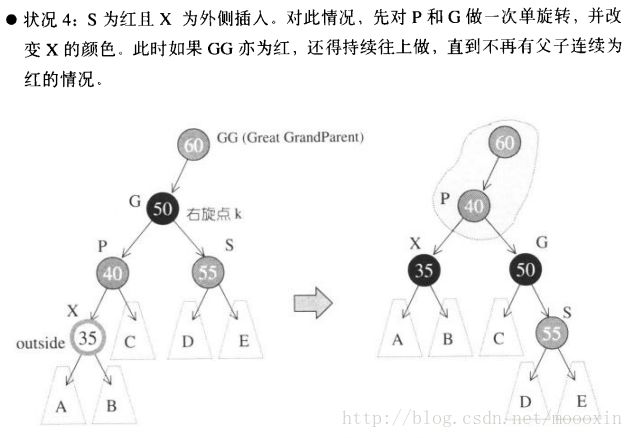
【四】
此情况也只需要一次旋转就能完成。
这种情况,需要向上递归寻找父节点,判断父节点的红黑情况,在树比较小的时候虽然可以接受,但是当树比较大的时候就是一种比较大的效率开销了。
怎么办呢?
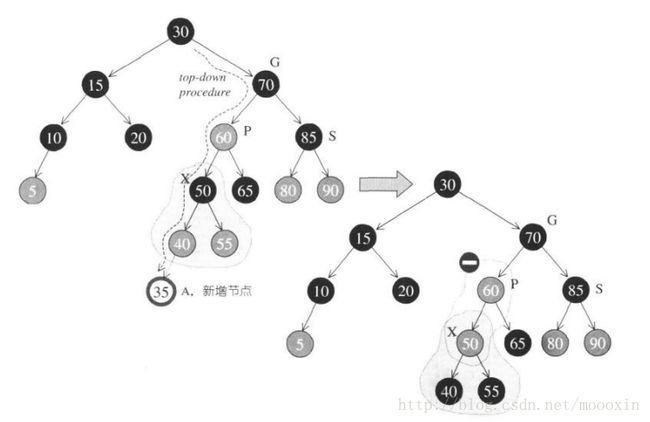
办法当然被牛人们想到啦,对红黑树做一个自顶向下的遍历。当然是沿着插入点路径了。
当遇到路径上某个节点【M】的两个子节点都为红色的时候:将【M】点变成红色,两个子节点变成黑色。(参考约束4),如图所示:
另外要注意的一点,虽然红黑树是一种搜索树,是平衡二叉树
但是其实红黑树对平衡的要求不是那么严谨的,有时候可能不会做到平衡,但是仍保持搜索树的其他特性。
STL中,红黑树的节点代码设计比较特别的一点是:
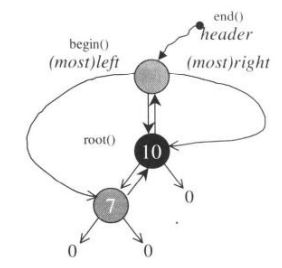
ROOT根节点之上 还有个 Header节点。
他们不但互相为父子节点,而且Header节点的Left指向红黑树中最小节点,Right指向最大节点。
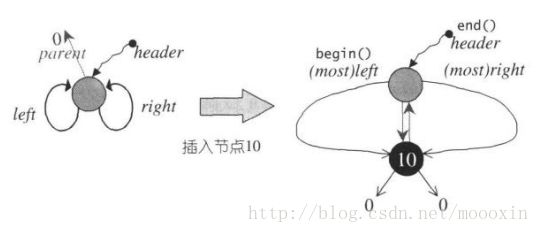
当然初始状态的时候,只有Header点,这时候,left和right都是指向自己,parent则是指向0(NULL)
当插入第一个节点的时候,即为根节点的时候,就看作最大最小值都是ROOT节点,Header和ROOT的关系就不但互相指向父子节点,而且left和right都指向Root。如图所示:
为什么这样做呢?
【原因1】:这样可以快速找到红黑树的最小最大值。
【原因2】:STL中红黑树是有++ 和 -- 两种操作符的,说明红黑树是可以递增递减遍历的,这样的设计就可以让迭代器快速找到begin和end啦。对效率来说是一种很巧妙的设计!
【注意】
红黑树的构造,主要功效就是做搜索,这也是红黑树的最大生命意义了,呵呵!
至于STL中红黑树的搜索,就不多说了。
比较节点,节点值比搜索值大的往左走,小的往右走。
欢迎加入我们的QQ群,无论你是否工作,学生,只要有c / vc / c++ 编程经验,就来吧!158427611