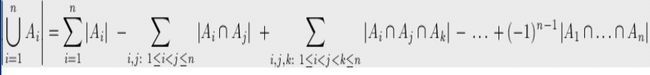相同数不能相邻的排列问题 组合数学-容斥原理

题目：1、2、3、4、5各有两个，组成一个十位数，要求相同的数不能相邻，有多少种排法?

思路：

两组数，每组5个各不相同的数，一共是5对儿，进行排列：

0、如果没有要求相同数不相邻，则有10!/(2^5)种排列，记作C。

1、如果要求有一对相邻的，那么把这一对儿数看成一个数，则有C(5, 1)*9!/(2^4)种排列，记作C1。

2、如果要求有两对相邻的，那么把这两对儿数看成两个数，则有C(5, 2)*8!/(2^3)种排列，记作C2。

3、如果要求有三对相邻的，那么把这三对儿数看成三个数，则有C(5, 3)*7!/(2^2)种排列，记作C3。

4、如果要求有四对相邻的，那么把这四对儿数看成四个数，则有C(5, 4)*6!/(2^1)种排列，记作C4。

5、如果要求这五对儿数都相邻，那么就是五个数全排列，C(5, 5)*5!/(2^0) = 5!，记作C5。

目标问题：要求五对数全都不相邻的排列。那么就是，没有要求的排列计数 - 有相邻的排列计数。

根据容斥原理的概念，把相邻事件的发生看做是一种集合，则有5个集合，集合1是数字1相邻的集合，集合2是数字2相邻的集合，集合3是数字3相邻的集合，集合4是数字4相邻的集合，那么问题变为求这5个集合的并集的card。显然，C1是所有单个集合的card之和，C2是所有两个集合相交的card之和，C3是所有三个集合相交的card之和，C4是所有四个集合相交的card之和，C5是所有五个集合（即所有集合）相交的card之和。

由此，可以使用容斥定理的公式，得到有相邻事件的排列计数，为C1-C2+C3-C4+C5。那么，没有要求的排列计数 - 有相邻的排列计数=C-(C1-C2+C3-C4+C5)。

所以这道题的结果为10!/(2^5)-9!*C(5,1)/(2^4)+8!*C(5,2)/(2^3)-7!*C(5,3)/(2^2)+6!*C(5,4)/(2^1)-5! = 39480

容斥原理：

容斥原理是组合数学中的重要概念和定理。在计数时，必须无一重复，且无一遗漏。

其基本思想是，先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复。

其基本过程是，要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

其一般公式如下所示：

|S1 ∪ S2 ∪ ... Sn| =(|S1| + |S2| + ... |Sn|)
  − (|S1 ∩ S2| + |S1 ∩ S3| + ... |Sn − 1 ∩ Sn|)
  + (|S1 ∩ S2 ∩ S3| + |S1 ∩ S2 ∩ S4| + ... |Sn − 2 ∩ Sn − 1 ∩ Sn|)
  − (|S1 ∩ S2 ∩ S3 ∩ S4| + ... |Sn − 3 ∩ Sn − 2 ∩ Sn − 1 ∩ Sn|)
  ......
  + (−1)^(n − 1) |S1 ∩ S2 ∩ ... Sn − 1 ∩ Sn|

或者这样表示：

扩展问题：

Number of permutations of the multiset {1,1,2,2,....,n,n} with no two consecutive terms equal.

    当n从1开始，依据上面的方法所得结果依次会是，0, 2, 30, 864, 39480, 2631600, 241133760, 29083420800, 4467125013120, 851371260364800, 197158144895712000, 54528028997584665600, 17752366094818747392000, 6720318485119046923315200, 2927066537906697348594432000, 1453437879238150456164433920000。