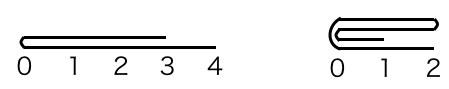【Codeforces Round 263 (Div 2)E】【坐标映射 脑洞】Appleman and a Sheet of Paper 折纸游戏 区间查询
Appleman and a Sheet of Paper
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
Appleman has a very big sheet of paper. This sheet has a form of rectangle with dimensions 1 × n. Your task is help Appleman with folding of such a sheet. Actually, you need to perform q queries. Each query will have one of the following types:
- Fold the sheet of paper at position pi. After this query the leftmost part of the paper with dimensions 1 × pi must be above the rightmost part of the paper with dimensions 1 × ([current width of sheet] - pi).
- Count what is the total width of the paper pieces, if we will make two described later cuts and consider only the pieces between the cuts. We will make one cut at distance li from the left border of the current sheet of paper and the other at distance ri from the left border of the current sheet of paper.
Please look at the explanation of the first test example for better understanding of the problem.
Input
The first line contains two integers: n and q (1 ≤ n ≤ 105; 1 ≤ q ≤ 105) — the width of the paper and the number of queries.
Each of the following q lines contains one of the described queries in the following format:
- "1 pi" (1 ≤ pi < [current width of sheet]) — the first type query.
- "2 li ri" (0 ≤ li < ri ≤ [current width of sheet]) — the second type query.
Output
For each query of the second type, output the answer.
Examples
input
7 4 1 3 1 2 2 0 1 2 1 2
output
4 3
input
10 9 2 2 9 1 1 2 0 1 1 8 2 0 8 1 2 2 1 3 1 4 2 2 4
output
7 2 10 4 5
Note
The pictures below show the shapes of the paper during the queries of the first example:
After the first fold operation the sheet has width equal to 4, after the second one the width of the sheet equals to 2.
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 1e5+10, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, q;
int o, p, l, r;
int a[N];
int s[N];
int L, R; bool flip;
void init()
{
L = 1; R = n;
for (int i = 1; i <= n; ++i)
{
a[i] = 1;
s[i] = s[i - 1] + a[i];
}
flip = 0;
}
void solve()
{
while (q--)
{
scanf("%d", &o);
if (o == 1)
{
int len = R - L + 1;
scanf("%d", &p);
if (!flip)
{
//翻转部分更少，我们进行翻转
if (p <= len - p)
{
int l = L + p;
int r = L + p + p - 1;
int U = l + l - 1;
s[l - 1] = 0;
for (int i = l; i <= r; ++i)
{
a[i] += a[U - i];
s[i] = s[i - 1] + a[i];
}
L += p;
}
//不翻转部分更少，我们反向操作
else
{
p = len - p;
int l = R - p - p + 1;
int r = R - p;
int U = r + r + 1;
for (int i = l; i <= r; ++i)
{
a[i] += a[U - i];
s[i] = s[i - 1] + a[i];
}
R -= p;
flip = 1;
}
}
else
{
//翻转部分更少，我们进行翻转
if (p <= len - p)
{
int l = R - p - p + 1;
int r = R - p;
int U = r + r + 1;
for (int i = l; i <= r; ++i)
{
a[i] += a[U - i];
s[i] = s[i - 1] + a[i];
}
R -= p;
}
//不翻转部分更少，我们反向操作
else
{
p = len - p;
int l = L + p;
int r = L + p + p - 1;
int U = l + l - 1;
s[l - 1] = 0;
for (int i = l; i <= r; ++i)
{
a[i] += a[U - i];
s[i] = s[i - 1] + a[i];
}
L += p;
flip = 0;
}
}
}
else
{
scanf("%d%d", &l, &r); --r;
int ans;
if (!flip)ans = s[L + r] - s[L + l - 1];
else ans = s[R - l] - s[R - r - 1];
printf("%d\n", ans);
}
}
}
int main()
{
while (~scanf("%d%d", &n, &q))
{
init();
solve();
}
return 0;
}
/*
【trick&&吐槽】
CFdiv2E并不一定很难。毕竟诗诗都想出来怎么做了233>_<
【题意】
给你一张1*n（1e5）的纸条，纸条上有0~n共计n个刻度。
我们有q（1e5）个操作。
对于每个操作，有两种类型：
(1,pi)，表示我们把纸条的[0,pi]向右翻转。
(2,l,r)，表示我们查询l~r区间段有多少个纸条单位
【类型】
复杂度分析 坐标映射
【分析】
其实，我们每次只要翻转较小的一侧就好了。
唯一需要处理的是坐标映射。
我们只要记录一个实际区间，同时记录flip表示是否翻转过。
如果未翻转过，操作从从左往右翻转，从左往右查询。
如果翻转过，操作从右向左翻转，从右向左查询
【时间复杂度&&优化】
总翻转长度不会超过n，复杂度为O(n)
【数据】
10 100
1 9
2 0 1
2 0 2
2 0 3
2 0 9
*/