Java集合框架面试问题集锦
Q:最常见的数据结构有哪些,在哪些场景下应用它们?
A. 大部分人都会遗漏树和图这两种数据结构。树和图都是很有用的数据结构。如果你在回答中提及到它们的话,面试者可能会对你进行进一步进行的考核。
Q:你如何自己实现List,Set和Map?
A:虽然Java已经提供了这些接口的经过实践证明和测试过的实现,但是面试者还是喜欢这样问,来测试你对数据结构的理解。我写的《Core Java Career Essentials》一书中通过图例和代码详细地讲解了这些内容。
常见的数据结构
数组是最常用的数据结构。数组的特点是长度固定,可以用下标索引,并且所有的元素的类型都是一致的。数组常用的场景有把:从数据库里读取雇员的信息存储为EmployeeDetail[],把一个字符串转换并存储到一个字节数组中便于操作和处理,等等。尽量把数组封装在一个类里,防止数据被错误的操作弄乱。另外,这一点也适合其他的数据结构。
列表和数组很相似,只不过它的大小可以改变。列表一般都是通过一个固定大小的数组来实现的,并且会在需要的时候自动调整大小。列表里可以包含重复的元素。常用的场景有,添加一行新的项到订单列表里,把所有过期的商品移出商品列表,等等。一般会把列表初始化成一个合适的大小,以减少调整大小的次数。
集合和列表很相似,不过它不能放重复的元素。当你需要存储不同的元素时,你可以使用集合。
堆栈只允许对最后插入的元素进行操作(也就是后进先出,Last In First Out – LIFO)。如果你移除了栈顶的元素,那么你可以操作倒数第二个元素,依次类推。这种后进先出的方式是通过仅有的peek(),push()和pop()这几个方法的强制性限制达到的。这种结构在很多场景下都非常实用,例如解析像(4+2)*3这样的数学表达式,把源码中的方法和异常按照他们出现的顺序放到堆栈中,检查你的代码看看小括号和花括号是不是匹配的,等等。
这种用堆栈来实现的后进先出(LIFO)的机制在很多地方都非常实用。例如,表达式求值和语法解析,校验和解析XML,文本编辑器里的撤销动作,浏览器里的浏览记录,等等。这里是一些关于堆栈的一些Java面试题。
队列和堆栈有些相似,不同之处在于在队列里第一个插入的元素也是第一个被删除的元素(即是先进先出)。这种先进先出的结构是通过只提供peek(),offer()和poll()这几个方法来访问数据进行限制来达到的。例如,排队等待公交车,银行或者超市里的等待列队等等,都是可以用队列来表示。
这里是一个用多线程来访问阻塞队列的例子。
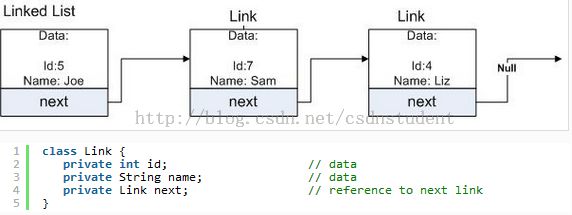
链表是一种由多个节点组成的数据结构,并且每个节点包含有数据以及指向下一个节点的引用,在双向链表里,还会有一个指向前一个节点的引用。例如,可以用单向链表和双向链表来实现堆栈和队列,因为链表的两端都是可以进行插入和删除的动作的。当然,也会有在链表的中间频繁插入和删除节点的场景。Apache的类库里提供了一个TreeList的实现,它是链表的一个很好的替代,因为它只多占用了一点内存,但是性能比链表好很多。也就是说,从这点来看链表其实不是一个很好的选择。
ArrayList是列表的一个很好的实现。相比较TreeList而言,ArrayList在除了在列表中间插入或者删除元素的情况,其他操作都比TreeList快很多。TreeList的实现是在内部使用了一个树形的结构来保证所有的插入和删除动作的复杂度都是O(log n)的。这种实现方式使得TreeList在频繁插入和删除元素的时候的性能远远高于ArrayList和LinkedList。
HashMap的访问时间接近稳定,它是一种键值对映射的数据结构。这个数据结构是通过数组来实现的。它通过hash函数来给元素定位,并且用冲突检测算法来处理被hash到同一位置的值。例如,保存雇员的信息可以用雇员的id来作为key,对从properties文件里读入的属性-属性值可以用key/value对来保存,等等。HashMap在初始化的时候,给定一个合适的大小可以减少调整大小的次数。
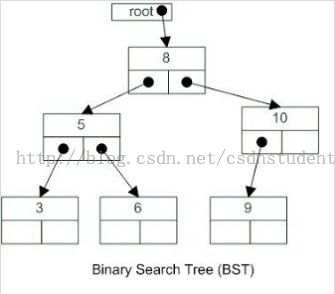
树是一种由节点组成的数据结构,每个节点都包含数据元素,并且有一个或多个子节点,每个子节点指向一个父节点(译者注:除了根节点)可以表示层级关系或者数据元素的顺序关系。常用的场景有表示一个组织里的雇员层级关系,XML元素的层级关系,等等。如果树的每个子节点最多有两个叶子节点,那么这种树被称为二叉树。二叉树是一种非常常用的树形结构, 因为它的这种结构使得节点的插入和删除都非常高效。树的边表示从一个节点到另外一个节点的快捷路径。
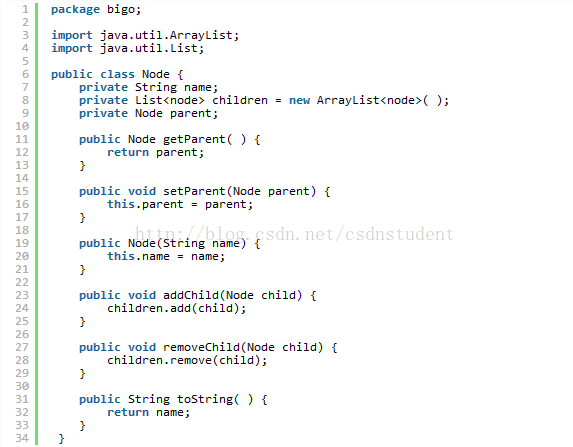
Java里面没有直接提供树的实现,但是它很容易通过下面的方式来实现。只需要创建一个Node对象,里面包含一个指向叶子节点的ArrayList。
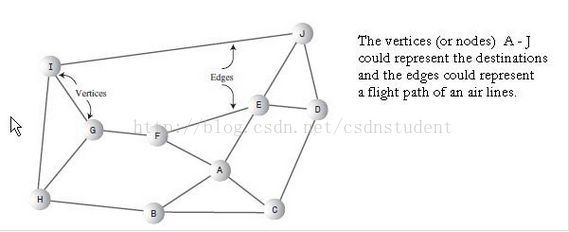
只要数据元素的关系可以表示成节点和边的网状结构的话,就可以用图来表示。树是一种特殊的图,它的所有节点都只能有一个父节点。和树不同的是,图的形状是由实际问题或者问题的抽象来决定的。例如,图中节点(或者顶点)可以表示不同的城市,而图的边则可以表示两个城市之间的航线。
在Java里构造一个图,你需要解决数据通过什么方式保存和访问的问题。在图里面也会用到上面提到的数据结构。Java的API里没有提供图的实现。不过有很多第三方库里提供了,例如JUNG,JGraphT,以及JDSL(不过好像不支持泛型)。《Core Java Career Essential》一书包含了用Java实现的可用示例。
Q:你对大O这个符号有什么了解呢,你是否可以根据不同的数据结构举出一些列子来?
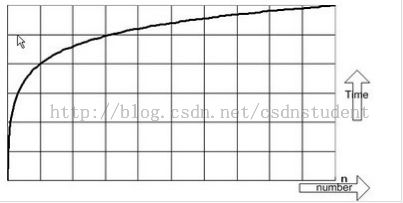
A:大O符号可以表示一个算法的效率,也可以用来描述当数据元素增加时,最坏情况下的算法的性能。大O符号也可以用来衡量的性能,例如内存消耗量。有时候你可能会为了减少内存使用量而选择一个比较慢的算法。大O符号可以表示在大量数据的情况下程序的性能。不过,对于程序在大量数据量下的性能的测量,唯一比较实际的方式是行用较大的数据集来进行性能基准测试,这样可以把一些在大O复杂度分析里没有考虑到的情况包含进去,例如在虚拟内存使用比较多的时候系统会发生换页的情况。虽然基准测试比大O符号表示的结果更加实际,但是它不适用于设计阶段,所以在这个这时候大O复杂度分析是最合适的选择。
各种数据结构在搜索,插入和删除算法上的性能都可以用下面方式表示:常量复杂度O(1),线性复杂度O(n),对数复杂度O(log n),指数复杂度O(c^n),多项式复杂度O(n^c),平方复杂度O(n^2)以及阶乘复杂度O(n!),这里面的n都指的是数据结构里的元素的数量。性能和内存占用是可以相互权衡的。下面是一些示例。
示例1:在HashMap里查找一个元素的的时间复杂度是常量的,也即是O(1)。这是因为查找元素使用的是哈希函数,并且计算一个哈希值的时间是不受HashMap里的元素的个数的影响的。
示例2:线性搜索一个数组,列表以及链表都是的复杂度线性的,也即是O(n),这是查找的时候需要遍历整个列表。也就是说,如果一个列表的长度是原来的两倍,那么搜索所花的时间也是原来的两倍。
示例3:一个需要比较数组里的所有元素的排序算法的复杂度是多项式的,即是O(n^2)。这是因为一个嵌套的for循环的复杂度是O(n^2)。在搜素算法里有这样的例子。
示例4:二分搜索一个数组或者数组列表的复杂度是对数的,即是O(log n)。在链表里查询一个节点的复杂度一般是O(n)。相比较数组链表和数组的O(log n)的性能而言,随着元素数量的增长,链表的O(n)的复杂度的性能就比较差了。对数的时间复杂度就是如果10个元素花费的时间是x单位的话,100个元素最多花费2x单位的时间,而10000个元素最多花费4x个单位的时间。如果你在一个平面坐标上画出图形的话,你会发现时间的增长没有n(元素的个数)快。
Q:HashMap和TreeMap在性能上有什么样的差别呢?你比较倾向于使用哪一个?
A:一个平衡树的性能是O(logn)。Java里的TreeMap用一个红黑树来保证key/value的排序。红黑树是平衡二叉树。保证二叉树的平衡性,使得插入,删除和查找都比较快,时间复杂度都是O(log n)。不过它没有HashMap快,HashMap的时间复杂度是O(1),但是TreeMap的优点在于它里面键值是排过序的,这样就提供了一些其他的很有用的功能。
Q:怎么去选择该使用哪一个呢?
A:使用无序的HashSet和HashMap,还是使用有序的TreeSet和TreeMap,主要取决于你的实际使用场景,一定程度上还和数据的大小以及运行环境有关。比较实际的一个原因是,如果插入和更新都比较频繁的话,那么保证元素的有序可以提高快速和频繁查找的性能。如果对于排序操作(例如产生一个报表合作者运行一个批处理程序)的要求不是很频繁的话,那么把数据以无序的方式存储,然后在需要排序的时候用Collections.sort(…)来进行排序,会比用有序的方式来存储可能会更加高效。这个只是一种可选的方式,没人能给你一个确切的答案。即使是复杂度的理论,例如O(n),成立的前提也是在n足够大的情况下。只要在n足够小的情况下,就算是O(n)的算法也可能会比O(log n)的算法更加高效。另外,一个算法可能在AMD处理器上的速度比在Intel处理器上快。如果你的系统有交换区的话,那么你还要考虑磁盘的性能。唯一可以确定的性能测试途径是用大小合适的数据来测试和衡量程序的性能和内存使用量。在你所选择的硬件上来测试这两种指标,是最合适的方法。
Q:如何权衡是用无序的数组还是有序的数组呢?
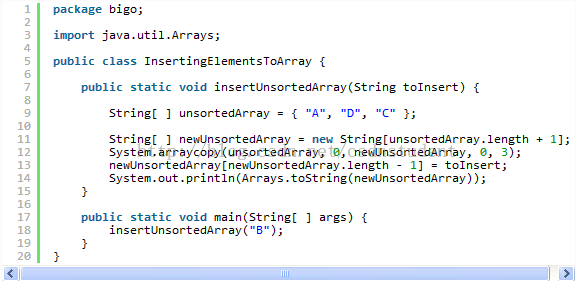
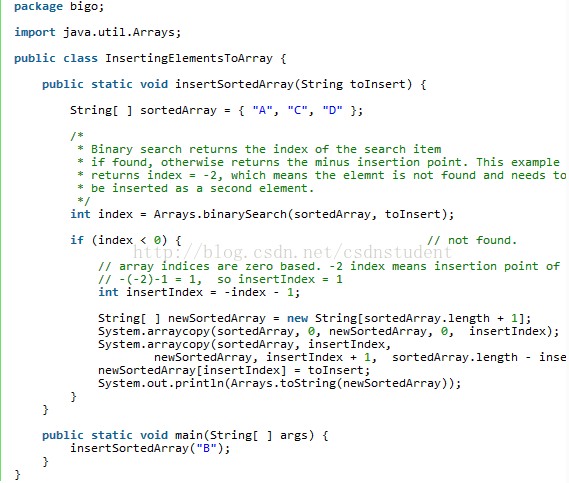
A:有序数组最大的优点在于n比较大的时候,搜索元素所花的时间O(log n)比无序素组所需要的时间O(n)要少很多。有序数组的缺点在于插入的时间开销比较大(一般是O(n)),因为所有比插入元素大的值都要往后移动。而无序数组的插入时间开销是常量时间,也就是说,插入的速度和元素的数量无关。下面的代码片段展示了向有序数组和无序数组插入元素。
插入元素到一个无序的数组里
所以,如何去选择还是取决于实际的使用情况。你需要考虑下面几个问题。你的程序是插入/删除的操作多,还是查找的操作多?数组里最多可能存储多少元素?排序的频率是多少?以及你的性能基准测试的结果是怎样的?
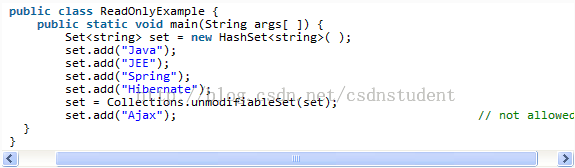
Q:怎么实现一个不可变集合?
A:这个功能在Collections类里实现了,它通过装饰模式实现了对一般集合的封装。
Q:怎么实现一个不可变集合?
A:这个功能在Collections类里实现了,它通过装饰模式实现了对一般集合的封装。
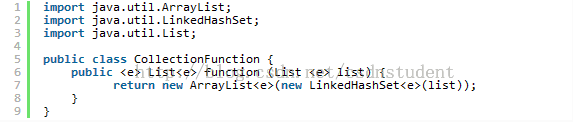
Q:下面的代码的功能是什么呢?其中的LinkedHashSet能用HashSet来取代吗?
A:上面的代码代码通过把原有列表传入一个LinkedHashSet来去除重复的元素。在这个情况里,LinkedHashSet可以保持元素原来的顺序。如果这个顺序是不需要的话,那么上面的LinkedHashSet可以用HashSet来替换。
Q:Java集合框架都有哪些最佳实践呢?
A:根据实际的使用情况选择合适的数据结构,例如固定大小的还是需要增加大小的,有重复元素的还是没有的,需要保持有序还是不需要,遍历是正向的还是双向的,插入是在末尾的还是任意位置的,更多的插入还是更多的读取,是否需要并行访问,是否允许修改,元素类型是相同的还是不同的,等等。另外,还需要尽早考虑多线程,原子性,内存使用量以及性能等因素。
不要假设你的集合里元素的数量一直会保持较小,它也有可能随着时间增长。所以,你的集合最好能够给定一个合适的大小。
针对接口编程优于针对实现编程。例如,可能在某些情况下,LinkedList是最佳的选择,但是后来ArrayList可能因为性能的原因变得更加合适
不好的方式 : ![]()
好的方式:
在取得列表的时候,如果返回的结果是空的话,最好返回一个长度为0的集合或者数组,而不要返回null。因为,返回null的话可能能会导致程序错误。调用你的方法的开发人员可能会忘记对返回为null的情况进行处理。
封装好集合:一般来说,集合都是不可变的对象。所以尽量不要把集合的成员变量暴露给调用者。因为他们的操作一般都不会进行必要的校验。
注:这些Java面试题和答案都是从我的书《Core Java Career Essentials》里提取出来的。
英文原文:java-success,编译:ImportNew - 朱伟杰
译文地址: http://www.importnew.com/871.html