pku1430（第二类Stirling数 Sierpinski三角形）

http://162.105.81.212/JudgeOnline/problem?id=1430

此题是求第二类Stirling数S(n,k)的值，但是n,k的范围非常大；下面是有关的资料，转帖的；

 

 

 

首先介绍一下Sierpinski三角形：

       Sierpinski三角形是一种分形图形，它是递归地构造的。最常见的构造方法如上图所示：把一个三角形分成四等份，挖掉中间那一份，然后继续对另外三个三角形进行这样的操作，并且无限地递归下去。每一次迭代后整个图形的面积都会减小到原来的3/4，因此最终得到的图形面积显然为0。

       Sierpinski三角形的另一种构造方法如下图所示。把正方形分成四等份，去掉右下角的那一份，并且对另外三个正方形递归地操作下去。挖个几次后把脑袋一歪，你就可以看到一个等腰直角的Sierpinski三角形。

        Sierpinski三角形&杨辉三角：

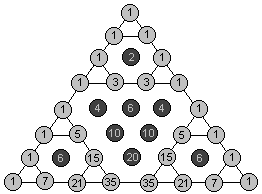
         当我在Matrix67博客里看到这个时真的感觉相当神奇，相当完美，太不可思议了。我们写出8行或16行的杨辉三角，然后把其中的奇数和偶数标上不同的颜色，会发现杨辉三角（模2）与Sierpinski三角形时等价的。也就是二项式系数（组合数）的奇偶性竟然是个分型图形。

        

       我们仔细观察一下就可以发现通过杨辉三角奇偶表的前四行可以推出后四行来。可以看到杨辉三角的前四行是一个二阶的Sierpinski三角形，它的第四行全是奇数。由于奇数加奇数等于偶数，那么第五行中除了首尾两项为1外其余项都是偶数。而偶数加偶数还是偶数，因此中间那一排连续的偶数不断地两两相加必然得到一个全是偶数项的“倒三角”。同时，第五行首尾的两个1将分别产生两个和杨辉三角前四行一样的二阶Sierpinski三角形。这正好组成了一个三阶的Sierpinski三角形。显然它的最末行仍然均为奇数，那么对于更大规模的杨辉三角，结论将继续成立。

        Sierpinski三角形与位运算

         先提供一个程序可以输出Sierpinski三角形。

#include <stdlib.h> #include <stdio.h> int main(int argc, char** argv) { int i,j,n=(1<<5)-1; for (i=0;i<=n;i++) { for (j=0;j<=n;j++) printf((i&j)==j ? "#":" "); printf("/n"); } return (EXIT_SUCCESS); } 

 

输出为：

这个程序告诉我们：在第i行第j列上打一个点当且仅当i and j=j，这样最后得到的图形就是一个Sierpinski三角形。这是为什么呢？其实原因很简单。把i和j写成二进制（添加前导0使它们位数相同），由于j不能大于i，因此只有下面三种情况：
     情况一：
     i = 1?????
     j = 1?????
     问号部分i大于等于j
     i的问号部分记作i'，j的问号部分记作j'。此时i and j=j当且仅当i' and j'=j'

     情况二：
     i = 1?????
     j = 0?????
     问号部分i大于等于j
     i的问号部分记作i'，j的问号部分记作j'。此时i and j=j当且仅当i' and j'=j'

     情况三：
     i = 1?????
     j = 0?????
     问号部分i小于j
     此时i and j永远不可能等于j。i' < j'意味着i'和j'中首次出现数字不同的那一位上前者为0，后者为1，那么i和j做and运算时这一位的结果是0，与j不等。
     注意到，去掉一个二进制数最高位上的“1”，相当于从这个数中减去不超过它的最大的2的幂。观察每一种情况中i,j和i',j'的实际位置，不难发现这三种情况递归地定义出了整个Sierpinski三角形。
     嘿！发现没有，通过Sierpinski三角形证明了这个结论：组合数C(N,K)为奇数当且仅当N and K=K。

在维基百科上关于第二类Stirling数的介绍中有这样一个公式：

        s（n，k）=c（z，w）（mod 2）

        z=n-ceil（（k+1）/2）;   w=floor（（k-1）/2）;

根据第二类Stirling数的递推公式 s（n，k）=k*s（n-1，k）+s（n-1，k-1）；分k为奇数和偶数的情况推一下就可以了，首先由于%2的操作，我想到了f(n,k) = s(n,k)%2，假设一个f函数。于是s(n,k) = k* s(n-1,k)+ s(n-1,k-1) ==>f(n,k) = s(n-1,k-1) (k为偶数); f(n,k) = f(n-1,k) + f(n-1,k-1)（k为奇数）。这样就可以将k给去掉，最后就是计算f(n,k)%2即可，必须想到怎么样得到f(n,k)。也就是f(n,k)=c(n,k)%2。

首先根据n，k求出z，w，再判断（z&w）是否等于w就可以了。

但是自己看完也想了很久还是云里雾里的……

#include<iostream> using namespace std; int main() //维基百科上面的公式s(n,k)=c(z,w)%2; c(z,w)表示组合数运算, { //z= n - ceil((k+1)/2); w= floor((k-1)/2); int t,n,k,z,w; scanf("%d",&t); while(t-- && scanf("%d%d",&n,&k)) { w = (k-1)/2; //求的是floor((k-1)/2)的值，就是向下取整； z = n - k + w; //求的是n - ceil((k+1)/2)的值，就是向上取整； //cout<<w<<" "<<z<<endl; if((z & w) == w) printf("1/n"); else printf("0/n"); } return 0; }