图算法 图的表示(邻接表和邻接矩阵)和拓扑排序
图的表示
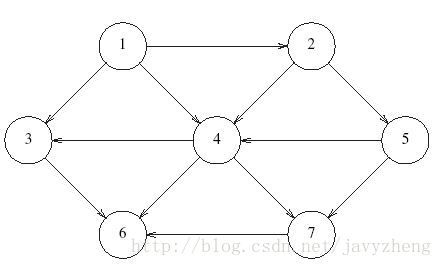
图有两种表示方法,分别是邻接矩阵和邻接表。这里以有向图为例说明。
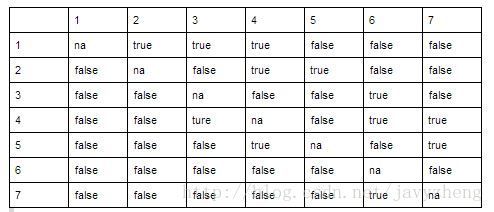
邻接矩阵
邻接矩阵是一个二维数组A。对于每条边 (u,v),置A[u][v]等于true;否则,数组元素为false。
如果边有一个权,那么可以置A[u][v]等于该权,而使用一个很大或者很小的权作为标记表示不存在的边。
它的空间需求为Θ(|V|^2)。
邻接表
大多数情况,图都是比较稀疏的,那么用邻接表表示更为合适。
对每一个顶点,使用一个表存放所有邻接的顶点。这样的空间需求为Θ( |E| + |V| )。
邻接表是图的标准表示方法。可以为每个顶点数据结构增加一个邻接表域才存储这个表。
拓扑排序
拓扑排序是对有向无圈图顶点的一种排序,是的如果存在一条从vi到vj的路径,那么在排序中vj就出现在vi后面。注意:只保证先后顺序,不保证相邻顶点挨着出现。
做法是:对每个顶点,除了保持邻接表,还有入度(indegree,定义为边(u,v)的条数),拓扑编号(topNum)。
使用一个队列存储入度为0的顶点。
1,对每个顶点计算它的入度,将所有入度为0的顶点放在一个初始为空的队列;
2,当队列不空时,删除一个顶点v,并将于v邻接的所有顶点的入度减1。
3,只要一个顶点的入度降为0,就将该顶点放入队列中。
4,此时,拓扑排序就是顶点入队的顺序。
//伪代码,可以很方便改写为Java代码
void topsort( ){
//哪个队列实现类的都可以
Queue<Vertex> q = new Queue<Vertex>( );
int counter = 0;
for each Vertex v
if( v.indegree == 0 )
q.enqueue( v );
while( !q.isEmpty( ) ){
Vertex v = q.dequeue( );
v.topNum = ++counter;
for each Vertex w adjacent to v
if( --w.indegree == 0 )
q.enqueue( w );
}
if( counter != NUM_VERTICES )
print("Circle exists!");
}