一种可扩展的表达式解析及计算方法
概述
在应用软件开发领域,对表达式计算的应用有非常广泛的应用。例如,在报表开发中,经常为用户提供公式输入功能,从而实现更灵活的报表汇总;工作流应用软件中,经常利用逻辑条件进行动态配置,从而提供更加灵活的流程配置;另外,在某些 UI 开发中,需要通过某个属性的表达式计算结果来动态控制 UI 组件的显示。所有这些应用都可以归结为一个通用模型,即表达式的解析以及计算。本文旨在提供一种可扩展的表达式解析及其计算方法。
表达式解析的一般条件及因素
本文所讲的表达式是一种以一定的运算规则组合所表达的字符串;另外,通过解析表达式字符串并以其代表的运算规则可以得到一个结果。表达式解析一般需要满足下列条件:
- 支持的操作符集合
- 操作符的优先级
- 操作符所代表的操作规则集合
- 支持的分隔符集合以及分隔符所代表的意义
- 支持的数据类型集合
- 语法约束,如命名规则、分割符所代表的语法规则等
表达式解析除了以上必须满足的条件之外,在有些表达式环境中,可能还支持函数、变量。结合本文所要解决的问题,如下列出可选的条件:
- 支持的内部函数集合
- 支持的内部全局变量
- 支持函数定制
- 支持自定义变量
- 支持函数以及操作符重载
以上最后三个可选条件,是一个表达式解析引擎的可扩展支持需要满足的条件。
回页首
再谈编译原理
一般的编译过程主要包括词法分析、语法分析、语义分析、中间代码生成、代码优化、目标代码生成,如下图所示。其中,词法分析主要任务是输入源程序,对构成源程序的程序进行扫描和分解,识别出一个一个的单词。单词是语言中具有独立意义的最基本结构。一般这些单词包括程序语言所支持的保留字、数据类型、操作符、分隔符以及程序定义的标识符、常量等。
语法分析的主要任务是在词法分析的基础上,根据语言的语法规则把单词序列组合成各类语法单位(一般表示成语法树)。
语义分析的主要任务是进一步分析语法结构正确的程序是否符合源程序的上下文约束、运算相容性等语义约束规则。
图 1. 编译一般过程
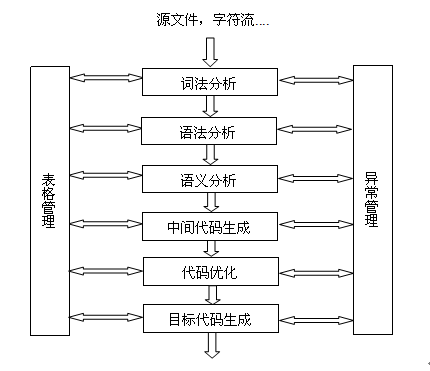
上述只是非常简要的介绍了一般的编译原理知识,详细知识需要参考编译原理相关的书籍和文档。对于本文所讲的表达式解析,笔者认为其与程序编译具有本质上的相似,只是在问题的复杂性上会简单的很多。表达式解析同样需要首先把输入的表达式字符串分解成一个一个的单词,然后把单词序列组合成语法单位,最后依据表达式的语言环境所定义的语义约束对这些语法单位进行分析计算。因此,我们可以程序编译的基本方法有选择的运用到表达式解析上。
回页首
中缀表达式、前缀表达式、后缀表达式
前缀表达式(又叫波兰式)是一种不含括号的 表达式,并且将 运算符放在 操作数前面的表达式。对于一个前缀表达式的求值而言,所有的计算按运算符出现的顺序,严格从左向右进行。
后缀表达式(又叫逆波兰式)也是一种不含括号的 表达式,并且 运算符放在操作数的后。对于一个后缀表达式的求值而言,所有的计算按运算符出现的顺序,严格从左向右进行。
中缀表达式是一个通用的算术或逻辑公式表示方法, 操作符是以中缀形式处于操作数的中间。中缀表达式不容易被计算机解析,但它符合人们的普遍用法。与前缀或后缀记法不同的是,中缀记法中括号是必需的。计算过程中必须用括号将操作符和对应的操作数括起来,用于指示运算的次序。
前缀表达式和后缀表达式是一种十分有用的表达式,它可以依靠简单的操作就能得到运算结果的表达式。通常解析程序一般都会将中缀表达式转换为前缀表达式或后缀表达式,方便表达式计算。
回页首
表达式树
前面讲过,表达式是一种以一定的运算规则组合所表达的字符串。每一个表达式的基本组成单位都是由一个操作符和操作数组成的操作单位,操作数可以是一个或者多个。所以一个表达式基本操作单位可以表示为一棵树,下图所示为一个N元操作符的树表示,该操作符代表的运算需要N个操作数:
图 2. N元操作符的树表示
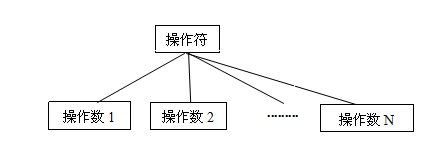
每个基本操作单位可以表示为一棵树,每个操作单位的运算结果为其它操作符的一个操作数,从而一个含有多个操作符的表达式可以表示成一棵更大的树,其每一棵子树皆为一个子表达式。如表达式 a*b+c/d 可以表示为:
图 3. 表达式 a*b+c/d 的树表示
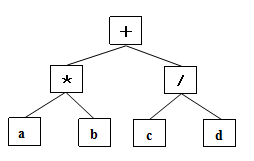
从编译原理的知识可以得出这样一个结论,一个表达式可能推导出多棵树,呈现出二义性。因此,需要通过对表达式的语言环境增加语义约束规则,消除二义性,保证从表达式只能推导出唯一的表达式树。通常的语义约束规则包括设定操作符的优先级、括号的使用等。
回页首
表达式解析引擎的基本结构设计
图 4. 解析引擎的基本结构设计( 查看大图)
如 图 4 所示,展示了一个表达式解析引擎的基本结构设计。整个表达式解析引擎内部结构主要包括:表达式解析引擎的语言环境定义、操作符处理器管理、表管理器、表达式解析器、表达式校验器、表达式解析异常定义等。本文后续部分将详细解释。
回页首
表达式解析引擎实现说明
定义表达式解析引擎的语言环境
对于表达式解析,首先必须定义表达式所存在的语言环境。主要包括表达式所支持的数据操作、数据类型、合法的操作符集合、保留字、分隔符等。另外还包括内部自定义并可供表达式引用的全局变量、函数等。所有这些语言环境因素都通过表格管理器进行统一管理,如 图 4 所示 TableManger 类。
表格管理器主要用于符号管理,主要管理如下四类符号数据:
操作符管理
操作符管理主要管理表达式所支持的所有操作符,包括内置操作符以及用户自定义的操作符。其中,用户自定义的操作符属于表达式解析引擎中可扩展特性,需要注册到表格管理器,以便表达式引用。
操作符具备一般的符号特性,包括操作符标示字符串,操作数以及操作数个数。另外,不同的操作符具有不同的操作优先级。
语法保留字管理
语法保留字管理主要存储表达式所支持的各种关键字、分隔符等,属于表达式构成的一部分。如"("、")"、","、"const"、"var"等。
函数管理
函数管理主要管理表达式所支持的所有函数,包括内置函数以及用户自定义的函数。其中,用户自定义的函数属于表达式解析引擎中可扩展特性,需要注册到表格管理器,以便表达式引用。
变量管理
变量管理主要管理表达式解析引擎内置的全局变量以及用户自定义的变量。其中,用户自定义的变量属于表达式解析引擎中可扩展特性,需要注册到表格管理器,以便表达式引用。
对于表格管理中的可扩展特性将在本文稍后部分讲解。下面给出符号定义结构示例:
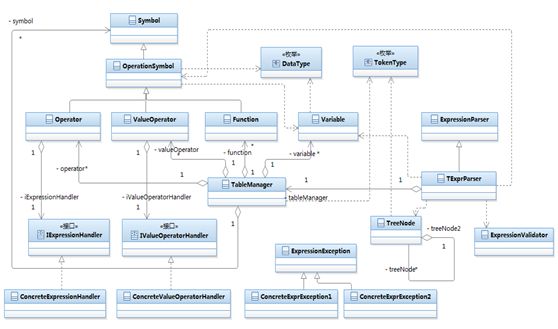
图 5. 符号定义结构( 查看大图)
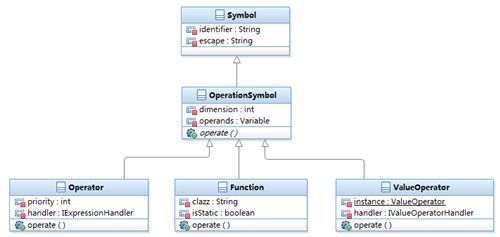
Symbol 类定义了表格管理中一般性符号,包括标识字符串 identifier 和转义字符串 escape 两个属性。
OperationSymbol 类定义了一般性的操作符号,包括操作数个数 dimension 以及操作数集合 operands。前面讲过,表达式中任何操作都可以抽象归纳为操作符以及零或多个操作数两部分。本文涉及的操作主要包括基本操作符,函数以及取值符所代表的操作。当然,操作数包括数据类型、数据值等属性,用 Variable 类型的对象表示。
需要注意的是,任何一个表达式一般都是一个字符串。所以,表达式解析过程需要正确解析字符串表达式中各个操作数的数据类型。
Operator 类定义了表达式解析引擎中基本的操作符号,如 +、—、*、/、&&、|| 等。Operator 类包括操作符优先级 priority 以及操作处理器 handler。
Function 类代表函数,包括函数实现类 clazz 属性以及用于判断函数是否静态的 isStatic 属性。
ValueOperator 类定义了表达式中的取值操作符。因为一个解析引擎通常仅仅只有一个取值操作符,所以该类属于一个单例模型,包括一个 ValueOperator 对象实例属性以及取值操作符处理器 handler。
本节阐述了表格管理器的内容,以下 清单 1 所示给出一个表格管理器示例,简要列出表格管理器属性及操作。
清单 1. 表格管理器
public class TableManager {
// 管理 / 存储表达式语言环境涉及的操作符,包括解析引擎保留操作符以及用户注册的自定义操作符
private static Hashtable<String, Operator>
tblOperator = new Hashtable<String, Operator>();
// 管理 / 存储表达式语言环境涉及的语法关键字
private static Hashtable<String, Symbol>
tblSyntaxKey = new Hashtable<String, Symbol>();
// 管理 / 存储表达式语言环境定义的函数,包括解析引擎内部函数以及用户注册的自定义函数
private static Hashtable<String, Function>
tblFunction = new Hashtable<String, Function>();
// 管理 / 存储表达式语言环境定义的变量,包括解析引擎内部全局变量以及用户注册的自定义变量
private static Hashtable<String, Variable>
tblGlobalVar = new Hashtable<String, Variable>();
// 标示符最大长度,方便表达式解析过程中的回朔处理
private static int MAX_IDENTIFIER_LEN = 1;
// 操作符是否可被重写处理器
private static boolean isOverridable = false;
// 根据标示符号字符串取得操作符
public static Operator getOperator(String identifier) {
// 省略代码 ....
}
// 根据标示符号字符串取得函数
public static Function getFunction(String identifier) {
// 省略代码 ....
}
// 根据标示符号字符串取得标示符
public static Symbol getIdentifier(String identifier) {
// 省略代码 ....
// 注册操作符
public static boolean regOperator(Operator oper) {
// 省略代码 ....
}
// 注册语法关键字
public static boolean regSyntaxKeys(Symbol identifier) {
// 省略代码 ....
}
// 注册函数
public static boolean regFunction(Function func) {
// 省略代码 ....
}
// 判断是否存在某标示符
public static boolean existIdentifier(String identifier) {
// 省略代码 ....
}
// 判断是否存在某操作符
public static boolean existOperator(String identifier) {
// 省略代码 ....
}
// 判断是否存在某函数
public static boolean existFunc(String identifier) {
// 省略代码 ....
}
// 取得操作符优先级
public static int getPriority(String identifier) {
// 省略代码 ....
}
// 取得操作符定义的操作数个数
public static int getDimension(String identifier) {
// 省略代码 ....
}
// 取得最大标示符长度
public static int getMaxIdentifierLen() {
return MAX_IDENTIFIER_LEN;
}
// 取得单词类型
public static TokenType getTokenType(String token) {
// 省略代码 ....
}
// 判断是否为取值操作符
public static boolean isValueOperator(String token) {
// 省略代码 ....
}
// 根据变量名取得已注册的变量
public static Variable getVariable(String varName) {
// 省略代码 ....
}
// 判断是否存在某变量
public static boolean existVariable(String varName) {
// 省略代码 ....
}
// 注册变量
public static boolean regVariable(Variable var) {
// 省略代码 ....
}
}
|
操作符处理器以及可扩展的问题
在表达式解析过程中,除了正确解析出各种操作符以及操作数,还需要能依据这些操作符所代表的操作语义正确地进行数据的操作处理。 在本文的"表达式解析的一般条件及因素"部分,提出了三个可选条件作为解析引擎的扩展支持,从而增强解析引擎的功能。本文所提出的设计方案主要采用 Bridge 设计模式和反射模式实现操作符处理以及扩展支持。
图 6. 操作符处理器及可扩展处理结构( 查看大图)
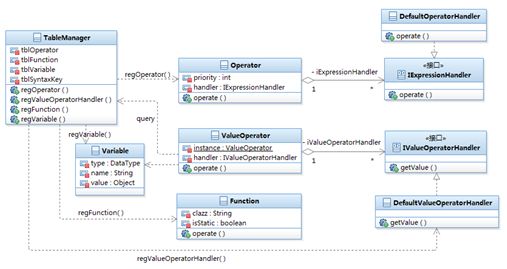
如 图 6 所示,提供了一个操作符处理器及可扩展处理的设计结构。组成表达式的操作单元主要包括基本操作符运算、变量取值、函数调用等。在 图 7 所示的结构中,表格管理器 TableManager 主要用于管理各种操作符、函数、变量等并以表的形式进行存储。至于表的实现,具体有很多种方法,如利用哈希表等。在基本操作符 Operator 和取值操作符 ValueOperator 的定义结构中,都定向聚集关联了一个操作处理器对象 handler。Operator 类的操作处理器类型为 IExpressionHandler 接口类型 , ValueOperator 类的操作处理器类型为 IValueOperatorHandler 接口类型。通过该设计方法,除了表达式解析引擎内部实现的缺省操作处理器,用户同样可以通过实现 IExpressionHandler 接口和 IValueOperatorHandler 接口,向表管理器 TableManager 中注册个性化业务相关的操作符处理以及取值处理。具体如下:
- 操作符处理:用户可以自定义操作符或者进行操作符重载。首先,用户通过实现 IExpressionHandler 接口实现用户第三方操作符处理;然后,定义或重载操作符对象,并且引用指向用户实现的第三方操作符处理器; 最后,通过 TableManager 提供的注册方法注册该操作符。
- 取值符处理:实现解析引擎内部的全局变量取值以及第三方业务相关的取值处理。对于全局变量的取值,首先需要注册自定义的全局变量,从而保证在表达式的计算过程中能通过查找表管理器 TableManager 中的全局变量表来获得变量的值。对于第三方业务相关的取值处理,首先需要实现 IValueOperatorHandler 接口来实现第三方取值处理,然后通过表管理器 TableManager 注册第三方处理器到取值符中(前面讲过,解析引擎通常仅仅只有一个取值操作符,所以单独注册取值处理器到取值操作符中)。
- 函数处理:实现解析引擎内部函数调用以及第三方自定义函数调用。函数处理主要通过在运行时状态下利用反射方法动态调用。表达式可利用的每个函数都需要通过表管理器 TableManager 注册到函数表中。在表达式解析计算过程中,当遇到函数调用时,函数处理器通过查询函数表得到函数相关信息,然后利用这些函数信息反射调用函数,从而得到函数的执行结果。
如 清单 2 所示,为一个加法处理器代码示例。该加法处理器能处理整型数字、浮点数以及字符串相加。
清单 2. 加法 + 操作符处理器
/**
* 加法操作符处理器,支持数值相加以及字符串相加
* @author Wang Jianguang
*/
public class PlusOperatorHandler implements IExpressionHandler {
/*
* 加法操作符处理器方法
* @param oper : 操作符号
* @return : Variable 类型的操作符处理结果
*/
public Variable operate(OperationSymbol oper) {
Variable res = null;
if(!validate(oper)) {
return res;
}
String identifier = oper.getIdentifier();
if(!identifier.equals("+")) {
return res;
}
Variable[] operands = oper.getOperands();
if(operands.length != 2) {
return res;
}
boolean isStrOp = containStrOperand(operands);
Object val0 = operands[0].getValue();
Object val1 = operands[1].getValue();
if(isStrOp) {
res = new Variable(DataType.STRING);
res.setValue(val0.toString() + val1.toString());
} else {
boolean isFloatResult = operands[0].getType() == DataType.FLOAT||
operands[1].getType() == DataType.FLOAT;
if(isFloatResult) {
float fvalue = Float.parseFloat(val0.toString())
+ Float.parseFloat(val1.toString());
res = new Variable(DataType.FLOAT);
res.setValue(fvalue);
} else {
int ivalue = Integer.parseInt(val0.toString())+
Integer.parseInt(val1.toString());
res = new Variable(DataType.INT);
res.setValue(ivalue);
}
}
return res;
}
|
表达式解析及计算方法
要正确解析表达式,首先必须通过词法分析能识别出表达式中一个一个的单词,这些单词包括基本操作符、关键字、分隔符和操作数,还可能包括函数、变量等。一般给定一个待计算的表达式,通常是符合某种语言环境所提供的语法结构;往往这种语法并不一定适合计算机内部计算,或者说,对计算机计算而言比较复杂。所有,对于表达式的分析与计算,通常需要把表达式转换为可以依靠简单的操作就能得到运算结果的表达式。前面讲过,通常解析程序一般都会将中缀表达式转换为前缀表达式或后缀表达式,方便表达式计算。本文正是将表达式转换为后缀表达式来进行分析与计算的。
图 7. 表达式解析与计算过程
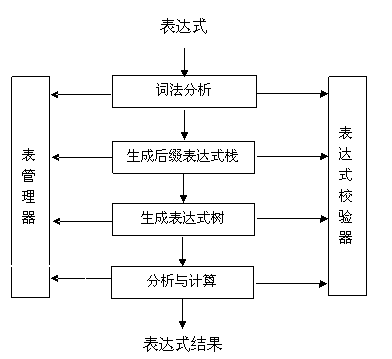
如 图 7 所示,展示了表达式的解析与计算过程。下面就该过程的每部分进行简要说明。
词法分析:识别出表达式中合法的单词,一般利用回朔算法进行分析,并利用表管理器来辅助识别。
生成后缀表达式栈:将表达式(一般为中缀表达式)转换为后缀表达式,并以栈结构进行存储,方便后续构造表达式树。
清单 3. 生成后缀表达式栈
/**
* 构造后缀表达式栈。通过词法分析,获得各种类别的单词,从而依据语法规则构造
* 后缀表达式栈
* @param expr 输入表达式
* @return 由各个单词构成的表达式栈
*/
public Stack<String> buildPostExpressionStack(String expr) {
Stack<String> retStack = new Stack<String>();
Stack<String> stack = new Stack<String>();
stack.push("ENDFLAG");
int iPointer = 0;
while(iPointer < expr.length()) {
// 词法分析,得到单词
String token = this.getToken(expr, iPointer);
int step = token.length();
if(token.equals("(")) {
stack.push(token);
} else if(TableManager.existOperator(token)) {
// 分析操作符
String lastToken = stack.lastElement();
while(TableManager.existFunc(lastToken)
|| TableManager.isValueOperator(token)
|| TableManager.getPriority(lastToken)
>= TableManager.getPriority(token)) {
retStack.push(stack.pop());
lastToken = stack.lastElement();
}
stack.push(token);
} else if(TableManager.existFunc(token) ||
TableManager.isValueOperator(token)) {
// 分析函数或取值符号
stack.push(token);
} else if(token.equals(",")) {
while(!stack.lastElement().equals("(")){
retStack.push(stack.pop());
}
} else if(token.equals(")")) {
while(!stack.lastElement().equals("(")) {
retStack.push(stack.pop());
}
stack.pop();
String lastToken = stack.lastElement();
if(TableManager.existFunc(lastToken)) {
retStack.push(stack.pop());
}
} else {
retStack.push(token);
}
iPointer += step;
}
while(!stack.lastElement().equals("ENDFLAG")) {
retStack.push(stack.pop());
}
adjust(retStack);
return retStack;
}
|
生成表达式树:前面讲过,一个含有多个操作符的表达式可以表示成一棵树。此过程正是利用此结论来构造一棵表达式树,方便后续的分析与计算结构。树的每个节点都保存每个操作符或操作数的相关信息。以树的结构存储表达式还方便扩展分析处理。如 清单 4 所示为生成表达式树代码。
清单 4. 生成表达式树
/**
* 构造表达式树。首先通过词法分析构造表达式栈,然后构造表达式树。
* @param expr 输入表达式
* @return 表达式树
*/
public TreeNode buildTree(String expr) {
Stack<String> postExprStack = buildPostExpressionStack(expr);
Stack<String> tmpStack = reverseStack(postExprStack);
Stack<TreeNode> nodeStack = new Stack<TreeNode>();
while(!tmpStack.isEmpty()) {
String token = tmpStack.pop();
TreeNode node = new TreeNode(token);
TokenType nodeType = TableManager.getTokenType(token);
node.setNodeType(nodeType);
if(nodeType == TokenType.FUNCTION
|| nodeType == TokenType.OPERATOR
|| nodeType == TokenType.VARIABLE) {
int dimension = TableManager.getDimension(token);
TreeNode[] children = new TreeNode[dimension];
for(int j = dimension-1; j >= 0; j--){
children[j] = nodeStack.pop();
}
node.setChildren(children);
nodeStack.push(node);
} else {
nodeStack.push(node);
}
}
TreeNode root = nodeStack.pop();
return root;
}
|
分析与计算:该过程结合表管理器,通过递归分析与计算表达式树,得到表达式计算结果。
清单 5. 表达式分析与计算
/**
* 计算表达式。 通过递归解析计算表达式树得到计算结果。
* @param expr 输入表达式
* @return 计算结果
*/
public Variable computeExpression(String expr) {
Variable value = null;
if(expr == null) {
return value;
}
// 构造表达式树
TreeNode tree = buildTree(expr);
if(tree == null) {
return value;
}
// 解析计算表达式树
value = computeSubTree(tree);
return value;
}
/**
* 解析计算表达式子树
* @param node 子树根节点
* @return 子树计算结果
*/
public Variable computeSubTree(TreeNode node) {
Variable varRet = null;
if(node == null){
return null;
}
String value = node.getValue();
if(!TableManager.existOperator(value)
&& !TableManager.existFunc(value)
&& !TableManager.isValueOperator(value)){
return ParserUtil.getValue(value);
}
TreeNode[] children = node.getChildren();
if(children == null || children.length == 0) {
return ParserUtil.getValue(value);
}
Variable[] operands = new Variable[children.length];
for(int i = 0; i < children.length; i++) {
operands[i] = computeSubTree(children[i]);
}
OperationSymbol op = getOperationSymbol(node, value);
if(op != null) {
op.setOperands(operands);
varRet = op.operate();
}
return varRet;
}
|
表达式校验器:在表达式分析与计算的每一个过程中,都需要利用表达式校验器来保证其数据的合法性,如操作符是否合法、语法是否正确、分析得到的操作数数据类型是否正确、函数的参数类型是否正确等等。每当遇到校验失败的情况,都会抛出各种类型的异常,并中止解析过程,表示解析失败。
下面给出一个表达式解析引擎应用示例,如 清单 6 所示。
清单 6. 表达式解析引擎应用
public class ExpressionParserTester {
/*
* 初始化:注册用户自定义的函数以及变量到表达式解析引擎
*/
public static void init() {
TableManager.regFunction(
new Function("test",
"com.gavin.parser.expression.test.Test",
new DataType[]{DataType.INT,DataType.INT,DataType.INT},
DataType.INT,
true));
TableManager.regFunction(
new Function("test2",
"com.gavin.parser.expression.test.Test",
new DataType[]{DataType.STRING},
DataType.INT,
true));
TableManager.regVariable(new Variable(DataType.INT, "GB_VAR", 31));
}
public static void main(String[] args) {
init();
String expr =
"1+2*test($GB_VAR,test((1+3)+4*(5+6 ),2,(2+3)%2),
test(-10,10,11*(1+test(3,4,5))))+test2('300')*3";
TExprParser parser = TExprParser.getInstance();
// 测试 1: 建立后缀表达并打印
String postExp = parser.buildPostExpression(expr);
System.out.println(postExp);
// 测试 2: 解析以及计算表达式并打印结果
String value = parser.parse(expr);
System.out.println(value);
}
public static int test(int a, int b, int c) {
return a+b+c;
}
public static int test2(String param) {
return Integer.valueOf(param).intValue();
}
}
|
回页首
总结
本文以一种循序渐进的方式阐述了一种表达式解析与计算方法,并提供了一个支持可扩展的表达式解析与计算的设计实例。首先本文提出定义了表达式的一般模型及相关概念;然后从引入编译原理一般过程开始,逐步介绍了表达式的三种类型及表达式树的概念。最后提供一个设计实例来介绍表达式解析与计算的方法与步骤。笔者希望籍以本文为读者抛砖引玉,在表达式解析方面能提供些许指引。