Codeforces Gym 100379I Move the queen to the corner! 威佐夫博弈变形 + 高精度
题目大意:
就是现在有一个皇后在棋盘的左上角, 棋盘大小n*m, n , m<= 1e12 (就是被这个大范围卡了精度....)
然后两个人轮流移动皇后, 每次可以向下, 右或者右下斜线方向移动, 移动步数至少一步, 至多不超出棋盘边界..然后谁将这个皇后移动到了右下角谁就输了
大致思路:
首先如果是到右下角赢的话就是威佐夫博奕的原形了
这个地方谁到右下角谁输, 我们不妨记右下角是(0, 0)
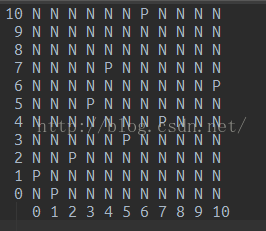
于是起点是(m - 1, n - 1), 我们画出P点和N点的示意图(必胜必败点示意图)如下:
可以你除了(1, 0), (0, 1), (2, 2)这3个P点的位置不同于威佐夫博弈之外, 其他的P点都是满足威佐夫博弈的性质的
那么对于这3个P点位置以及这3个位置能到达的点都特判一下, 然后对于其他的位置就是和威佐夫博弈一样的了
但是这题我用黄金分割比例的那个结论的时候, 写C++一直精度不够, long double也不行...于是最后换了Java重新写了一遍才过...
当然也有人不是用这个方法做的, 和斐波那契数列有关的方法...蒟蒻表示看不懂....
Java和C++的代码都附在下面了, 两者的逻辑是一样的...
不懂威佐夫博奕的可以看这里, 以及这里
代码如下:
Result : Accepted Memory : 0 KB Time : 560 ms
/*
* Author Gatevin
* Created Time : 2015/8/4 15:00:05
* File Name: Main.java
*/
import java.util.Scanner;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.util.Map;
import java.util.HashMap;
import java.util.Queue;
import java.util.LinkedList;
import java.io.FileOutputStream;
import java.math.BigDecimal;
public class Main{
public static String getGoldNumber(int n){
BigDecimal a = new BigDecimal(0.618);
BigDecimal b = new BigDecimal("1");
for (int i = 1; i < n+1; i++) {
a = b.divide(a.add(b), n, BigDecimal.ROUND_HALF_UP);
}
return a.toString();
}
public static boolean check(long x, long y)
{
if(x > y)
{
Long t = x; x = y; y = t;
}
if(x == 0 && y == 1) return true;
if(x == 0 && y != 1) return false;
if(x == 2 && y == 2) return true;
if(x == 2 && y != 2) return false;
if(x == 1) return false;
BigDecimal X = new BigDecimal(x);
long k = gold2.multiply(X).longValue();
BigDecimal K = new BigDecimal(k);
if(gold.multiply(K.add(one)).longValue() == x) k++;
K = new BigDecimal(k);
long tx = gold.multiply(K).longValue();
if(tx == x && y == x + k)
return true;
return false;
}
static String goldString = getGoldNumber(200);//精确到200位
static BigDecimal gold2 = new BigDecimal(goldString);
static BigDecimal one = new BigDecimal(1);
static BigDecimal gold = gold2.add(one);
public static void main(String args[]){
/*
//267914296 433494437
BigDecimal n = new BigDecimal(267914295);
BigDecimal m = new BigDecimal(433494436);
m = m.subtract(n);
m = m.multiply(g);
System.out.println(m);
*/
int T;
Scanner cin = new Scanner(System.in);
T = cin.nextInt();
long n, m;
for(int cas = 1; cas <= T; cas++)
{
n = cin.nextLong();
m = cin.nextLong();
long x = m - 1;
long y = n - 1;
if(check(x, y))
{
System.out.println(2);
continue;
}
if(x <= 2 || y <= 2)
{
if(x == 1 && y == 1)
System.out.println("1 1 0");
else if(x == 1 && y == 2)
System.out.println("1 2 0");
else if(x == 2 && y == 1)
System.out.println("1 0 2");
else
{
if(x == 1)
System.out.printf("1 %d 0\n", y);
else if(y == 1)
System.out.printf("1 0 %d\n", x);
else if(x == 2)
System.out.printf("1 %d 0\n", y - 2);
else if(y == 2)
System.out.printf("1 0 %d\n", x - 2);
}
continue;
}
if(x == y)
{
System.out.printf("1 %d %d\n",x - 2, y - 2);
continue;
}
if(Math.abs(x - y) == 1)
{
if(x > y)
System.out.printf("1 %d %d\n", y, y);
else
System.out.printf("1 %d %d\n", x, x);
continue;
}
if(Math.abs(x - y) >= 2)
{
BigDecimal xy = new BigDecimal(Math.abs(x - y));
long t = gold.multiply(xy).longValue();
if(x < y && t < x)
{
System.out.printf("1 %d %d\n", x - t, x - t);
continue;
}
if(y < x && t < y)
{
System.out.printf("1 %d %d\n", y - t, y - t);
continue;
}
}
BigDecimal X = new BigDecimal(x);
BigDecimal Y = new BigDecimal(y);
long k = gold2.multiply(X).longValue();
BigDecimal K = new BigDecimal(k);
if(gold.multiply(K.add(one)).longValue() == x) k++;
K = new BigDecimal(k);
long tx = gold.multiply(K).longValue();
if(k >= 2 && tx == x)
if(y > x + k)
{
System.out.printf("1 %d 0\n", y - (x + k));
continue;
}
k = gold2.multiply(gold2.multiply(X)).longValue();
K = new BigDecimal(k);
if(gold.multiply(gold.multiply(K.add(one))).longValue() == x) k++;
K = new BigDecimal(k);
tx = gold.multiply(gold.multiply(K)).longValue();
if(k >= 2 && tx == x)
if(y > x - k)
{
System.out.printf("1 %d 0\n", y - (x - k));
continue;
}
k = gold2.multiply(Y).longValue();
K = new BigDecimal(k);
if(gold.multiply(K.add(one)).longValue() == y) k++;
K = new BigDecimal(k);
long ty = gold.multiply(K).longValue();
if(k >= 2 && ty == y)
if(x > y + k)
{
System.out.printf("1 0 %d\n", x - (y + k));
continue;
}
k = gold2.multiply(gold2.multiply(Y)).longValue();
K = new BigDecimal(k);
if(gold.multiply(gold.multiply(K.add(one))).longValue() == y) k++;
K = new BigDecimal(k);
ty = gold.multiply(gold.multiply(K)).longValue();
if(k >= 2 && ty == y)
if(x > y - k)
{
System.out.printf("1 0 %d\n", x - (y - k));
continue;
}
System.out.println("What the fuck!");
}
}
}
另外还是发一下C++的版本吧....不过精度问题一直WA 11
Result : Wrong Answer on test 11
/*
* Author: Gatevin
* Created Time: 2015/8/14 15:12:26
* File Name: Sakura_Chiyo.cpp
*/
#include<iostream>
#include<sstream>
#include<fstream>
#include<vector>
#include<list>
#include<deque>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<cctype>
#include<cmath>
#include<ctime>
#include<iomanip>
using namespace std;
const double eps(1e-8);
typedef long long lint;
const double gold = (1 + sqrt(5.)) / 2;
const double gold2 = (sqrt(5.) - 1) / 2;
bool check(lint x, lint y)
{
if(x > y) swap(x, y);
if(x == 0 && y == 1) return 1;
if(x == 0 && y != 1) return 0;
if(x == 2 && y == 2) return 1;
if(x == 2 && y != 2) return 0;
if(x == 1) return 0;
lint k = floor(x*gold2);
if((lint)floor((k + 1)*gold) == x)
k++;
if((lint)floor(k*gold) == x && y == x + k)
return 1;
return 0;
}
int main()
{
int T;
//double xx = 1000000000001.999;
//printf("%I64d\n",(long long)floor(xx));
//printf("%I64d\n", (long long)xx);
//freopen("A.cpp", "r", stdin);
//freopen("out.out", "w", stdout);
scanf("%d", &T);
lint n, m;
while(T--)
{
scanf("%I64d %I64d", &n, &m);
lint x = m - 1, y = n - 1;//find a, b, such that (px - b, py - a) is P position
if(check(x, y))//P ?
{
puts("2");
continue;
}
//printf("1");
//x, y, <= 2 tepan
if(x <= 2 || y <= 2)
{
if(x == 1 && y == 1)
printf("1 1 0\n");
else if(x == 1 && y == 2)
printf("1 2 0\n");
else if(x == 2 && y == 1)
printf("1 0 2\n");
else
{
if(x == 1)
printf("1 %I64d 0\n", y);
else if(y == 1)
printf("1 0 %I64d\n", x);
else if(x == 2)
printf("1 %I64d 0\n", y - 2);
else if(y == 2)
printf("1 0 %I64d\n", x - 2);
}
continue;
}
if(x == y)
{
printf("1 %I64d %I64d\n", x - 2, y - 2);
continue;
}
if(abs(x - y) == 1)//go to 1, 0 or 0, 1
{
if(x > y)//1 0
{
printf("1 %I64d %I64d\n", y, y);
}
else//0 1
printf("1 %I64d %I64d\n", x, x);
continue;
}
//only remain go to gold point
if(abs(x - y) >= 2)//take 2 piles
{
lint t = (lint)floor(abs(x - y)*gold);
//cout<<"hehe"<<" "<<t<<" "<<abs(x - y)<<" "<<x<<" "<<y<<endl;
if(x < y)
{
if(t < x)
{
printf("1 %I64d %I64d\n", x - t, x - t);
continue;
}
}
if(y < x)
{
if(t < y)
{
printf("1 %I64d %I64d\n", y - t, y - t);
continue;
}
}
}
//else take one pile
//take y pile
//then x = A[i] or x = B[i]
//cout<<"now"<<endl;
//x = A[i]
lint k = floor(x*gold2);
if((lint)floor((k + 1)*gold) == x)
k++;
if(k >= 2 && (lint)floor(k*gold) == x)
if(y > x + k)
{
printf("1 %I64d 0\n", y - (x + k));
continue;
}
//x = B[i]
k = floor(x*gold2*gold2);
if((lint)floor((k + 1)*gold*gold) == x) k++;
if(k >= 2 && (lint)floor(k*gold*gold) == x)
{
if(y > x - k)
{
printf("1 %I64d 0\n", y - (x - k));
continue;
}
}
//cout<<"hehe"<<endl;
//take x pile
//y = A[i];
//cout<<"hehehe"<<endl;
k = floor(y*gold2);
if((lint)floor((k + 1)*gold) == y)
k++;
if(k >= 2 && (lint)floor(k*gold) == y)
if(x > y + k)
{
//cout<<0<<" "<<y + k<<" "<<x<<endl;
printf("1 0 %I64d\n", x - (y + k));
continue;
}
//y = B[i]
//cout<<"ppp"<<endl;
k = floor(y*gold2*gold2);
if((lint)floor((k + 1)*gold*gold) == y) k++;
if(k >= 2 && (lint)floor(k*gold*gold) == y)
{
if(x > y - k)
{
printf("1 0 %I64d\n", x - (y - k));
continue;
}
}
//cout<<"nani"<<endl;
//puts("2");
// printf("What the fuck %I64d %I64d\n", n, m);
// while( 1 );
}
return 0;
}