图算法 无圈图和关键路径分析
无圈图
如果已知图是无圈的,则可以利用拓扑顺序选择顶点来改进Dijkstra算法。由于选择和更新可以在拓扑排序执行的时候进行,因此算法能够一趟完成。
因为当一个顶点v被选取之后,按照拓扑排序法则它没有从unknown顶点发出的进入边,因此它的距离dv可不再被更新。这样的话,就不需要优先队列了。运行时间为O(|E| + |V|)。
关键路径分析
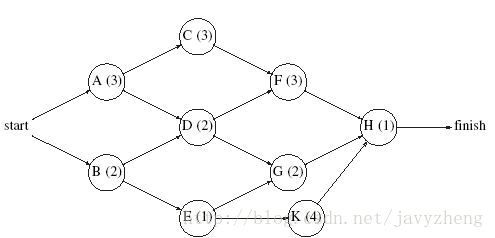
如图,每个节点表示一个必须执行的动作以及完成动作所花费的时间。该图叫做动作节点图。图中的边代表优先关系,一条边(v,w)意味着动作v必须在动作w开始前完成。(这意味着这个图必然是无圈的)。
这个图可以模拟两类问题:
1. 整个方案最早什么时间完成?
2. 确定哪些动作时可以延迟的,延迟多长,而不致影响最少完成时间?
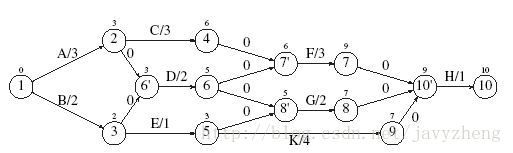
我们把动作节点图转化为事件节点图
1. 每个事件对应一个动作和所有相关的动作的完成;
2. 从事件节点图中的节点v可达到的事件可以在事件v完成后开始;
3. 在一个动作依赖于几个其他动作的情况下,可能需要插入哑边和哑节点(保证每个真实点只有一条入边)。
为了找出方案的最早完成时间,我们只要找出从第一个事件到最后一个事件的最长路径长度。
由于这是个无圈图,可以采纳最短路径算法计算图中所有节点的最早完成时间。
如果ECi是节点i的最早完成时间,则有
1. EC1 = 0;
2. ECw = max(ECv + c(v,w))
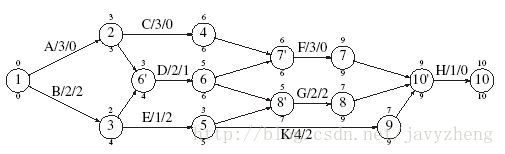
用以下法则计算每个节点最晚完成时间
1. LCn = ECn;//最后一个点的最晚完成时间和最早完成时间相同
2.LCv = min(LCw - c(v,w))
对于每个顶点,通过保存一个所有邻接且在先的顶点的表,这些值就可以以线性时间算出。借助顶点的拓扑顺序计算它们的最早完成时间,而最晚完成时间则通过倒转它们的拓扑顺序来计算。
每条边的松弛时间代表对应动作可以被延迟而又不至于推迟整体的完成的时间量。
Slack(v,w)= LCw - ECv - c(v,w)