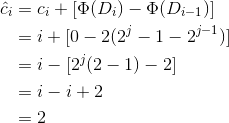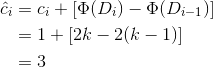《算法导论》笔记 第17章 17.3 势能方法
【笔记】
势能方法:已预付的工作表示成一种势能或势,他在需要时可以释放出来,以支付后面的操作。
势函数Φ将每个数据结构Di映射为一个实数Φ(Di),即与数据结构Di相联系的势。第i个操作的平摊代价c'i=ci+Φ(D_i)-Φ(D_{i-1})
n个操作总的平摊代价为∑c'i=∑ci+Φ(Dn)-Φ(D0)
如果定义一个势函数使得Φ(Dn)>=Φ(D0),则总的平摊代价∑c'i就是总的实际代价∑ci的一个上界。
通常定义Φ(D0)为0,证明对所有的i,有Φ(Di)>=0。
【练习】
17.3-1 假设有势函数Φ,使得对所有的i都有Φ(Di)>=Φ(D0),但是Φ(D0)≠0。证明:存在一个势函数Φ'使得Φ'(D0)=0,Φ'(Di)>=0,对所有i>=1,且用Φ'表示的平摊代价与用Φ表示的平摊代价相同。
令Φ'(Di)=Φ(Di)-Φ(D0)即可。
17.3-2 用势能方法的分析重做练习17.1-3。
设i=2^j+k,定义第i个操作Di的势函数Φ(Di)=2*k。
当k=0时,实际代价为i。
当k!=0时,实际代价为1。
所以第i个操作平摊代价为O(1)。
17.3-3 考虑一个包含n个元素的普通二叉最小堆数据结构,它支持最坏情况时间代价为O(lgn)的操作INSERT和EXTRACT-MIN。请给出一个势函数Φ,使得INSERT的平摊代价为O(lgn),EXTRACT-MIN的平摊代价为O(1),并证明函数确实是有用的。
17.3-4 假设某个栈在执行n个栈操作PUSH、POP和MULTIPOP之前包含s0个对象,结束后包含sn个对象,则这n个栈操作的总代价是多少?
17.3-5 假设一个计数器的二进制表示中在开始时有b个1,而不是0。证明:如果n=Ω(b),则执行n次INCREMENT操作的代价为O(n)。
17.3-6 说明如何用两个普通的栈来实现一个队列,使得每个ENQUEUE和DEQUEUE操作的平摊代价都为O(1)。
17.3-7 设计一个数据结构来支持整数动态多重集合S上的下列两个操作:
INSERT(S,x) 将x插入S中。
DELETE-LARGER-HALF(S)删除S中最大的floor(|S|/2)个元素。
解释如何实现这个数据结构,使得任意m个操作的序列在O(m)时间内运行,而且要在O(|S|)时间内输出S的元素。