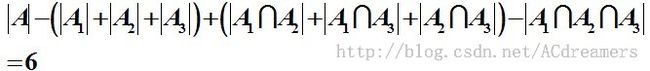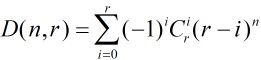容斥原理与多重集合
容斥原理与多重集合
首先介绍一个重要定理：
设S是有k种类型对象的多重集合，每种元素均具有无限的重复数。那么S的r组合的个数等于：
问题一：多重集合的组合问题
问题描述：给定3个a，4个b，5个c，现在要选10个元素，求一共有多少种组合？
分析：本问题就是相当于求S={3·a,4·b,5·c}的10组合数。
首先，多重集合的组合有一个定理，定理描述如下：
设S是有k种类型对象的多重集合，每种元素均具有无限的重复数，那么S的r组合的个数等于：
那么既然这样，我们令S∞={∞·a, ∞·b,∞·c}，那么S的10-组合数为
设集合A是S∞的10-组合全体，则|A|＝66，现在要求在10-组合中的a的个数小于等于3，b的个数小于等于4，c的个数小于等
于5的组合数.
定义性质集合P={P1,P2,P3},其中：
P1：10组合中a的个数大于等于4；
P2：10组合中b的个数大于等于5；
P3：10组合中c的个数大于等于6；
将满足性质Pi的10-组合全体记为Ai(1≤i≤3).
那么，A1中的元素可以看作是由S∞的10－4＝6组合再拼上4个a构成的，所以
同理有：
，
，
所以根据容斥原理，原问题的解为：
问题二：方程解的个数问题
(1)问题描述：已知非负整数
不大于7，求方程
整数解的个数。
分析：其实用容斥，跟上题一样，先求出总数，因为不可能出现两个或两个以上的数大于等于8，所以这里就简单很多了。
首先，S的10-组合数为：
，由于只会出现
中的一个大于等于8的情况，所以四种情况一样的，
其结果都是
，所以问题的解就是286-4*10=246
(2)问题描述：求方程
整数解的个数，其中
分析：对于这个问题需要先转化一下就跟上题一样了。
令：
，然后就有
，此类问题不再赘述。答案为21
问题三：集合划分问题
问题描述：将一个n元集合划分为r个非空子集，并给每个子集标上号1，2，3，...r，求划分方案数。
分析：设S为将n元集划分成有序r部分的全部划分方案集，注意这里每一部分可以为空，那么我们用总数减去为空的情况就可
以了，那么进一步有一个不为空，两个不为空，三个不为空，...等等。这样我们就可以容斥。
我们知道
，
， 
所以最后得到方案数为：