java排序算法(三):快排
要点
快速排序是一种
交换排序。
快速排序由C. A. R. Hoare在1962年提出。
它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分:分割点左边都是比它小的数,右边都是比它大的数。
然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
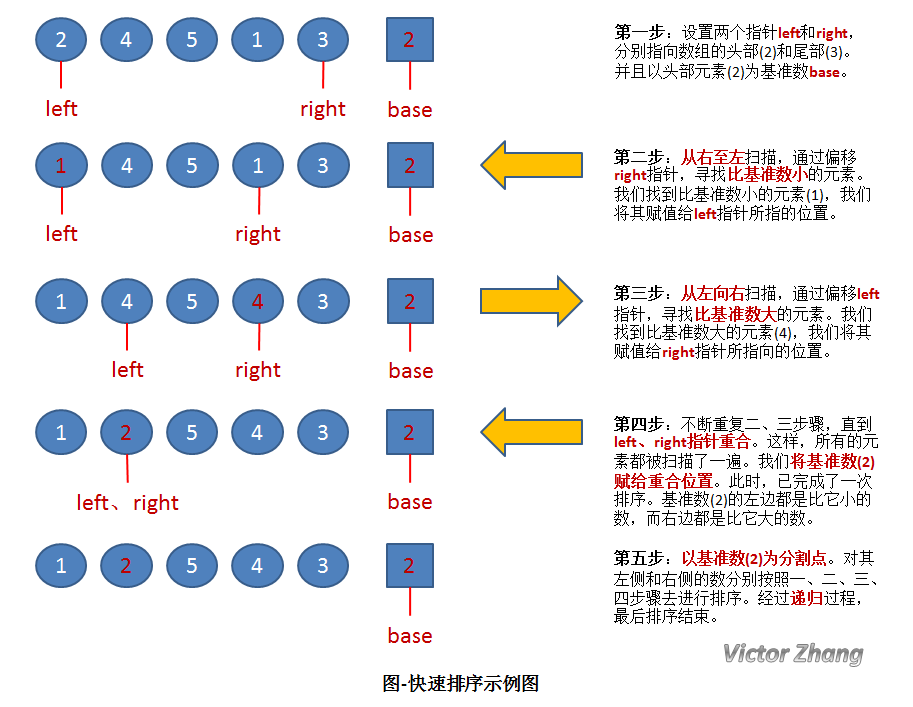
详细的图解往往比大堆的文字更有说明力,所以直接上图:
图-快速排序示例图中,演示了快速排序的处理过程:
初始状态为一组无序的数组:2、4、5、1、3。
经过以上操作步骤后,完成了第一次的排序,得到新的数组:1、2、5、4、3。
新的数组中,以2为分割点,左边都是比2小的数,右边都是比2大的数。
因为2已经在数组中找到了合适的位置,所以不用再动。
2左边的数组只有一个元素1,所以显然不用再排序,位置也被确定。(注:这种情况时,left指针和right指针显然是重合的。因此在代码中,我们可以通过设置判定条件left必须小于right,如果不满足,则不用排序了)。
而对于2右边的数组5、4、3,设置left指向5,right指向3,开始继续重复图中的一、二、三、四步骤,对新的数组进行排序。
import java.util.List;
public class quickSort {
public static void main(String[] args) {
int[] data={2,4,5,1,3,444,222,452532352};
quickSort quickSort = new quickSort();
quickSort.quickSort(data, 0, data.length-1);
for(int a: data){
System.out.print(a+" ");
}
}
public int divsion(int[] data,int left,int right){
//以最左边的数(left)为基准
int base = data[left];
while (left <right) {//左边的要小于右边
// 从序列右端开始,向左遍历,直到找到小于base的数
while(left<right && data[right]>=base ){
right--;
}
//从右往左找到了比base小的元素,将这个元素放到最左边left的位置
data[left]=data[right];
// 从序列左端开始,向右遍历,直到找到大于base的数
while (left<right && data[left]<=base) {
left++;
}
//从左往右 找到了比base大的元素,将这个元素放到最右边right的位置
data[right]=data[left];
}
// 最后将base放到left位置。此时,left位置的左侧数值应该都比left小
// 而left位置的右侧数值应该都比left大
data[left] = base;
//最后的是left=right,所以返回left和right都一样,都是中间的
//middle左边都是已经
int middle = left;
return left;
}
public void quickSort(int[] data ,int left ,int right){
// 左下标一定小于右下标,否则就越界了
if(left < right){
//对数组进行分割,取出下次分割的基准标号
int middle = divsion(data, left, right);
//对“基准标号“左侧的一组数值进行递归的切割,以至于将这些数值完整的排序
quickSort(data, left, middle-1);
//对“基准标号“右侧的一组数值进行递归的切割,以至于将这些数值完整的排序
quickSort(data, middle+1, right);
}
}
}