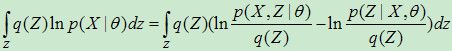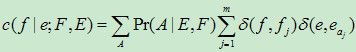EM算法

很碰巧，时隔一年了。面对经典的EM算法，我有了新的认识。经常有人谈到它就是"鸡生蛋，蛋生鸡"的解法，这个很通俗，但是只了解到这一层，是远不够的……

EM算法的全名是Expectation Maximization，中文名叫期望最大化算法。它是一个在含有隐变量的模型中常用的算法，在最大似然估计（MLE）和最大后验估计（MAP）中常用。在GMM、HMM、PCFG、IBM 5个对齐模型以及K-Means聚类方法中均有它的影子。下面会以MLE估计来介绍它，随后给出其两种证明方法，最后以实际模型中的应用为例，以期达到融会贯通的目的。

1. EM因什么而存在？

定义：观测变量X，针对X所获得的n个观测样本为() (数学上为了计算方便，一般认为它们之间满足独立同分布(independent and identically distributed, i.i.d)分布)，随机变量Z，是与观测变量对应的隐含变量，在所取n个样本中对应的取值为() (同样认为它们满足i.i.d分布)。参数变量为模型的一系列参数(注意，k的大小与n的大小没有关系)。因为我们在MLE估计中来讨论EM算法，所以这里，不是随机变量，而是普通的变量。

依照最大似然估计(Maximum Likelihood Estimation, MLE)，形式化定义为：

 (1)

在某些问题中由于存在隐含的随机变量Z，故由边缘分布的概念知道有：

 (2)

(2)式在很多时候是intractable(可以回顾HMM和PCFG中的情形)。这时需要另辟蹊径，而EM正是解决这类问题的有力武器。

1.1问题诠释

*** 为什么会有隐含变量？

存在隐含变量，是EM不同于一般的MLE问题的本质。隐含变量，可能是模型中真正存在的(如HMM，PCFG中的参数求解)，也可能是为了求解方便而引入的。

2. EM收敛到最大似然的2种证明

以最大似然为目标函数，EM能收敛吗？下面我们将给出两种证明。第一种证明是通过不断提高下界的思路来证，更能表达EM的本质；而第二种证明却是我们常在实际中应用EM的思路。

2.1 优化下界的证法

先做一些基础的推导：

(1) 拆分：

(2) 等式两边同乘以q(Z)，并对Z求和：

(3) 由于Z与独立，且，于是，

(4) 引入两个函数：

这时，可以简化为：

注意，，等号在p=q时成立。所以是的下界。而EM算法的思路就是靠不断的提高下界，来找到的最大值。再回顾一下，直接计算有时候是件困难/复杂的事情。不过计算是比较容易的。那么如何提高下界呢？EM算法的E步和M步正是来实现这个目标的。

E步：假设当前的参数为，固定，找一个分布q(Z)，使得最大。但是注意到与Z无关，所以使最大，等价于使最小(=0)，也就是说。

M步：固定q(Z)，找新参数，使得最大。当然，的增大可能来自于两部分：和，毕竟此时和一般是不同的，所以。

2.2 常规思路的证法

同样我们先做一些基础的推导：

回到，我们知道

那么等式两边去对数，得到

等式两边都加上对关于Z的条件概率分布的积分，我们得到：

（注意：对比前一个证法，这里是与那有相似之处的。那里是引入了q(Z)，而这里是直接将，同时这边少了可以消掉的lnq(Z)项）

引入两个函数来分别表示上式右边的两项：

 (4)

 (5)

这样，就可以表示为：

 (6)

（注意：(4)(5)(6)式都是关于的函数）

好，如果对，在迭代求解中有，那么就有理由说EM收敛是可能的。那如何从构造，才能使得成立？

 

接下来，我们寻找一种办法来构造：

对，应用(6)有：

在这，我们首先尝试去证明，然后尝试去最大化。

首先证明。

是关于的函数，且在处取得函数的最大值，即当时，。

而实际上

(中间对上凸函数应用了Jensen不等式)

证毕。

所以只要我们保证成立，那么就能保证成立。当然这点很容易保证，即我们选择为使取最大值的，即。

 

======================================

以上面的思路就已经证明了可以选出一个，它使得，也就是我们已经找到一个迭代求解的方法（这种方法就叫EM）使得收敛。总结EM算法如下：

=================================

E步：计算关于的函数(其形式本质上是期望)

M步：

(循环做E步和M步)

=================================

总结来说，EM算法就是通过迭代地最大化完整数据的对数似然函数的期望，来最大化不完整数据的对数似然函数。

2.3 两种证法的等价性

关于两种证法在最大化目标的解释，第一种方法是在最大化

，当然在E步得出。

第二种方法是在最大化

。

其实两个是等价的，把代入得到：

注意到，第一种方法，M步是固定寻找，因此上式的后一项是常数。所以最大化，等价于在最大化上式的前一项，从形式上看，就是。所以两种证法是等价的。

3. EM应用场景

3.1 IBM Model

(1) 隐变量确实是对齐吗？

答：是的，确实是词与词之间的对齐。

(2) EM是算似然概率的(指，)，那么在IBM模型中哪里体现了似然概率？

答：分别在P(F|E), P(F,A|E)中。参数是融于公式中的词汇翻译概率、位置扭曲概率以及繁殖概率等等。

(3) E步在算谁？

答：以Model 1为例，E步算的就是：

形式上仍是log-likelihood在关于隐藏变量的某种概率分布下的期望。

(对比)

3.2 GMM、HMM、PCFG

对于它们以及词语对齐模型，隐变量都是辅助描述模型的某种"结构"，如对于HMM，隐变量是状态转移序列这种结构，参数是状态转移概率和发射概率；对于GMM，隐变量是样本点所属的类别这种结构，参数是这些高斯分布的相关参数；对于PCFG，隐变量是指句法分析树这种结构，参数是规则概率。

4. EM变种

4.1 Variational EM

有些时候，是不能显式的计算出来，这个时候最大化就显得相当困难。这个时候，可以考虑不一定保证Jensen不等式一定要取等号，如果给定某种形式，就得到variational EM算法。

4.2 EM for MAP

上面讲的是针对MLE估计的EM算法，其实也有针对MAP估计的EM算法。

4.2 Online EM

上面讲的是EM可以归于batch EM一类，还有文献介绍关于online EM的论述。可以在文献[2]中阅读到有关online EM的内容。

5. 总结

EM算法就是通过迭代地最大化完整数据的对数似然函数的期望，来最大化不完整数据的对数似然函数。当然，针对各种EM的变形，它们又有各自的应用场景。