【Good Bye 2014C】【脑洞】New Year Book Reading 书放一摞依次看 最佳顺序使费用最小
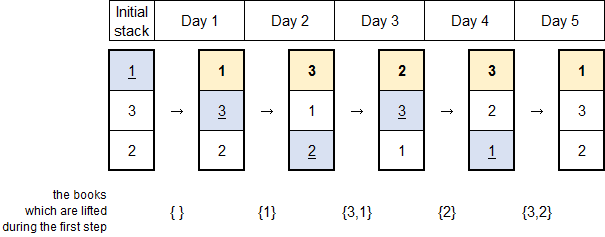
New Year is coming, and Jaehyun decided to read many books during 2015, unlike this year. He has n books numbered by integers from 1 to n. The weight of the i-th (1 ≤ i ≤ n) book is wi.
As Jaehyun's house is not large enough to have a bookshelf, he keeps the n books by stacking them vertically. When he wants to read a certain book x, he follows the steps described below.
- He lifts all the books above book x.
- He pushes book x out of the stack.
- He puts down the lifted books without changing their order.
- After reading book x, he puts book x on the top of the stack.
He decided to read books for m days. In the j-th (1 ≤ j ≤ m) day, he will read the book that is numbered with integer bj (1 ≤ bj ≤ n). To read the book, he has to use the process described in the paragraph above. It is possible that he decides to re-read the same book several times.
After making this plan, he realized that the total weight of books he should lift during m days would be too heavy. So, he decided to change the order of the stacked books before the New Year comes, and minimize the total weight. You may assume that books can be stacked in any possible order. Note that book that he is going to read on certain step isn't considered as lifted on that step. Can you help him?
The first line contains two space-separated integers n (2 ≤ n ≤ 500) and m (1 ≤ m ≤ 1000) — the number of books, and the number of days for which Jaehyun would read books.
The second line contains n space-separated integers w1, w2, ..., wn (1 ≤ wi ≤ 100) — the weight of each book.
The third line contains m space separated integers b1, b2, ..., bm (1 ≤ bj ≤ n) — the order of books that he would read. Note that he can read the same book more than once.
Print the minimum total weight of books he should lift, which can be achieved by rearranging the order of stacked books.
3 5 1 2 3 1 3 2 3 1
12
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<string>
#include<ctype.h>
#include<math.h>
#include<set>
#include<map>
#include<vector>
#include<queue>
#include<bitset>
#include<algorithm>
#include<time.h>
using namespace std;
void fre() { freopen("c://test//input.in", "r", stdin); freopen("c://test//output.out", "w", stdout); }
#define MS(x,y) memset(x,y,sizeof(x))
#define MC(x,y) memcpy(x,y,sizeof(x))
#define MP(x,y) make_pair(x,y)
#define ls o<<1
#define rs o<<1|1
typedef long long LL;
typedef unsigned long long UL;
typedef unsigned int UI;
template <class T1, class T2>inline void gmax(T1 &a, T2 b) { if (b>a)a = b; }
template <class T1, class T2>inline void gmin(T1 &a, T2 b) { if (b<a)a = b; }
const int N = 505, M = 0, Z = 1e9 + 7, ms63 = 0x3f3f3f3f;
int n, m;
int w[N];
int b[N];
int main()
{
while (~scanf("%d%d", &n,&m))
{
for (int i = 1; i <= n; ++i)scanf("%d", &w[i]);
int bot = 0;
int ans = 0;
for (int i = 1; i <= m; ++i)
{
int r; scanf("%d", &r);
bool flag = 0;
for (int j = 1; j <= bot; ++j)
{
if (b[j] == r)
{
flag = 1;
for (int k = j; k >= 1; --k)b[k] = b[k - 1];
b[1] = r;
break;
}
ans += w[b[j]];
}
if (!flag)
{
++bot;
for (int k = bot; k >= 1; --k)b[k] = b[k - 1];
b[1] = r;
}
}
printf("%d\n", ans);
}
return 0;
}
/*
【trick&&吐槽】
最大的答案可能是n*m*100=5e7,int足以。
【题意】
有n(500)本书,成一摞。
我们有一个看书的顺序。
要看第i本书的时候,
我们要——
1,把这本书之上的书搬走,体力成本加上这本书之上的书的重量之和,再放回之上的所有书(不改变顺序);
2,看这本书,把这本书放在最上面。
问你初始的书从上到下的顺序可以是怎么样,能够使得我们的体力成本最小
【类型】
脑洞
【分析】
显然,我们书的初始摆放顺序就按照我们看书的顺序就好了。
否则,我们还要浪费多余成本的调整成这个样子。
于是按照这个原则贪心下去就可以得到最优解。
【时间复杂度&&优化】
O(nm)
*/