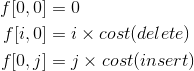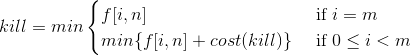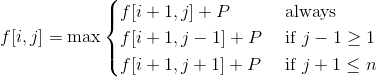《算法导论》笔记 第15章 总结与思考

【总结】

【思考】

15-1 双调欧几里得旅行商问题

POJ 2677 Tour

欧几里得旅行商问题是对平面上给定的n个点，确定一条连接各点的最短闭合旅程的问题。这个解的一般形式为NP完全的。

J.L. Bentley 建议通过只考虑双调旅程(bitonictour)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。

在这种情况下，多项式时间的算法是可能的。描述一个确定最优双调路线的O(n^2)时间的算法。

将点按照横坐标从小到大排序并编号为1,2...n。

令dist[i,j]表示点i与点j之间的距离。

定义f[i,j](i>j)为从点i向左到点1，从点1向右到点j的最短距离。

1、当j<i-1时，f[i,j]=f[i-1,j]+dist[i-1][i]。

2、当j=i-1时，f[i,j]=min(f[j][k]+dist[k][i])(k<j)。

double dp(int i,int j) {
    if (f[i][j] >= 0) return f[i][j];
    if (j < i-1) f[i][j] = dp(i-1,j) + dist[i][i-1];
    else {
        double res = OO;
        for (int k=1;k<i-1;k++) {
            res = min(res, dp(i-1,k) + dist[k][i]);
        }
        f[i][j] = res;
    }
    return f[i][j];
}
void getDist() {
    for (int i=1;i<=n;i++) {
        for (int j=1;j<i;j++) {
            dist[i][j] = dist[j][i] = sqrt( (a[i].x-a[j].x)*(a[i].x-a[j].x) + (a[i].y-a[j].y)*(a[i].y-a[j].y) );
        }
    }
}
double tour() {
    sort(a+1,a+1+n,cmp);
    getDist();
    for (int i=1;i<=n;i++) {
        for (int j=1;j<=n;j++) {
            f[i][j]=-OO;
        }
    }
    f[2][1] = dist[2][1];
    return dp(n,n-1)+dist[n][n-1];
}

15-2 整齐打印

考虑在一个打印机上整齐地打印一段文章的问题。输入的正文是n个长度分别为L1、L2、……、Ln（以字符个数度量）的单词构成的序列。我们希望将这个段落在一些行上整齐地打印出来，每行至多M个字符。“整齐度”的标准如下：如果某一行包含从i到j的单词（i<j），且单词之间只留一个空格，则在行末多余的空格字符个数为 M - (j-i) - (Li+ …… + Lj)，它必须是非负值才能让该行容纳这些单词。我们希望所有行（除最后一行）的行末多余空格字符个数的立方和最小。请给出一个动态规划的算法，来在打印机整齐地打印一段又n个单词的文章。分析所给算法的执行时间和空间需求。

令w[i,j]表示将单词i至单词j放入同一行的多余空格字符的立方和。

f[i]表示将前i个单词放入文章所能得到的最小立方和。注意w[j+1,i]<0时不进行计算。

15-3 编辑距离

初始化：

状态转移方程：

消灭：

15-4 计划一个公司聚会

f[i]表示在以i为根的子树中，选取结点i，所能获得的最大欢乐。

g[i]表示在以i为根的子树中，不选取结点i，所能获得的最大欢乐。

15-5 Viterbi算法

15-6 在棋盘上移动

15-7 达到最高效益的调度

按deadline排序后用01背包解。