UVA 11235 Frequent values (RMQ)
You are given a sequence of n integers a1 , a2 , ... , an in non-decreasing order. In addition to that, you are given several queries consisting of indices i and j (1 ≤ i ≤ j ≤ n). For each query, determine the most frequent value among the integers ai , ... , aj.
Input Specification
The input consists of several test cases. Each test case starts with a line containing two integers n and q (1 ≤ n, q ≤ 100000). The next line contains n integers a1 , ... , an(-100000 ≤ ai ≤ 100000, for each i ∈ {1, ..., n}) separated by spaces. You can assume that for each i ∈ {1, ..., n-1}: ai ≤ ai+1. The following q lines contain one query each, consisting of two integers i and j (1 ≤ i ≤ j ≤ n), which indicate the boundary indices for the query.
The last test case is followed by a line containing a single 0.
Output Specification
For each query, print one line with one integer: The number of occurrences of the most frequent value within the given range.
Sample Input
10 3
-1 -1 1 1 1 1 3 10 10 10
2 3
1 10
5 10
0
Sample Output
1
4
3
题意:
输入一个n个元素的非减序列a[],接着进行q次询问,每次询问输入两个数L, R, 问a[L]与a[R]之间相同元素的个数最多有多少个。
思路: 把每个相同的连续串合并到一起 分成多个段 段的数值一样 : 用(a,b)表示有b个连续的a ,用num[pos] ,left[pos],right[pos] 分别表示位置pos所在的段的编号 和左右端点位置 用value[i]表示第i段的数值,用count[i]表示第i段的出现次数
对于查询L, R ,如果L, R在同一段 则结果为R-L+1
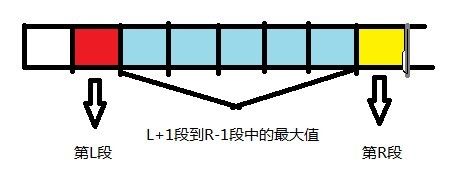
如果不在同一段 则为求这中间多个段内的最大的count[i]值(RMQ) 以及L, R所在的段的连续个数的最大值
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
using namespace std;
int mark[100005],num[100005];
int lefts[100005],rights[100005],maxsum[100005][25];
//用num[i]来记录第re段相等的元素有多少个,用一个mark数组记录下标为i的元素属于第几段
//left数组记录re段元素的上界,right数组记录re段元素的下界,这里的上界下界指的是下标
int re,value;//re表示第几段,value是用来判断每次输入的元素是不是跟前一个相等
void RMQ()
{
for(int i=1; i<=re; ++i)
maxsum[i][0]=num[i];
for(int j=1; (1<<j)<=re+1; ++j)
for(int i=1; i+(1<<j)-1<=re; ++i)
maxsum[i][j]=max(maxsum[i][j-1],maxsum[i+(1<<(j-1))][j-1]);
}
int Max(int a,int b,int c)
{
if(a<b) a=b;
if(a<c) a=c;
return a;
}
int main()
{
int n,q;
while(cin>>n&&n!=0)
{
int L,R,x;//这n个数我们都用x表示
memset(num,0,sizeof(num));
memset(mark,0,sizeof(mark));
memset(lefts,0,sizeof(lefts));
memset(rights,0,sizeof(rights));
memset(maxsum,0,sizeof(maxsum));
re=1; //re记录的是第几段
cin>>q;
cin>>x;
value=x;
num[1]=1;
mark[1]=1;
lefts[1]=1;
for(int i=2;i<=n; ++i)
{
scanf("%d",&x);
if(x==value)
{
num[re]++;
mark[i]=re;
}
else
{
rights[re]=i-1;
re++;
mark[i]=re;
num[re]=1;
lefts[re]=i;
value=x;
}
}
RMQ();
while(q--)
{
scanf("%d%d",&L,&R);
if(mark[L]==mark[R])
cout<<R-L+1<<endl;
else
{
int ans=0;
if(mark[L]+1<=mark[R]-1) //如果两段中存在段
{
int k=(int)((log(mark[R]-mark[L]-1))/log(2.0));
ans=max(maxsum[mark[L]+1][k],maxsum[mark[R]-(1<<k)][k]);
}
ans=Max(rights[mark[L]]-L+1,ans,R-lefts[mark[R]]+1);
cout<<ans<<endl;
}
}
}
return 0;
}