poj 3131 Cubic Eight-Puzzle (双向bfs+深度控制 立体八数码)
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 1344 | Accepted: 451 |
Description
Let’s play a puzzle using eight cubes placed on a 3 × 3 board leaving one empty square.
Faces of cubes are painted with three colors. As a puzzle step, you can roll one of the cubes to a adjacent empty square. Your goal is to make the specified color pattern visible from above by a number of such steps.
The rules of this puzzle are as follows.
-
Coloring of Cubes: All the cubes area colored in the same way as shown in Figure 1. The opposite faces have the same color.
Figure 1: Coloring of a cube
-
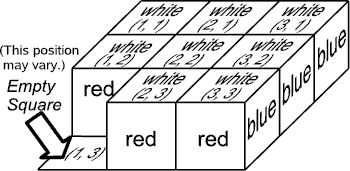
Initial Board State: Eight cubes are placed on the 3 × 3 board leaving one empty square. All the cubes have the same orientation as shown in Figure 2. As shown in the figure, squares on the board are given xand y coordinates, (1, 1), (1, 2), …, and (3, 3). The position of the initially empty square may vary.
Figure 2: Initial board state
-
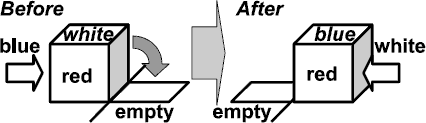
Rolling Cubes: At each step, we can choose one of the cubes adjacent to the empty square and roll it into the empty square, leaving the original position empty. Figure 3 shows an example.
Figure 3: Rolling a cube
-
Goal: The goal of this puzzle is to arrange the cubes so that their top faces form the specified color pattern by a number of cube rolling steps described above.
Your task is to write a program that finds the minimum number of steps required to make the specified color pattern from the given initial state.
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets is less than 16. Each dataset is formatted as follows.
x y F11 F21 F31 F12 F22 F32 F13 F23 F33
The first line contains two integers x and y separated by a space, indicating the position (x, y) of the initially empty square. The values of x and y are 1, 2, or 3.
The following three lines specify the color pattern to make. Each line contains three characters F1j, F2j, and F3j, separated by a space. Character Fij indicates the top color of the cube, if any, at the position (i, j) as follows:
B:Blue,
W:White,
R:Red,
E:the square is Empty.
There is exactly one ‘E’ character in each dataset.
Output
For each dataset, output the minimum number of steps to achieve the goal, when the goal can be reached within 30 steps. Otherwise, output “-1” for the dataset.
Sample Input
1 2 W W W E W W W W W 2 1 R B W R W W E W W 3 3 W B W B R E R B R 3 3 B W R B W R B E R 2 1 B B B B R B B R E 1 1 R R R W W W R R E 2 1 R R R B W B R R E 3 2 R R R W E W R R R 0 0
Sample Output
0 3 13 23 29
30 -1 -1
题意:这是一个立体的8数码问题,不过有点区别,有8个立体的正方体摆在3*3的区域内,留一个空格方便移动。移动的规则是:空格旁边的小正方体可以滚动到空格位置,小正方体原来的位置变成空格。每个小正方体6个面有3中颜色,对面颜色相同,分别是white,blue,red。初始状态每个小正方体的摆放方式都一样,从正面看上面是white,前面是red,右面是blue,空格位置给定。现在给定一个初始的空格位置以及一个终态的上表面的颜色分布,求是否能在30步内从初态到终态,能,输出最少步数,不能,输出-1,注意给定的终态只是上表面的颜色分布,其他面上的颜色不做要求。
思路:bfs。这题状态数非常之多,时间空间都要求很高,如果单向bfs,时空复杂度都太高,因此选择双向bfs。首先要解决的是判重问题,这题不像二维平面的8数码,每个位置只有一个状态,因此可以用康托判重,这题每个位置的小方块有6个状态,加上空格,每个位置有7个状态,那么总的状态数就是7^9,显然还是太大了。再考虑到9个位置只能有一个位置是空格,可以把空格单独拿出来判重,这样空间复杂度就降到了6^8*9,勉强可以接受。
这就需要用六进制数表示状态,然后判重也好判了,最后的问题就是模拟方块的滚动了,4个方向滚动,状态会发生怎样的变化都要在草稿纸上画清楚。
ps:这题还要说明一点 因为初状态只有一种 末状态却有2^8种 所以从前往后搜和从后往前搜搜的深度得不一样才行 从前往后多搜点 才能保证双搜沿棱形展开 我是这样控制的 从前往后:21层 从后往前:9层。
感想:这题程序代码还是蛮长的 所以要思路清晰 想好了 准备好了再下手 不然debug会很不好搞的
代码:(我的程序用的STL 也可以改为自己的队列的 会快一点点 方便看 我就只贴STL代码好了 )
// Memory 31352 KB Time 2250 ms#include <iostream> #include <cstdio> #include <cstring> #include <queue> #define maxn 1679616 // 6^8 using namespace std; int n,m,x,y,ans,dfspos; int six[]= {1,6,36,216,1296,7776,46656,279936}; int state[3][3]; // 根据前上推状态 int roll[6][4]= // 状态滚动后的状态 { 2,2,5,5, 4,4,3,3, 0,0,4,4, 5,5,1,1, 1,1,2,2, 3,3,0,0 }; bool vis1[9][maxn]; bool vis2[9][maxn]; int mp[9]; int dx[]= {-1,1,0,0}; int dy[]= {0,0,-1,1}; int undir[]= {1,0,3,2}; int dight[8]; struct Node { int pos; int sta; int step; } cur,now; queue<Node>q1,q2; int getdight(int xx,int k) // 开始是按十进制提取的 想错了 应该是提取六进制 { int i,j,t; if(k==0) t=xx%6; else { t=1; for(i=1; i<=k; i++) t*=6; t=(xx/t)%6; } return t; } bool bfs(int k) { int i,j,mi,cnt1,cnt2,npos,nsta,nx,ny,temp,nstep,flag; int tx,ty,tpos,tsta,tstadt; memset(vis1,0,sizeof(vis1)); while(!q1.empty()) q1.pop(); cur.pos=k; cur.sta=0; vis1[k][0]=1; cur.step=0; q1.push(cur); cnt1=0; cnt2=0; while(1) { flag=0; while(q1.front().step<=cnt1&&!q1.empty()) { flag=1; now=q1.front(); q1.pop(); npos=now.pos; nsta=now.sta; nstep=now.step; nx=npos/3; ny=npos%3; if(vis2[npos][nsta]) { ans=nstep+cnt2; return true ; } // printf("pos:%d step:%d sta:%d nx:%d ny:%d\n",npos,nstep,nsta,nx,ny); for(i=0; i<8; i++) { dight[i]=getdight(nsta,i); } for(i=0; i<4; i++) { tx=nx+dx[i]; ty=ny+dy[i]; if(tx>=0&&tx<3&&ty>=0&&ty<3&&nstep<21) { // printf("tx:%d ty:%d\n",tx,ty); tpos=tx*3+ty; if(i==2||i==3) // 左右滚动不会改变相对位置大小 可直接处理 { mi=npos>tpos?tpos:npos; tstadt=roll[dight[mi]][undir[i]]; tsta=nsta-six[mi]*dight[mi]+six[mi]*tstadt; if(!vis1[tpos][tsta]) { vis1[tpos][tsta]=1; cur.step=nstep+1; cur.pos=tpos; cur.sta=tsta; q1.push(cur); } } else if(i==0) // 向下滚动 要影响三个数的值 { tstadt=roll[dight[tpos]][undir[i]]; tsta=nsta; for(j=tpos; j<npos; j++) { tsta-=six[j]*dight[j]; } tsta+=tstadt*six[npos-1]; for(j=tpos+1; j<npos; j++) { tsta+=six[j-1]*dight[j]; } if(!vis1[tpos][tsta]) { vis1[tpos][tsta]=1; cur.step=nstep+1; cur.pos=tpos; cur.sta=tsta; q1.push(cur); } } else if(i==1) // 向上滚动 也要影响三个数的值 { tstadt=roll[dight[tpos-1]][undir[i]]; tsta=nsta; for(j=npos; j<tpos; j++) { tsta-=six[j]*dight[j]; } tsta+=tstadt*six[npos]; for(j=npos; j<tpos-1; j++) { tsta+=six[j+1]*dight[j]; // 开始就错在这里了 j忘记+1了 } if(!vis1[tpos][tsta]) { vis1[tpos][tsta]=1; cur.step=nstep+1; cur.pos=tpos; cur.sta=tsta; q1.push(cur); } } } } } if(cnt1<21) cnt1++; // 设置深度 从前往后不超过21层 while(q2.front().step<=cnt2&&!q2.empty()) { flag=1; now=q2.front(); q2.pop(); npos=now.pos; nsta=now.sta; nstep=now.step; nx=npos/3; ny=npos%3; if(vis1[npos][nsta]) { ans=cnt1+nstep; return true ; } // printf("pos:%d step:%d sta:%d nx:%d ny:%d\n",npos,nstep,nsta,nx,ny); for(i=0; i<8; i++) { dight[i]=getdight(nsta,i); } for(i=0; i<4; i++) { tx=nx+dx[i]; ty=ny+dy[i]; if(tx>=0&&tx<3&&ty>=0&&ty<3&&nstep<9) { // printf("tx:%d ty:%d\n",tx,ty); tpos=tx*3+ty; if(i==2||i==3) // 左右滚动不会改变相对位置大小 可直接处理 { mi=npos>tpos?tpos:npos; tstadt=roll[dight[mi]][undir[i]]; tsta=nsta-six[mi]*dight[mi]+six[mi]*tstadt; if(!vis2[tpos][tsta]) { vis2[tpos][tsta]=1; cur.step=nstep+1; cur.pos=tpos; cur.sta=tsta; q2.push(cur); } } else if(i==0) // 向下滚动 要影响三个数的值 { tstadt=roll[dight[tpos]][undir[i]]; tsta=nsta; for(j=tpos; j<npos; j++) { tsta-=six[j]*dight[j]; } tsta+=tstadt*six[npos-1]; for(j=tpos+1; j<npos; j++) { tsta+=six[j-1]*dight[j]; } if(!vis2[tpos][tsta]) { vis2[tpos][tsta]=1; cur.step=nstep+1; cur.pos=tpos; cur.sta=tsta; q2.push(cur); } } else if(i==1) // 向上滚动 也要影响三个数的值 { tstadt=roll[dight[tpos-1]][undir[i]]; tsta=nsta; for(j=npos; j<tpos; j++) { tsta-=six[j]*dight[j]; } tsta+=tstadt*six[npos]; for(j=npos; j<tpos-1; j++) { tsta+=six[j+1]*dight[j]; } if(!vis2[tpos][tsta]) { vis2[tpos][tsta]=1; cur.step=nstep+1; cur.pos=tpos; cur.sta=tsta; q2.push(cur); } } } } } if(cnt2<9) cnt2++; // 从后往前不超过9步 if(!flag) return false ; } } void dfs(int kk,int ssta,int tt) // 访问到第几个数 状态 已经加进来了几个数 { int i,j,temp; if(kk>8) { if(!vis2[dfspos][ssta]) // 这里的dfspos得用全局变量 { vis2[dfspos][ssta]=1; cur.step=0; cur.sta=ssta; // printf("pos:%d ssta:%d\n",dfspos,ssta); q2.push(cur); } return ; } if(mp[kk]==-1) { dfspos=kk; dfs(kk+1,ssta,tt); } else { temp=mp[kk]*six[tt]; dfs(kk+1,ssta+temp,tt+1); temp=(mp[kk]+1)*six[tt]; dfs(kk+1,ssta+temp,tt+1); } } int main() { int i,j,t,tst,tpos,temp; char s[3]; state[0][1]=0; state[0][2]=1; state[1][0]=2; state[1][2]=3; state[2][0]=4; state[2][1]=5; while(scanf("%d%d",&x,&y),x||y) { x--; y--; t=y*3+x; for(i=0; i<3; i++) { for(j=0; j<3; j++) { scanf("%s",s); temp=i*3+j; if(s[0]=='W') mp[temp]=0; else if(s[0]=='R') mp[temp]=2; else if(s[0]=='B') mp[temp]=4; else { mp[temp]=-1; tpos=i*3+j; } } } cur.pos=tpos; memset(vis2,0,sizeof(vis2)); while(!q2.empty()) q2.pop(); dfs(0,0,0); // 将终态进队列 if(bfs(t)) printf("%d\n",ans); else printf("-1\n"); } return 0; }