Manacher's ALGORITHM

文章转载于Felix's Blog,在此谢过，便于理解，文章有稍微改动。

Manacher's ALGORITHM: O(n)时间求字符串的最长回文子串

首先用一个非常巧妙的方式对子串预处理：

(1)将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度：在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。 

(2)为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#。

举例：

下面以字符串12212321为例，经过上一步，变成了 S[] = "$#1#2#2#1#2#3#2#1#";

然后用一个数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度（包括S[i]），比如S和P的对应关系：

S  #  1  #  2   #  2  #  1   #  2  #  3  #  2  #  1  #
P  1  2  1  2  5  2  1  4  1  2  1  6  1  2  1  2  1
(p.s. 可以看出， P[i]-1正好是原字符串中回文串的总长度）

那么怎么计算P[i]呢？该算法增加两个辅助变量（其实一个就够了，两个更清晰）id和mx，

其中id表示最大回文子串中心的位置，mx则为id+P[id]，也就是最大回文子串的边界。

------------

注意：在算法中,id和mx是一直更新的，其表示，以id为起点，半径为mx势力范围内能够罩住的区间,即[id - mx,id + mx]。

在处理第i个字符时，如果mx > i，则说明该字符在以id为起点的势力区间范围内，第i个字符能用的上一次处理的结果，可以不用去匹配而直接获得已经匹配的字符个数。需要注意的是，此时直接获得的已经匹配的字符个数不一定是最终匹配的个数。原因会在下面讨论。

如果不在势力范围内，只能按照普通的方法挨个匹配喽。

这里需要说明下，对于字符S[t],它的回文子串时以t开始，半径为mx。

则表示，S[t - mx] != S[t + mx],即以S[t]为中心的回文子串是不包含字符S[t + mx]的。

因为字符t的回文子串时以t开始，如果包含mx，则其回文子串区间为[t,t+mx],其长度应该为（t + mx） - mx + 1 = t + 1。(包含两个端点的区间长度等于两个端点差 + 1)。这与其半径为mx，是相反的。故不包含字符S[t + mx]。

下面给出一个结论。

------------

然后可以得到一个非常神奇的结论，这个算法的关键点就在这里了：

如果mx > i，那么P[i] >= MIN(P[2 * id - i], mx - i)，其中i与j关于id对称。

就是这个串卡了我非常久。实际上如果把它写得复杂一点，理解起来会简单很多：

//记j = 2 * id - i，也就是说 j 是 i 关于 id 的对称点。
if (mx - i > P[j]) 
    P[i] = P[j];
else /* P[j] >= mx - i */
    P[i] = mx - i; // P[i] >= mx - i，取最小值，之后再匹配更新。

当然光看代码还是不够清晰，还是借助图来理解比较容易。

第一种情况：

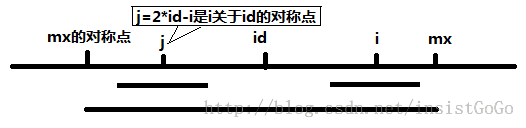
当 mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

------------------------------

说明：

在图中，给出两个条件：

（1）mx > i :说明求解字符s[i]的回文子串时，可以使用之前求出的结果。

（2）p[j] < mx - i ：说明以j为中心的回文子串全部在以id中心的势力范围内

此时，p[i] = p[j] ：i与j对称，则以i为中心的回文子串全部在以id中心的势力范围内。

此时，不会更新id和mx值，即可以直接处理下一个字符。

-------------------------------

第二种情况：

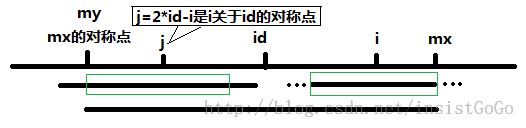
当 P[j] >= mx - i 的时候，以S[j]为中心的回文子串不一定完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能老老实实去匹配了。

------------------------------

说明：

在图中，具体包含两种情况：

（1）mx > i : 说明求解字符s[i]的回文子串时，可以使用之前求出的结果。

<1> p[j] > mx - i ：说明以j为中心的回文子串只有部分在以id中心的势力范围内

此时，p[i] = mx - i 且 不会更新id和mx值，即可以直接处理下一个字符。

<2> p[j] = mx - i ：说明以j为中心的回文子串全部在以id中心的势力范围内

此时，p[i] >= mx - i,即字符s[i]的回文子串向右至少会扩张到mx的位置，即之后还需要继续匹配。

至于这两种情况，可以在图上画画就可以推出。

-------------------------------

第三种情况：

对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了。

此时，正在处理的字符不在以id为起点的势力区间范围内，则无法用到上一次处理的结果，此时只能乖乖自己去匹配了。

于是代码如下：

 //输入，并处理得到字符串s
 int p[1000], mx = 0, id = 0;
 memset(p, 0, sizeof(p));
 for (i = 1; s[i] != '\0'; i++)
 {
     if (mx > i) //字符i在id的势力范围内，可以利用之前的结果。
     {
         p[i] = min(p[2*id-i], mx-i);
     }
     else //字符i不在id的势力范围内，只能挨着匹配。
     {
         p[i] = 1;
     }
     //挨着匹配
     while (s[i + p[i]] == s[i - p[i]])
     {
         p[i]++;
     }
     //更新id和其区间
     if (i + p[i] > mx)
     {
         mx = i + p[i];
         id = i;
     }
 }
 //最后需要在非#中，找出p[i]中最大的，之后最大p[i] - 1就是所求。

根据上面的分析，可以细化程序：

(1) 当 mx > i 且 mx - i > p[j]时，

此时，p[i] = p[j] 且 不会更新mx和id，可以直接处理下一个字符。

(2) 当 mx > i 且 mx - i < p[j]时，

此时，p[i] = mx - i 且 不会更新mx和id，可以直接处理下一个字符。

当然，这两种情况肯定也不会满足while的条件s[i + p[i]] == s[i - p[i]]和if的条件i + p[i] > mx，只不过他相比之下会多两次判断。

回头看，一旦这样展开，也会多一次if判断，在下面的程序中，可以不展开了。这里只是为了更好地说明该程序。

细化后的代码如下：

 //输入，并处理得到字符串s
 int p[1000], mx = 0, id = 0;
 memset(p, 0, sizeof(p));
 for (i = 1; s[i] != '\0'; i++)
 {
     if (mx > i)//能借鉴之前的结果
     {
         if (p[2*id-i] < mx - i)
         {
             p[i] = p[j];
             continue;
         }
         else if (p[2*id-i] > mx - i)
         {
             p[i] = mx - i;
             continue;;
         }
         else
         {
             p[i] = mx - i;
         }
     }
     else
     {
         p[i] = 1; //回文子串长度等于本身
     }
     //挨个匹配
     while(pNewStr[i + p[i]] == pNewStr[i - p[i]])
     {
         p[i]++;
     }
     //扩展已经匹配的最远距离
     if (i + p[i] > mx)
     {
         mx = i + p[i];
         nId = i;
     }
 }
 //找出p[i]中最大的

代码：

 #include <iostream>
 #include <assert.h>
 using namespace std;

 char* InitStr(char* pStr)
 {
     assert(pStr != NULL);
     //填充字符
     int nCount = 0;
     int nLenOldStr = strlen(pStr);
     int nLenNewStr = (nLenOldStr << 1) + 3;//ab -> $#a#b#0
     char* pNewStr = new char[nLenNewStr];
     pNewStr[nCount++] = '$';
     for (int i = 0;i < nLenOldStr;i++)
     {
         pNewStr[nCount++] = '#';
         pNewStr[nCount++] = pStr[i];
     }
     pNewStr[nCount++] = '#';
     pNewStr[nCount] = '\0';

     return pNewStr;
 }

 int Manacher(char* pStr)
 {
     assert(pStr != NULL);
     int nId = 1;
     int nMx = 0;
     int j = 0;
     int nLongest = 0;
     char* pNewStr = InitStr(pStr);
     int nLenStr = strlen(pNewStr);
     int* p = new int[nLenStr];
     memset(p,0,sizeof(int) * nLenStr);
     for (int i = 1;pNewStr[i] != '\0';i++)
     {
         if (nMx > i)//能借鉴之前的结果
         {
             p[i] = min(p[(nId << 1) - i],nMx - i);//id = (i + j) >> 1;
         }
         else
         {
             p[i] = 1; //回文子串长度等于本身
         }
         //挨个匹配
         while(pNewStr[i + p[i]] == pNewStr[i - p[i]])
         {
             p[i]++;
         }
         //扩展已经匹配的最远距离
         if (i + p[i] > nMx)
         {
             nMx = i + p[i];
             nId = i;
         }
         //找出最大值匹配字符个数
         if (pNewStr[i] != '#')
         {
             nLongest = max(nLongest,p[i]);
         }
     }
     delete[] pNewStr;
     delete[] p;
     return nLongest - 1;
 }

 int main()
 {
     //char strArr[] = "122122212";
     char strArr[] = "12212221";
     cout<<Manacher(strArr)<<endl;
     system("pause");
     return 1;
 }