HLG 1375 The Active Leyni (快速幂,动态规划,矩阵乘法)
| Description |
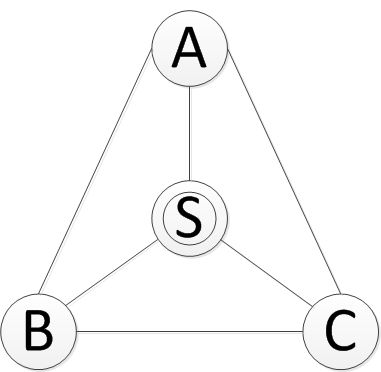
| There is a map of the town where Leyni lives. The vertex S indicates the home of Leyni and the vertexes A, B, C indicate the homes of his friends. They are connected to each other as the map presents. Leyni is too active that he can’t stay idle. It will count one step every time when he walks from one place to another. He starts from his home S and won’t stop. He wonders the number of ways in which he can go from his home S to itself in exactlyn steps. The number may be quite large, you should output it modulo 1000000007.
|
| Input |
| There are multiple test cases. The first line of input is an integerT indicating the number of test cases. Then T test cases follow. For each test case: Line 1. This line contains an integer n (1 ≤n ≤ 109) indicating the required steps. |
| Output |
| For each test case: Line 1. Output the number of ways modulo 1000000007. |
| Sample Input |
| 2 2 4 |
| Sample Output |
| 3 21 |
| Hint |
| In the first sample, the possible paths are: S=>A=>S S=>B=>S S=>C=>S |
顶点S代表Leyni的家,顶点A,B,C代表他的3个朋友的家,题中给出数n,Leyni从自家出发访问朋友经过n步再回到自己的家,问有多少不同的走法。
动态规划:
定义f[i][0]为走了i步恰好到达S的不同走法
定义f[i][1]为走了i步恰好到达A的不同走法
定义f[i][2]为走了i步恰好到达B的不同走法
定义f[i][3]为走了i步恰好到达C的不同走法
状态转换方程
f[i][0]=f[i-1][1]+f[i-1][2]+f[i-1][3]
f[i][1]=f[i-1][0]+f[i-1][2]+f[i-1][3]
f[i][2]=f[i-1][0]+f[i-1][1]+f[i-1][3]
f[i][3]=f[i-1][0]+f[i-1][1]+f[i-1][2]
数据量很大显然不能用纯粹的递推,递推一般数据较大时都是矩阵乘法,这道题的初始矩阵是A[1,0,0,0]即第0步到各个点的走法要乘的矩阵为一个只有对角线全为0,其他皆为1的矩阵.
走n步恰好到达S点的不同走法即使求A * Bn
using namespace std;
#define mod 1000000007
long long n;
void mul(long long A[][4],long long B[][4])
{
int i,j,k;
long long C[4][4]={0};
for(i=0;i<4;i++)
for(j=0;j<4;j++)
for(k=0;k<4;k++)
C[i][j]=C[i][j]+((A[i][k]%mod)*(B[k][j]%mod))%mod;
for(i=0;i<4;i++)
for(j=0;j<4;j++)
A[i][j]=C[i][j]%mod;
}
{
while(n)
{
if(n&1)
mul(A,B);
mul(B,B);
n=n/2;
}
cout<<A[0][0]<<endl;
}
int main()
{
int T;
cin>>T;
while(T--)
{
cin>>n;
long long A[4][4]={{1,0,0,0},{0,0,0,0},{0,0,0,0},{0,0,0,0}};
long long B[4][4]={{0,1,1,1},{1,0,1,1},{1,1,0,1},{1,1,1,0}};
martix(A,B);
}
return 0;
}