【学习点滴-数据结构-二叉树】二叉查找树源码实现
二叉排序数相关总结:
二叉排序树属于动态查找表,是一棵完全二叉树。它的性质为:
或者是一个空树,或者满足:
1.如果左子树不空,那么左子树所有节点的值都小于根节点的值。
2.如果右子树不空,那么右子树所有节点的值都大于根节点的值。
3.它的左右子树也分别是一个二叉查找树。可以看出,二叉查找树是一个递归的定义(树本身就是递归的定义。)
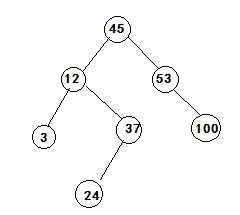
如下图示,就是一个简单的二叉查找树:
根据二叉排序树的定义我们知道,如果中序遍历之,那么得到的一定是一个递增有序的数列。(可反证之)。
二叉排序树用于查找,其过程类似于二分查找:先是根节点与待查找的key比较,如果相等,返回根节点。否则根据相应的大小关系递归地在左(右)子树中继续查找,直到查找成功或者查找失败返回。
相应的查找算法描述如下:
//在二叉查找树T中查找值为k的节点
Node *BsTreeSearch(BsTree T, int k){
if(T == NULL || k == T->key){
return T;
}
if(k < T->key){
return BsTreeSearch(T->lchild, k);
}
else{
return BsTreeSearch(T->rchild, k);
}
}二叉排序树作为一个“动态查找表”。其需要实现的基本操作包括:
1. Node *BsTreeSearch(BsTree T, int k) ==>查找特定等于k的节点 2. Node * BSTreeMinimum(BsTree T) ==>查找最小值 3. Node * BSTreeMaxMum(BsTree T) ==>查找最大值 4. void BsTreeInsert(BsTree &T, int k) ==>插入值为k的新节点 5. Node *BsTreeDelete(BsTree &T,Node *z) ==>删除节点并返回被删除的节点 当然,为了实现这些操作,我们还可以实现(不是必须) 6. Node *BSTreeSuccessor(Node *x) ==>查找节点的后继节点 7. Node *BSTreePrecessor(Node *x) ==>查找节点的前驱结点下面一个个进行分析总结:
1.查找,见上面的查找算法。不再赘述。
2.查找最小值。
由于二叉查找树的性质。值最小的节点一定是最左边的节点。我们沿着根节点一直走到最左边。找到的就是最小值的节点。(这也可以很清晰的从二叉查找树的图中看出)
算法很简洁,无需多解释:
//查找二叉查找树的最小结点
Node * BSTreeMinimum(BsTree T){
Node *x = T;
while(x->lchild != NULL){
x = x->lchild;
}
return x;
}
3.查找最大值。
与查找最小值对应。值最大的节点一定是最右边的节点,我们沿着根节点一直走到最右边。找到的就是最大值的节点。
//查找二叉查找树的最大结点
Node * BSTreeMaxMum(BsTree T){
Node *x = T;
while(x->rchild != NULL){
x = x->rchild;
}
return x;
}
4.先跳过二叉树插入和删除的部分。先看如何求节点的前驱和后继。
a. 节点的前驱:根据定义,前驱节点是中序遍历二叉查找树时位于该节点的正前边的一个节点。这里有几种情况:
<1>.如果节点有左子树。那么前驱一定位于左子树中,且是左子树的最大节点
如图所示(45节点的前驱为左子树的最大值37):
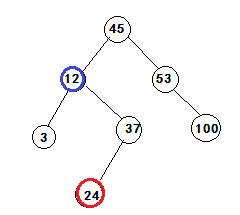
<2>.节点没有左子树。那么节点的前驱应该是中序遍历二叉查找树的直接前驱。这个前驱是谁呢?看下图:24号节点的前驱是哪个节点(往前找第一个比24小的节点)?
我们可以这样找,指针不停的向上移动 (即node *y = x->parent),直到x是y的右子树为止(因为如果是左子树,父节点只能位于该节点的后边,不可能是前驱)。
则相应的算法如下:
//查找二叉查找树某结点的前驱结点
Node *BSTreePrecessor(Node *x){
if(x->lchild != NULL)
return BSTreeMaxMum(x->lchild);
Node *y = x->parent;
while(y != NULL && x == y->lchild){
x = y;
y = y->parent;
}
return y;
}
b. 节点的后继:根据定义,后继节点是中序遍历二叉查找树时位于该节点的正后边的一个节点。这里有几种情况:
<1>.如果节点有右子树。那么后继一定位于右子树中,且是左子树的最小节点
<2>如果节点没有右子树。与查找前驱类似。指针不停的向上移动 (即node *y = x->parent),直到x是y的左子树为止(因为如果是右子树,父节点只能位于该节点的前边,不可能是后继)。
//查找二叉查找树某结点的后继结点
Node *BSTreeSuccessor(Node *x){
if(x->rchild != NULL)
return BSTreeMinimum(x->rchild);
Node *y = x->parent;
while(y != NULL && x == y->rchild){
x = y;
y = y->parent;
}
return y;
}
5.二叉查找树的插入。
建立一个二叉查找树的过程就是不断寻找插入为止,然后插入新节点的过程。插入删除是实现动态查找的前提。
二叉查找树的插入过程为:确定插入位置,插入新的节点。关键在于:如何确定插入位置。其实确定插入位置的过程,类似与二叉查找树的查找过程。
首先是与根进行比较,如果比根小,那么位于左子树中,否则位于右子树中。查找的过程中记录节点的父节点。一旦发现节点为空,那么父节点就是待插入节点的父节点(当然如果父节点为空,则树为空,此时只需要简单的令根节点等于插入的新节点即可)。然后判断是左子树还是右子树即可。
相应的代码实现如下:
//二叉查找树插入某个结点。
void BsTreeInsert(BsTree &T, int k){
Node *y = NULL;
Node *x = T;
Node *z = new Node;
z->key = k;
z->lchild = z->parent = z->rchild = NULL;
while(x != NULL){
y = x;
if(k < x->key)
x = x->lchild;
else
x = x->rchild;
}
z->parent = y;
if(y == NULL){
T = z;
}
else if(k < y->key)
y->lchild = z;
else
y->rchild = z;
}
6.二叉查找树的删除。
这是二叉查找树的难点。如果不画图的话,比较难于理解。
需要注意的是删除一个节点分为几个情况:
1.如果节点没有左子树也没有右子树,那么狠简单,直接删除即可。
2.如果节点有左子树但是没有右子树。那么删除节点后,令左子树变成父节点的左子树即可。
3.与2类似。如果节点有右子树但是没有左子树。那么删除节点后,令右子树变成父节点的右子树即可。
4.如果节点有左子树也有右子树。稍微麻烦一些。可以选择删除节点的前驱或者后继。查找前驱或后继的过程中记录父节点。删除前驱或后继节点后,连接原前驱或后继节点的左右子树即可。
算法导论上给出的算法如下:
Node *BsTreeDelete(BsTree &T,Node *z){
Node *x,*y;
if(z->lchild == NULL || z->rchild == NULL){
y = z;//y节点为最终实际删除的节点
}else{
y = BSTreeSuccessor(z);
}
if(y->lchild != NULL){
x = y->lchild;
}else{
x = y->rchild;
}
if(x != NULL){
x->parent = y->parent;
}
if(y->parent == NULL){
T = x;
}else if( y == y->parent->lchild){
y->parent->lchild = x;
}else{
y->parent->rchild = x;
}
if(y!=z){
z->key = y->key;//y节点为最终实际删除的节点,如果该节点不是z节点本身。那么需要将删除节点的值复制过来
}
return y;
}也可以根据这几种情况分别执行删除过程。可能更加容易理解一些。
完整的测试代码如下:
/* 二叉排序树的完整源码实现。
* 参考资料:1.严蔚敏==数据结构
* 2算法导论伪代码
* 3.http://www.wutianqi.com/?p=2430的总结)
*/
#include <iostream>
using namespace std;
typedef struct Node{
int key;
Node *lchild,*rchild,*parent;
}Node,*BsTree;
//查找二叉查找树的最小结点
Node * BSTreeMinimum(BsTree T){
Node *x = T;
while(x->lchild != NULL){
x = x->lchild;
}
return x;
}
//查找二叉查找树的最大结点
Node * BSTreeMaxMum(BsTree T){
Node *x = T;
while(x->rchild != NULL){
x = x->rchild;
}
return x;
}
//查找等于某值的结点。递归版本
Node *BsTreeSearch(BsTree T, int k){
if(T == NULL || k == T->key){
return T;
}
if(k < T->key){
return BsTreeSearch(T->lchild, k);
}
else{
return BsTreeSearch(T->rchild, k);
}
}
//查找二叉查找树某结点的后继结点
Node *BSTreeSuccessor(Node *x){
if(x->rchild != NULL)
return BSTreeMinimum(x->rchild);
Node *y = x->parent;
while(y != NULL && x == y->rchild){
x = y;
y = y->parent;
}
return y;
}
//查找二叉查找树某结点的前驱结点
Node *BSTreePrecessor(Node *x){
if(x->lchild != NULL)
return BSTreeMaxMum(x->lchild);
Node *y = x->parent;
while(y != NULL && x == y->lchild){
x = y;
y = y->parent;
}
return y;
}
//二叉查找树插入某个结点。
void BsTreeInsert(BsTree &T, int k){
Node *y = NULL;
Node *x = T;
Node *z = new Node;
z->key = k;
z->lchild = z->parent = z->rchild = NULL;
while(x != NULL){
y = x;
if(k < x->key)
x = x->lchild;
else
x = x->rchild;
}
z->parent = y;
if(y == NULL){
T = z;
}
else if(k < y->key)
y->lchild = z;
else
y->rchild = z;
}
Node *BsTreeDelete(BsTree &T,Node *z){
Node *x,*y;
if(z->lchild == NULL || z->rchild == NULL){
y = z;
}else{
y = BSTreeSuccessor(z);
}
if(y->lchild != NULL){
x = y->lchild;
}else{
x = y->rchild;
}
if(x != NULL){
x->parent = y->parent;
}
if(y->parent == NULL){
T = x;
}else if( y == y->parent->lchild){
y->parent->lchild = x;
}else{
y->parent->rchild = x;
}
if(y!=z){
z->key = y->key;
}
return y;
}
void visit(Node *x){
if(x != NULL){
printf("%d\n",x->key);
}
}
void InTraverse(BsTree T){
if(T != NULL){
InTraverse(T->lchild);
visit(T);
InTraverse(T->rchild);
}
}
int main(){
int m;
BsTree T = NULL;
while(scanf("%d",&m)!=EOF){
BsTreeInsert(T, m);
printf("二叉查找树中序遍历:");
InTraverse(T);
printf("\n");
}
printf("删除左结点后:");
BsTreeDelete(T, T->lchild);
InTraverse(T);
}
性能:二叉查找树树执行查找的时间与树的深度成正比,即log(n)数量级,在最坏的情况下,二叉查找树可能退化成线性链表,此时二叉查找树的查找时间为O(n),与顺序表一样。