joj1020 u Calculate e 输出精度设置

题目链接： http://acm.jlu.edu.cn/joj/showproblem.php?pid=1020

大致题意：

输出n由0到9的对应n e值

Sample Output

n e
- -----------
0 1
1 2
2 2.5
3 2.666666667
4 2.708333333

第一次我的程序， WA

#include "iostream"
#include <iomanip>
using namespace std;
int main(){
	cout<<"n e"<<endl
		<<"- -----------"<<endl;
	cout<<"0 1"<<endl;
	int i = 1;
	double jie = 1.0, e = 1.0;
	while(i <= 9){
		//上次的阶乘以i就是i的阶乘
		jie = jie * i;
		//上次的结果加 1 / jie就是这一次的结果
		e = e + 1 / jie;
		cout<<setprecision(10)<<i<<" "<<e<<endl;
		i++;
	}
	return 0;
}

运行结果：， 我以为会成功结果，跟他们AC结果不一样

AC的结果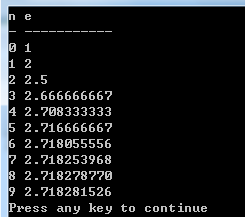：， 不一样在于8那里我没有输出最后一个0， 省略了，说实在鬼知道，2.5都不输出后面的0

正确程序:

#include "iostream"
#include <iomanip>
using namespace std;
int main(){
	cout<<"n e"<<endl
		<<"- -----------"<<endl;
	cout<<"0 1"<<endl;
	int i = 1;
	double jie = 1.0, e = 1.0;
	while(i <= 9){
		jie = jie * i;
		e = e + 1 / jie;
		if(i < 3)
			cout<<i<<" "<<e<<endl;
		else 
			cout<<setprecision(9)<<i<<" "<<fixed<<e<<endl;
		i++;
	}
	return 0;
}

补充精度控制的知识:

showpos    正数前面加上+号
fixed 使用小数计数法
scientific 使用科学计数法
uppercase 使用大写字符
showbase  显示数字的进制
boolalpha    bool值使用字符表示 , true或者false
noboolalpha     bool使用0和1表示
left   靠左对齐
right  靠右对齐
internal 字符靠左对齐, 数字卡右对齐

#include <iostream>  
#include <iomanip>  
using namespace std;  
  
int main( void )  
{  
    const double value = 12.3456789;  
    cout << value << endl;                    // 默认以6精度(6位有效数字)，所以输出为 12.3457  
    cout << setprecision(6) << value << endl; // 改成6精度，所以输出为12.3457    
    cout <<fixed;			     //加了fixed意味着是固定点方式显示，所以这里的精度指的是小数位
    cout << value << endl;                   // 固定以小数点后6位的形式输出，为0也会显示，这里输出12.345679  
    cout <<setprecision(4)<<value << endl;   // fixed的作用还在，依然显示12.3457
    cout <<value<<endl;			     //这个值同上12.3457
    cout.unsetf( ios::fixed );		     // 去掉了fixed，所以精度恢复成整个数值的有效位数，前面4精度，所以现在显示为12.35  
    cout << value << endl;  
    cout.precision( 6 );                     // 精度设置为6位有效数字，输出为12.3457  
    cout << value << endl;  
    cout<<fixed<<value<<endl;		    //以固定小数点精度输出，前面精度是6位所以这里输出12.345679
    return 0;
}

下面来自http://www.cplusplus.com/reference/ios/fixed/

Example

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

// modify floatfield #include <iostream> // std::cout, std::fixed, std::scientific int main () { double a = 3.1415926534; double b = 2006.0; double c = 1.0e-10; std::cout.precision(5); std::cout << "default:\n"; std::cout << a << '\n' << b << '\n' << c << '\n'; std::cout << '\n'; std::cout << "fixed:\n" << std::fixed; std::cout << a << '\n' << b << '\n' << c << '\n'; std::cout << '\n'; std::cout << "scientific:\n" << std::scientific; std::cout << a << '\n' << b << '\n' << c << '\n'; return 0; }

Possible output:

default: 3.1416 2006 1e-010 fixed: 3.14159 2006.00000 0.00000 scientific: 3.14159e+000 2.00600e+003 1.00000e-010