Assembly Intro - An Introduction to the SSE Instruction Set

http://neilkemp.us/src/sse_tutorial/sse_tutorial.html

Intel SSE Tutorial : An Introduction to the SSE Instruction Set


Table of Contents

+ Introduction, Prerequisites, and Summary

+ SSE Introstructions

+ Example 1: Adding Vectors

+ Shuffling

+ Example 2: Cross Product

+ Introduction to Intrinsics

+ Example 3: Multiplying a Vector

+ Source Code

+ SSE Links

Introduction, Prerequisites, and Summary

I am writing this tutorial on SSE (Streaming SIMD Extensions) for three reasons. First there is a lack of well organized tutorials for the subject matter, second it's an educational process I'm personally undertaking to better familiarize myself with low level optimization techniques, and finally what better way to have fun than to mess around with a bunch of registers!?

There are some things you should already be familiar with in order to benefit from this tutorial. For starters you should have a general understanding of computer organization, the Intel x86 architecture and it's assembly language, and a solid understanding of C++. These tutorials are mostly concerned with SSE optimizations of common graphics operations, so a good understanding of 3D math will also be useful.

Being a 3D graphics programmer I am always interested in learning ways to make my applications run at faster speeds. Common sense holds that the fewer CPU operations executed between each frame, the more frames my application can draw per second. 3D math is one area that will greatly benefit from SSE optimization as matrix transformations and vector calculations (ex. dot and cross product) generally eat up valuable CPU cycles. So the focus of this tutorial will mostly be directed at building optimized 3D math functions to use with graphics applications. This tutorial will introduce the instruction set by solving common vector operations. So without further ado let's have a look at the fun packed world of SSE.

SSE Introstructions

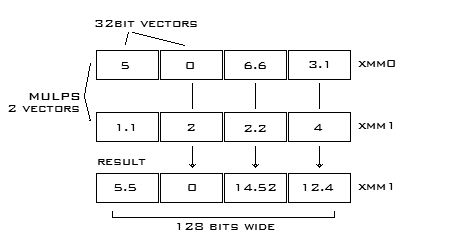
First what the heck is SSE? Basically SSE is a collection of 128 bit CPU registers. These registers can be packed with 4 32 bit scalars after which an operation can be performed on each of the 4 elements simultaneously. In contrast it may take 4 or more operations in regular assembly to do the same thing. Below you can see two vectors (SSE registers) packed with scalars. The registers are multiplied with MULPS which then stores the result. That's 4 multiplications reduced to a single operation. The benefits of using SSE are too great to ignore.

For a more detailed description of SSE you should read this article. It will give you a more thorough introduction to SIMD.

Now with the basic idea of SSE in mind let's take a look at some of the more common instructions.

Data Movement Instructions:

MOVUPS - Move 128bits of data to an SIMD register from memory or SIMD register. Unaligned.
MOVAPS - Move 128bits of data to an SIMD register from memory or SIMD register. Aligned.
MOVHPS - Move 64bits to upper bits of an SIMD register (high).
MOVLPS - Move 64bits to lowe bits of an SIMD register (low).
MOVHLPS - Move upper 64bits of source  register to the lower 64bits of destination register.
MOVLHPS - Move lower 64bits of source register  to the upper 64bits of destination register.
MOVMSKPS = Move sign bits of each of the 4 packed scalars to an x86 integer register.
MOVSS - Move 32bits to an SIMD register from memory or SIMD register.

Arithmetic Instructions:

A scalar  will perform the operation on the first elements only. The parallel version will perform the operation on all of the elements in the register.

Parallel        Scalar
ADDPS       ADDSS - Adds operands
SUBPS        SUBSS - Subtracts operands
MULPS       MULSS - Multiplys operands
DIVPS         DIVSS - Divides operands
SQRTPS      SQRTSS - Square root of operand
MAXPS      MAXSS - Maximum of operands
MINPS        MINSS - Minimum of operands
RCPPS         RCPSS - Reciprical of operand
RSQRTPS   RSQRTSS - Reciprical of square root of operand

Comparison Intstruction:

Parallel        Scalar
CMPPS       CMPSS - Compares operands and return all 1s or 0s.

Logical Instructions:

ANDPS - Bitwise AND of operands
ANDNPS - Bitwise AND NOT of operands
ORPS - Bitwise OR of operands
XORPS - Bitwise XOR of operands

Truth Table:

Destination	Source	ANDPS	ANDNPS	ORPS	XORPS
1	1	1	0	1	0
1	0	0	0	1	1
0	1	0	1	1	1
0	0	0	0	0	0

 

Shuffle Instructions:

SHUFPS - Shuffle numbers from one operand to another or itself. - See Shuffling for more details.
UNPCKHPS - Unpack high order numbers to an SIMD register.
UNPCKLPS - Unpack low order numbers to a SIMD register.

Other instructions that are not covered here include data conversion between x86 and MMX registers, cache control instructions, and state management instructions. To learn more details about any of these instructions you can follow one of the links provided at the bottom of this page.

Example 1: Adding Vectors

Now that we are more familiar with the instruction palette lets take a look at our first example. In this example we will add two 4 element vectors using a C++ function and inline assembly. I'll start by showing you the source and then explain each step in detail.

// A 16byte = 128bit vector struct
struct Vector4
{   
        float x, y, z, w;       
};

// Add two constant vectors and return the resulting vector
Vector4 SSE_Add ( const Vector4 &Op_A, const Vector4 &Op_B )
{
        Vector4 Ret_Vector;

        __asm
        {       
                MOV EAX Op_A                              // Load pointers into CPU regs
                MOV EBX, Op_B

                MOVUPS XMM0, [EAX]                 // Move unaligned vectors to SSE regs
                MOVUPS XMM1, [EBX]

                ADDPS XMM0, XMM1                   // Add vector elements
                MOVUPS [Ret_Vector], XMM0      // Save the return vector
        }

        return Ret_Vector;
}

Because we are sending references to the function rather than copies as parameters we will need to move the vector pointers to 32bit registers EAX and EBX first. Using the MOVUPS for unaligned data, we move the literal values of the 32bit registers into SIMD registers XMM0 and XMM1. Next we use ADDPS on to add the register operands and store the resulting vector in XMM0. The final step is to move the contents of XMM0 to a vector structure before returning it. Once again we use MOVUPS to do so.

So that doesn't look so hard. We have an unaligned 4 element vector to send to and get from the addition function. I said that the vector is unaligned but what does that mean? To be more specific the vector is not guaranteed to be a 16 byte aligned struct. Huh? The SSE registers are each 128 bits or 16 bytes. If data in memory has a 16 byte border then it is said to be aligned data. What this means is that the data will start on a 16 byte boundary in memory. In this case we are doing nothing special to the data to guarantee the 16 byte alignment. In later examples we will see how to manually align data. Some compilers, such as the Intel compiler, will automatically align the data during compilation. It should be noted that using aligned data is much faster than using unaligned data.

Shuffling

Shuffling is an easy way to change the order of a single vector or combine the elements of two separate registers. The SHUFPS instruction takes two SSE registers and an 8 bit hex value. The first two elements of the destination operand are overwritten by any two elements of the destination register. The third and fourth elements of the destination register are overwritten by any two elements from the source register. The hex string is used to tell the instruction which elements to shuffle. 00, 01, 10, and 11 are used to access elements within the registers.

Examples:

SHUFPS XMM0, XMM0, 0x1B       // 0x1B =  00 01 10 11 and reverses the order of the elements

SHUFPS XMM0, XMM0, 0xAA     // 0xAA = 10 10 10 10 and sets all elements to the 3rd element

Example 2: Cross Product

Here is a common 3D calculation to find the normal of two vectors. It demonstrates a useful way of shuffling register elements to achieve optimal performance.

// R.x = A.y * B.z - A.z * B.y
// R.y = A.z * B.x - A.x * B.z
// R.z = A.x * B.y - A.y * B.x

// Find the cross product of two constant vectors and return it.

Vector4 SSE_CrossProduct(const Vector4 &Op_A, const Vector4 &Op_B)
{
        Vector4 Ret_Vector;
        __asm
        {
                MOV EAX Op_A                               // Load pointers into CPU regs
                MOV EBX, Op_B

                MOVUPS XMM0, [EAX]                 // Move unaligned vectors to SSE regs
                MOVUPS XMM1, [EBX]   
                MOVAPS XMM2, XMM0               // Make a copy of vector A
                MOVAPS XMM3, XMM1               // Make a copy of vector B

                SHUFPS XMM0, XMM0, 0xD8      // 11 01 10 00  Flip the middle elements of A
                SHUFPS XMM1, XMM1, 0xE1       // 11 10 00 01 Flip first two elements of B
                MULPS  XMM0, XMM1                 // Multiply the modified register vectors
               
                SHUFPS XMM2, XMM2, 0xE1      // 11 10 00 01 Flip first two elements of the A copy
                SHUFPS XMM3, XMM3, 0xD8     // 11 01 10 00  Flip the middle elements of the B copy
                MULPS XMM2, XMM3                 // Multiply the modified register vectors
              
                SUBPS  XMM0, XMM2                  // Subtract the two resulting register vectors
              
                MOVUPS [Ret_Vector], XMM0      // Save the return vector
        }
        return Ret_Vector;
}

Introduction to Intrinsics

Rather than redefine what an intrinsic is, I'll just quote from the MSDN.

"An intrinsic is a function known by the compiler that directly maps to a sequence of one or more assembly language instructions. Intrinsic functions are inherently more efficient than called functions because no calling linkage is required.

Intrinsics make the use of processor-specific enhancements easier because they provide a C/C++ language interface to assembly instructions. In doing so, the compiler manages things that the user would normally have to be concerned with, such as register names, register allocations, and memory locations of data." - MSDN

In short we no longer need to use the inline assembly mode when using SSE with our C++ applications and we no longer need to worry about register names. Working with intrinsics is somewhere between assembly programming and high level programming. Let's take a look at how to use them with what we already know.

Example 3: Multiplying a Vector

Here is an example of multiplying a vector by a floating point scalar. It uses an intrinsic function to initialize a 128 bit object.

// Multiply a constant vector by a constant scalar and return the result

Vector4 SSE_Multiply(const Vector4 &Op_A, const float &Op_B)
{
        Vector4 Ret_Vector;

        __m128 F = _mm_set1_ps(Op_B)             // Create a 128 bit vector with four elements Op_B
       
        __asm
        {       
                MOV EAX, Op_A                               // Load pointer into CPU reg

                MOVUPS XMM0, [EAX]                   // Move the vector  to an SSE reg      
                MULPS XMM0, F                               // Multiply vectors
                MOVUPS [Ret_Vector], XMM0       // Save the return vector
        }
        return Ret_Vector;
}

What we see here is the use of a 128 bit object F which is set using an a memory initialization intrinsic called _mm_set1_ps( float ). This sets all four elements of F to a floating point value. We can then use this 128 bit object with our SSE assembly code.

There are many more intrinsics which can greatly simplify SSE development. Check out the MSDN for a complete reference of intrinsics.


Source Code

The source code and html for this tutorial can be downloaded here. It demonstrates vector operations using SSE and inline assembly.

Because inline assembly is used in the examples the source will not compile with the x64 Visual C++ compiler.

SSE Links


MSDN

Tommesani Docs