2015年04月02日阿里笔试总结
每次写简历的时候感觉自己很牛逼,每次面试和笔试的时候,却发现自己很搓逼![]() ,今天阿里笔试再次被鄙视!感觉要学的东西太多了啊。
,今天阿里笔试再次被鄙视!感觉要学的东西太多了啊。
1. 函数lg(ax^2-8x+a-6)的值域为R,那么实数a的取值范围为
A. [0, 8] B.[-2, 8]C. (0, 8]D.(-2, 8]E.(-2, +无穷)F.[8, +无穷)
尼玛,这不是高中的题目吗?全忘了有不有?静下心来分析一下,函数的值域为R,那么ax^2-8x+a-6的值域肯定要包含(0, +无穷大)。这里要分一次函数还是二次函数,若a=0,有ax^2-8x+a-6=-8x-6,值域包括(0, +无穷大),可行。若a!=0,那么二次函数y=ax^2-8x+a-6开口要向上,且最低点要小于等于0。那么a>0且最低点x=-b/2a要小于等于0。于是乎,有a*(4/a)^2-8*(4/a)+a-6<=0,得出:0<a<=8,又因为a能够等于0,因此结果是[0, 8],跪了有不有?谁还记得最低点是-b/2a呢?
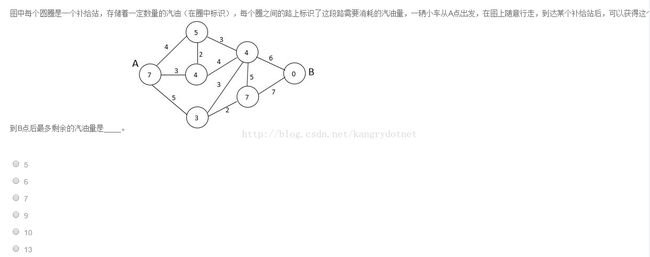
2. 题目如下所示:
这道题类似于最短路径啊,将图转化成加油图,如下所示,每条边表示从一个顶点到另外一个顶点赚的油数。然后找出从A到B最大路径。最后分析,从A到4-》5-》4-》3-》2-》0加的油最多,为最后剩下10。
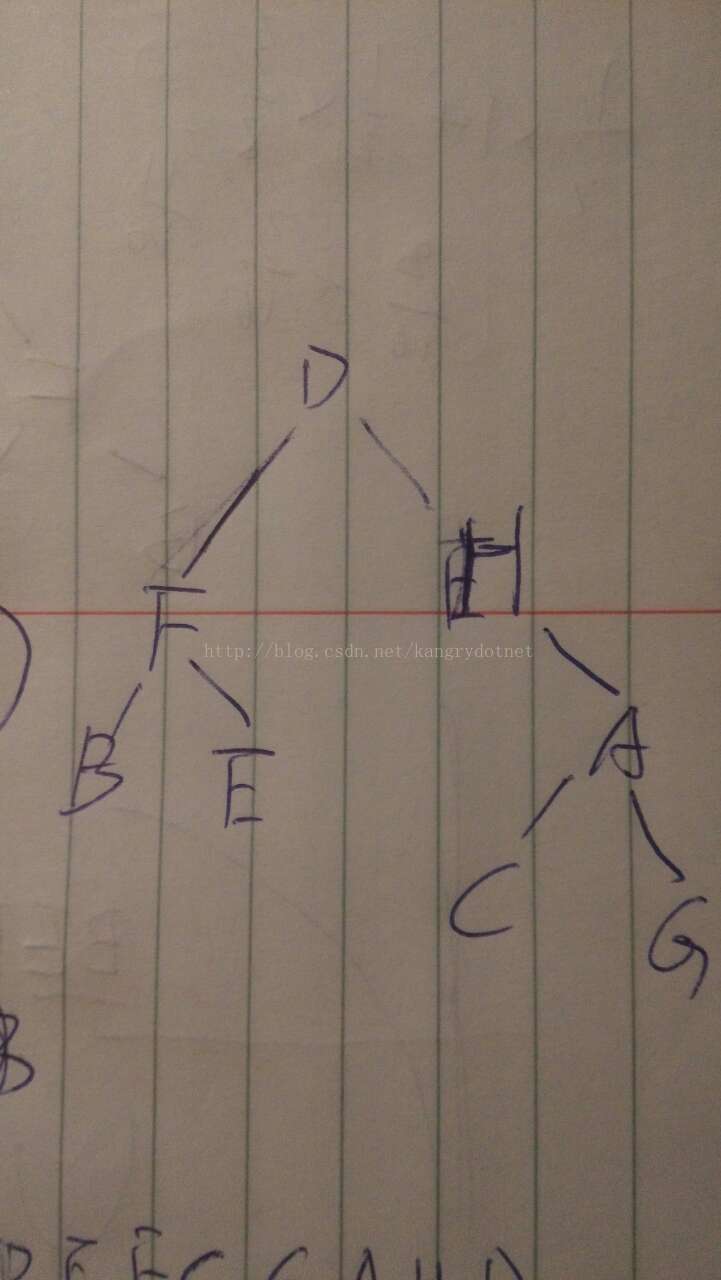
3. 已知某二叉树的前序遍历为‘DFBEHACG’,中序遍历为‘BFEDHCAG’,则后序遍历为:
思想:通过前序遍历得到根节点,中序遍历得到左右孩子,如此递归。例如,前序第一个为D,在中序遍历中,D前面的BFE为左孩子,后面的HCAG为右孩子节点。FBE和BFE又是左孩子的先序遍历和中序遍历,如此递归找下去,得到的二叉树为下图所示。因此后序遍历为:BEFCGAHD
4. 用十进制计算30!(30的阶乘),将结果转化成3进制进行表示的话,该进制下的结果末尾会有多少个0?
先看10进制中10!后有多少个0的问题是如何计算的。注意到10的质因数为2和5,将10!每个因数分解成质因数的形式,每对2和5贡献一个0,共有两对2和5,因此,10的阶乘后面有2个0。同理,对于3进制,3的质因数为3,将30!的每个因子分解成质因数的形式,末尾0的个数就是质因数的3的个数。我们只考虑3的倍数,3、6、12、15、21、24、30每个数贡献1个3,9、18贡献2个3,27贡献个3,因此质因数3的个数为1*7+2*2+3*1=14个。
5. 现在有50个红球,50个篮球,给小明两个袋子,一个袋子能装任意个球(0-100)。先由小明将这100个球以一定的方法装入这两个袋子。找到一个不明真相的路人,闭眼,随机从两个袋子中随机选择一个袋子并摸出一个球。要是他摸出红球的概率最高,小明该如何分配?
A. 一个袋子放50个红球,另外一个袋子放50个篮球
B. 一个袋子20个红球,另一个袋子30个红球和50个蓝球
C. 一个袋子放25个红球和25个蓝球,另一个也放25个红球和25个蓝球
D. 一个袋子不放任何一个球,另外一个袋子放全部的球
E. 一个袋子放75个球(任意颜色),另外一个袋子放剩下的25个
F. 以上都不是最优解
我的答案是一个袋子放1个红球,另外一个袋子放剩下的99个球,抽出红球的概率是1/2+1/2*49/99。这样会不会概率最大?所以我选择F
6. 春节期间,甲乙丙三人用支付宝钱包玩发红包游戏,只能通过格子账户余额来发红包,第一轮甲给乙的红包金额等于乙支付宝钱包内账户余额,甲給丙的红包金额等于丙支付宝钱包内的账户余额,与此相同,第二轮乙给甲和丙的红包金额等于他们各自支付宝钱包的账户余额,第三轮丙给甲和乙的红包金额等于他们各自支付宝里面的账户余额。倘若大家最后支付宝钱包的余额均为16元,则甲最初的支付宝账户余额为:
这道题就是解方程组啊,设甲乙丙开始的账户余额为x、y、z,按题意可得出3个方程,解方程的x=26,y=14,z=8
7. 对于192.168.0.0到192.168.0.255这个网络来说,以下说法正确的是:
A. 网段内可用来作为主机IP的范围是:192.168.0.0到192.168.0.255
B. Network IP是192.168.0.255
C. Broadcase IP是192.168.0.0
D. 网段内的主机可以通过网卡对网卡传递数据
E. 192.168.0.1和192.168.0.2的主机需要使用router传递数据包
F. 是Class B等级
网络知识一直都不大明白,学习网络的时候基本上是混过来的。于是恶补了一下网络知识。192.168.0.0~192.168.0.255是C类ip地址中的私有地址部分。若其子网掩码为255.255.255.0,那么气网络ip为192.168.0.0,广播地址为192.168.0.255,主机能够分配的地址为192.168.0.1~192.168.0.254。router的作用是连接两个不同的网络,192.168.0.1和192.168.0.2是同一个网络,可以不经过路由。排除法,选D。
8. 有8只球队,采用抽签的方式随机配对,组成4场比赛。假设其中有3只强队,那么出现强强对话(任意两只强队相遇)的概率为:
可以看成8个场地,1和2号场地是一个球场,3和4号场地是一个球场,。。。,然后将8支球队安排在这8个场地中。不出现强强对话的情况是有:8*6*4,(这里只考虑强队的安放),共有安放的情况有8*7*6,于是出现强强对话的概率=1-(8*6*4)/(8*7*6)=3/7。
9. 已知某个哈希表的n个关键字具有相同的哈希值,如果使用二次探测再散列将这n个关键字存入哈希表,至少要进行多少次探测?
按博客http://blog.csdn.net/jnu_simba/article/details/9664053的说法,不管是一次探测还是二次探测,n个相同关键字最少的探测次数为(1+n)*n/2。存入第一个参数的探测次数为1,第二个为2,第三个为3,...,于是便有1+2+3+...+n
10. 设二叉树节点的先跟序列、中根序列和后根序列中,所有叶子节点的先后顺序:
先根序列、中根序列、后根序列只是根节点的出现顺序不一样,对于叶子节点,都是从左往右的,因此,三种序列的叶子节点先后顺序都是相同的,且从左往右。