计蒜之道 初赛 第一场 题解 dp 高效 网络流 最小割 最大流 ISAP 模板
搜狗输入法最近的用户输入中出现了一种新的输入模式,形如 “0k1234567”,搜狗的工程师发现这一模式后了解到,这是一种新被提出的对于十五进制数字的标记模式,其中 “0k” 是标记进制为15的前缀标记,之后的部分 “1234567” 是实际的十五进制的数字串。
在发现这一标记模式后,搜狗的工程师开始尝试在已有的分词算法上进一步加入对于十五进制数字串的处理,把网页上的这种形式的 15 进制数正确地提取出来。我们知道,标记十五进制的 “0k” 中 k 必须是小写,数字 0 到 14 在这套标记模式下会被依次表示为:0k0, 0k1, ..., 0k9, 0kA, 0kB, 0kC, 0kD, 0kE。也就是说 15 进制数字中只会出现 0-9、k 和 A-E。
值得注意的是,数字表示中不能有多余的 0,比如 0k05 是不能被当做一个十五进制数字的。另外,作为一种约定,当出现 “0k90k8” 时,只有 0k90 是符合期望的十五进制数字,即总是从左至右依次提取出最长的十五进制数字。如果希望表达 0k9 和 0k8 这两个数字的连写情况时,则会被写成 “0k9'0k8” 这一的形式(单引号代表其他任意非数字字符)。
搜狗的工程师希望将用户输入中符合上述要求的所有十五进制数依次输出。你能帮他实现么?
输入格式
输入一行字符串 str (1 ≤ |str| ≤ 106),表示搜狗工程师得到的用户输入。用户输入中的字符一定是数字 (0 - 9) 或大小写英文字母 (a - z, A - Z)。
输出格式
输出包括若干行,每行输出一个提取出的十五进制数(形式如同:0k1234),分别对应输入字符串中含有的若干个符合标记模式的十五进制数字;输出时,请以数字在原字符串中的顺序依次输出。
样例1
输入:
sjfjfhua0kA0000lmNhdhahdfhGgdJG90K10k110k120kF
输出:
0kA0000 0k110
#define N 1000050
#define M 100005
#define maxn 205
#define MOD 1000000000000000007
int n,len;
char str[N];
bool isNum(char c){
if(c >='0' && c<='9') return true;
if(c >='A' && c<='E') return true;
return false;
}
int main()
{
while(SS(str)!=EOF)
{
int st = -1,flag = 0;
len = strlen(str);
FI(len){
if(st != -1){
if(!flag){
if(str[i] == '0'){
printf("0k0\n");
st = -1;
flag = 0;
continue;
}
}
if(!isNum(str[i])){
if(flag){
for(int j = st;j<i;j++)
printf("%c",str[j]);
printf("\n");
}
st = -1;
}
flag++;
}
else if(st == -1 && str[i] == '0' && i <= len-1 && str[i+1] == 'k'){
st = i;i++;flag = 0;
}
}
if(st != -1 && flag){
for(int j = st;j<len;j++)
printf("%c",str[j]);
printf("\n");
}
}
return 0;
}
工作区的颜值选择(简单)
360硅谷范的工作区被划为了 n 行 m 列的连续工位,每个工位上可以安排一名员工工作。当第 i 行第 j 列(行和列都从1开始编号)的工位中坐着一个颜值为 C 的员工时,公司会需要付出的成本是 (|C + i + j| ⊕ U) * W(其中⊕是按位异或符号)。U 是这个工位的风水指数,W 是这个工位上接收到360安全路由发出的wifi信号强度。
比较有意思的是,两个相邻的工位(同行相邻列或同列相邻行)上坐着颜值为 C1 和 C2 的员工时,公司会额外付出 |C1 + C2| 的成本。
找到一种方案,决定每个工位上的员工应有的颜值 C (|C| ≤ k),使得公司最终需要付出的总成本最小。并输出需要付出的最小总成本。
输入格式
第一行输入三个整数 n, m, k (1 ≤ k ≤ 30) 分别表示工区的长、宽、和颜值绝对值的上限。
接下来读入两个 n 行 m 列的整数矩阵。
第一个矩阵表示每个工位的风水指数 Ui,j (1 ≤ Ui,j ≤ 30)。
第二个矩阵表示每个工位收到360安全路由发出的wifi信号强度Wi,j (1 ≤ Wi,j ≤ 30 且 Wi,j 为整数)。
对于简单版本,1 ≤ n ≤ 2,1 ≤ m ≤ 3;
对于中等版本,n = 2, 1 ≤ m ≤ 30;
对于困难版本,1 ≤ n, m ≤ 30。
输出格式
输出一个数,表示公司需要付出的最小成本。
样例1
输入:
2 2 2 1 0 1 0 1 1 1 1
输出:
11
提示信息
样例的填充方案如下:
-1 1
0 -1
使用的深搜,一个个试,加上了小小的剪枝,水平有限,只能过简单,复杂度是指数级的,如果有好的算法,希望指点下。
#define N 205
#define M 100005
#define maxn 205
#define MOD 1000000000000000007
int n,m,k;
int u[N][N],w[N][N],ans,vis[N][N],land[N][N],maxx[N][N];
int dir[2][2] = {{-1,0},{0,-1}};
bool isRight(int x ,int y){
if(x>=0 && x<n && y <m && y>=0) return true;
return false;
}
int CheckAns(int sum,int i,int j){
sum += (abs(land[i][j] + i + 1 + j + 1) ^ u[i][j]) * w[i][j];
for(int s = 0;s<2;s++){
int xx = i + dir[s][0],yy = j + dir[s][1];
if(isRight(xx,yy)){
sum += abs(land[i][j] + land[xx][yy]);
}
}
return sum;
}
int DFS(int x,int y,int sum){
if(sum > ans) return 0;
if(x == n-1 && y == m-1){
for(int i = -k ;i<=k;i++){
land[x][y] = i;
ans = min(CheckAns(sum,x,y),ans);
}
return 0;
}
for(int i = -k ;i<=k;i++){
land[x][y] = i;
if(y < m - 1) {
DFS(x,y + 1,CheckAns(sum,x,y));
}
else if(y == m - 1){
DFS(x+1,0, CheckAns(sum,x,y));
}
}
return 0;
}
int main()
{
while(S2(n,m)!=EOF)
{
S(k);
FI(n)FJ(m)S(u[i][j]),maxx[i][j] = INF;
FI(n)FJ(m)S(w[i][j]);
ans = 0;
FI(n){
FJ(m){
ans +=(( i + 1 + j + 1) ^ u[i][j]) * w[i][j];
}
}
DFS(0,0,0);
printf("%d\n",ans);
}
return 0;
}
解法二,
两个的时候,可以使用dp的方法
dp[i][x][y]表示,第 i位上为x 下为y的最小值,c[i][x][y]表示,第 i位上为x 下为y的花费。
则可得,状态转移方程 dp,i,x,y = dp ,i -1,a,b + abs(a+x) + abs(b+y) + cos i,x,y;
枚举a,b的话,复杂度为o(m * k ^4)会超时,用d[i][x][y] 表示,dp[i-1] [a][b] + abs(b+y)的最值,这样复杂度减为o(m * k ^3)也就能过中等数据了
#define N 100
#define M 50
#define maxn 205
#define MOD 1000000000000000007
int n,m,k;
int u[3][N],w[3][N],c[35][N][N],dp[35][N][N],d[35][N][N],ans;
int main()
{
while(S2(n,m)!=EOF)
{
S(k);
FI(n)FJ(m)cin>>u[i+1][j+1];
FI(n)FJ(m)cin>>w[i+1][j+1];
for(int i = 1;i<=m;i++){
for(int a = -k;a<=k;a++){
for(int b = -k;b <= k;b++){
int aa = a + M , bb = b + M;
c[i][aa][bb] = (abs(a + 1 + i) ^ u[1][i])*w[1][i] + (abs(b + 2 + i)^ u[2][i])*w[2][i] + abs(a + b);
dp[i][aa][bb] = INF;d[i][aa][bb] = INF;
}
}
}
for(int i = 1;i<=m;i++){
for(int x = -k;x<=k;x++){
for(int y = -k;y <= k;y++){
int xx = x + M,yy = y + M;
for(int a = -k;a<=k;a++){
int aa = a + M;
dp[i][xx][yy] = ( i > 1 ?
min(dp[i][xx][yy],d[i-1][aa][yy] + abs(a + x) + c[i][xx][yy]):
c[i][xx][yy] );
}
}
}
for(int x = -k;x<=k;x++){
for(int y = -k;y <= k;y++){
int xx = x + M,yy = y + M;
for(int b = -k;b<=k;b++){
int bb = b + M;
d[i][xx][bb] = min(d[i][xx][bb],dp[i][xx][yy] + abs(y + b));
}
}
}
}
ans = INF;
for(int x = -k;x<=k;x++){
for(int y = -k;y <= k;y++){
int xx = x + M,yy = y + M;
ans = min(ans,dp[m][xx][yy]);
}
}
cout<<ans<<endl;
}
return 0;
}
第三种方法,网络流的方法,
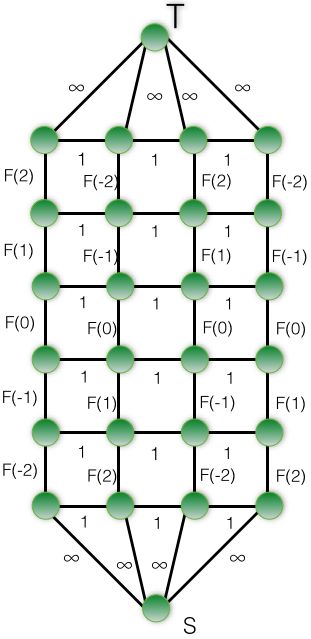
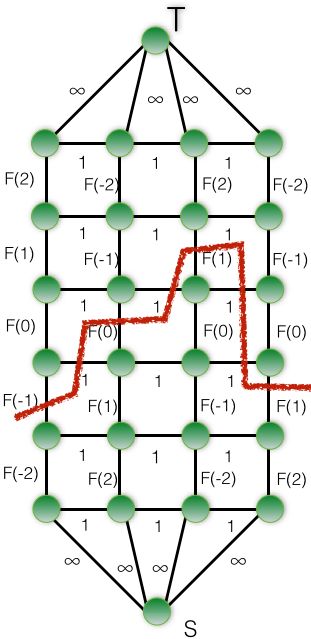
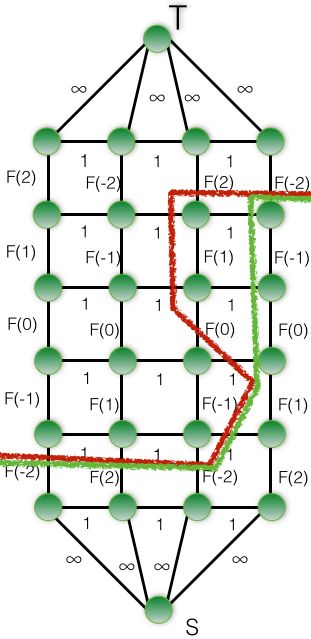
考虑如下建图
将每一个工位拆为 2k+2 个点,之间连权值为 F( i ) 的边,F( i ) 表示对应格点填 i 时的价值,相邻对应点连权值为 1 的边源点汇点分别连向链的末端权值 ∞,考虑一个割的情况
该割集对应的价值为
F(-1)+1+F(0)+1+F(1)+1+1+F(1)=
F(-1)+|-1+0|+F(0)+|0+1|+F(1)+|1+1|+F(1)
也就是一个割集对应一个解的价值,所以对上图求解最小割即可
要注意考虑到以下割集的情况
图中点数为 30×30×60 ,大概 5 万左右的点数,需要用效率较高的最大流算法才能通过所有测试数据
使用ISAP模板,可以过困难。#define N 100
#define M 100005
#define maxn 70000
#define MOD 1000000000000000007
int u[N][N],w[N][N],k,color[N][N];
int n,m,s,e,l;
int dir[2][2] = {{1,0},{0,1}};
struct Edge{
int from,to,cap,flow;
Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
struct EdmondsKarp{
int n,m;
vector<Edge> edges;//存边 边的两倍
vector<int> G[maxn];//邻接表,图
int a[maxn];//起点到i的可改进量
int p[maxn];//最短路入弧号
void init(int n){
FI(n) G[i].clear();
edges.clear();
}
void AddEdge(int from,int to,int cap){
edges.push_back(Edge(from,to,cap,0));
edges.push_back(Edge(to,from,0,0));//反向
m = edges.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
}
int Maxflow(int s,int t){
int flow = 0;
for(;;){
memset(a,0,sizeof(a));
queue<int> Q;
Q.push(s);
a[s] = INF;
while(!Q.empty()){
int x = Q.front();Q.pop();
FI(G[x].size()){
Edge & e = edges[G[x][i]];
if(!a[e.to]&&e.cap > e.flow){
p[e.to] = G[x][i];
a[e.to] = min(a[x],e.cap - e.flow);
Q.push(e.to);
}
}
if(a[t]) break;
}
if(!a[t]) break;
for(int u = t;u !=s;u = edges[p[u]].from){
edges[p[u]].flow += a[t];
edges[p[u] ^ 1].flow -= a[t];
}
flow += a[t];
}
return flow;
}
};
struct Dinic{
int n,m,s,t;
vector<Edge> edges;//存边 边的两倍
vector<int> G[maxn];//邻接表,图
bool vis[maxn];//BFS使用
int d[maxn];//起点到i的距离
int cur[maxn];//当前弧下标
void init(int nn){
n = nn;
FI(n) G[i].clear();
edges.clear();
}
void AddEdge(int from,int to,int cap){
edges.push_back(Edge(from,to,cap,0));
edges.push_back(Edge(to,from,0,0));//反向
m = edges.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
}
bool BFS(){
memset(vis,0,sizeof(vis));
queue<int> Q;
Q.push(s);
d[s] = 0;
vis[s] = 1;
while(!Q.empty()){
int x = Q.front();Q.pop();
for(int i=0;i<G[x].size();i++){
Edge & e = edges[G[x][i]];
if(!vis[e.to] && e.cap > e.flow){
vis[e.to] = 1;
d[e.to] = d[x] + 1;
Q.push(e.to);
}
}
}
return vis[t];
}
int DFS(int x,int a){
if(x == t || a== 0) return a;
int flow = 0,f;
for(int i= cur[x];i<G[x].size();i++){
Edge & e = edges[G[x][i]];
if(d[x] + 1 == d[e.to] && ( f= DFS(e.to,min(a,e.cap - e.flow)))>0){
e.flow += f;
edges[G[x][i]^1].flow -= f;
flow += f;
a -= f;
if( a== 0)break;
}
}
return flow;
}
int Maxflow(int s,int t){
this->s = s;this-> t = t;
int flow = 0;
while(BFS()){
memset(cur,0,sizeof(cur));
flow += DFS(s,INF);
}
return flow;
}
};
//EdmondsKarp Ek;
//ISAP 模板
const int mm=2000000;
const int mn=70000;
const int oo=1000000000;
struct ISAP{
int node,src,dest,edge;
int ver[mm],flow[mm],next[mm];
int head[mn],work[mn],h[mn],q[mn],gap[mn],p[mn],cur[mn];
void prepare(int _node,int _src,int _dest)
{
node=_node,src=_src,dest=_dest;
for(int i=0; i<node; ++i)head[i]=-1;
edge=0;
}
void init(int _node){
node=_node,src=1,dest=n;
for(int i=0; i<node; ++i)head[i]=-1;
edge=0;
}
void AddEdge(int u,int v,int c)
{
ver[edge]=v,flow[edge]=c,next[edge]=head[u],head[u]=edge++;
ver[edge]=u,flow[edge]=0,next[edge]=head[v],head[v]=edge++;
}
void Isap_Pre()
{
int i,u,v,l,r=0;
for(i=0; i<node; ++i)h[i]=gap[i]=0;//高度初始为0,汇点为1
h[q[r++]=dest]=1;
for(l=0; l<r; ++l)
for(i=head[u=q[l]]; i>=0; i=next[i])
if(flow[i^1]&&!h[v=ver[i]])
h[q[r++]=v]=h[u]+1;
for(i=0; i<node; ++i)++gap[h[i]];//统计高度个数
}
int Maxflow(int _src,int _dest){
src=_src,dest=_dest;
Isap_flow();
}
int Isap_flow()
{
int i,j,u,ret=0,tmp,minh,deep=0;
Isap_Pre();
for(i=0; i<node; ++i)work[i]=head[i];
p[0]=u=src,cur[0]=oo;
while(h[src]<=node)
{
if(u==dest)
{
tmp=cur[deep],deep=0,u=-1;
for(i=src;i!=dest;i=ver[j])
{
flow[j=work[i]]-=tmp,flow[j^1]+= tmp;
if(u<0)!flow[j]?u=i:cur[++deep]-=tmp;
}
ret+=tmp;
}
int &e=work[u];
for(;e>=0;e=next[e])
if(flow[e]&&h[u]==h[ver[e]]+1)break;
if(e>=0)
{
p[++deep]=u=ver[e];//栈记录节点
cur[deep]=min(cur[deep-1],flow[e]);//栈记录最大流量
continue;
}
if(--gap[h[u]]==0)break;
work[u]=head[u],minh=node;
for(i=head[u];i>=0;i=next[i])
if(flow[i])minh=min(minh,h[ver[i]]);
++gap[h[u]=max(h[u],minh)+1];//一定要比本身大否则gap优化会出错
if(deep>0)u=p[--deep];
}
return ret;
}
};
//Dinic Ek;
ISAP Ek;
bool isRight(int x ,int y){
if(x>=0 && x<n && y <m && y>=0) return true;
return false;
}
void AddEdge2(int x, int y,int xx,int yy){
int n1 = x * m + y,n2 = xx * m + yy,all = (n1 + 1) * l,kk = k;
for(int i = n1 * l,j = n2 * l;i < all;i++,j++){
Ek.AddEdge(i,j,1);
Ek.AddEdge(j,i,1);
}
}
int getKv(int i,int j,int kk){
return (abs( kk + i + 1 + j + 1) ^ u[i][j]) * w[i][j];
}
void AddEdge1(int x, int y){
int n1 = x * m + y,all = (n1 + 1) * l;
if(color[x][y]){
for(int i = n1 * l,kk = k;i < all - 1;i++,kk--){
Ek.AddEdge(i,i+1,getKv(x,y,kk));
Ek.AddEdge(i+1,i,getKv(x,y,kk));
}
}
else {
for(int i = n1 * l,kk = -k;i < all - 1;i++,kk++){
Ek.AddEdge(i,i+1,getKv(x,y,kk));
Ek.AddEdge(i+1,i,getKv(x,y,kk));
}
}
Ek.AddEdge(s,n1 * l,oo);
Ek.AddEdge(all - 1,e,oo);
}
int main()
{
while(S2(n,m)!=EOF)
{
fill(color,-1);
color[0][0] = 1;
FI(n){
FJ(m){
for(int a = 0;a<2;a++){
int ii = i + dir[a][0],jj = j + dir[a][1];
if(isRight(ii,jj) && (color[ii][jj] == -1) ){
color[ii][jj] = color[i][j] ^ 1;
}
}
}
}
S(k);
FI(n)FJ(m)S(u[i][j]);
FI(n)FJ(m)S(w[i][j]);
l = 2 * k + 2;
s = n * m * l ; e = n * m * l + 1;
Ek.init(n * m * l + 3);
FI(n){
FJ(m){
AddEdge1(i,j);
for(int a = 0;a<2;a++){
int ii = i + dir[a][0],jj = j + dir[a][1];
if(isRight(ii,jj)){
AddEdge2(i,j,ii,jj);
}
}
}
}
printf("%d\n",Ek.Maxflow(s,e));
}
return 0;
}