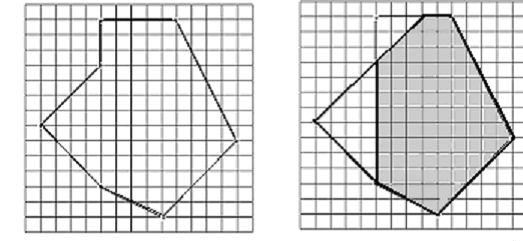
POJ 1279 Art Gallery 半平面交+求多边形核的面积
裸的:半平面交+求多边形核的面积
|
Art Gallery
Description
The art galleries of the new and very futuristic building of the Center for Balkan Cooperation have the form of polygons (not necessarily convex). When a big exhibition is organized, watching over all of the pictures is a big security concern. Your task is that for a given gallery to write a program which finds the surface of the area of the floor, from which each point on the walls of the gallery is visible. On the figure 1. a map of a gallery is given in some co-ordinate system. The area wanted is shaded on the figure 2.
Input
The number of tasks T that your program have to solve will be on the first row of the input file. Input data for each task start with an integer N, 5 <= N <= 1500. Each of the next N rows of the input will contain the co-ordinates of a vertex of the polygon ? two integers that fit in 16-bit integer type, separated by a single space. Following the row with the co-ordinates of the last vertex for the task comes the line with the number of vertices for the next test and so on.
Output
For each test you must write on one line the required surface - a number with exactly two digits after the decimal point (the number should be rounded to the second digit after the decimal point).
Sample Input 1 7 0 0 4 4 4 7 9 7 13 -1 8 -6 4 -4 Sample Output 80.00 Source
Southeastern Europe 2002
|
[Submit] [Go Back] [Status] [Discuss]
/* ***********************************************
Author :CKboss
Created Time :2015年04月09日 星期四 19时43分00秒
File Name :POJ1279.cpp
************************************************ */
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <string>
#include <cmath>
#include <cstdlib>
#include <vector>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define mp make_pair
#define pb push_back
const double eps = 1e-8;
const double pi = acos(-1.0);
const double inf = 1e20;
const int maxp = 2111;
int dcmp(double d) { if(fabs(d)<eps) return 0; return (d<0)?-1:1; }
inline double sqr(double x) { return x*x; }
struct point
{
double x,y;
point(double _x=0,double _y=0):x(_x),y(_y){}
void input() { scanf("%lf%lf",&x,&y); }
void output() { printf("%.2lf %.2lf\n",x,y); }
bool operator==(point a) const { return dcmp(a.x-x)==0&&dcmp(a.y-y)==0; }
bool operator<(point a) const { return dcmp(a.x-x)==0?dcmp(y-a.y)<0:x<a.x; }
double len() { return hypot(x,y); }
double len2() { return x*x+y*y; }
double distance(point p) { return hypot(x-p.x,y-p.y); }
point add(point p) { return point(x+p.x,y+p.y); }
point sub(point p) { return point(x-p.x,y-p.y); }
point mul(double b) { return point(x*b,y*b); }
point div(double b) { return point(x/b,y/b); }
double dot(point p) { return x*p.x+y*p.y; }
double det(point p) { return x*p.y-y*p.x; }
double rad(point a,point b)
{
point p=*this;
return fabs(atan2(fabs(a.sub(p).det(b.sub(p))),a.sub(p).dot(b.sub(p))));
}
};
struct line
{
point a,b;
line(){}
line(point _a,point _b) { a=_a; b=_b; }
bool operator==(const line v) const { return (a==v.a)&&(b==v.b); }
bool parallel(line v) { return dcmp(b.sub(a).det(v.b.sub(v.a)))==0; }
point crosspoint(line v)
{
double a1=v.b.sub(v.a).det(a.sub(v.a));
double a2=v.b.sub(v.a).det(b.sub(v.a));
return point((a.x*a2-b.x*a1)/(a2-a1),(a.y*a2-b.y*a1)/(a2-a1));
}
};
struct polygon
{
int n;
point p[maxp];
line l[maxp];
double getarea()
{
double sum=0;
int i;
for(i=0;i<n;i++)
{
sum+=p[i].det(p[(i+1)%n]);
}
return fabs(sum)/2;
}
};
struct halfplane:public line
{
double angle;
halfplane(){}
/// a-->b left
halfplane(point _a,point _b){ a=_a; b=_b;}
halfplane(line v) { a=v.a; b=v.b; }
void calcangle() { angle=atan2(b.y-a.y,b.x-a.x); }
bool operator<(const halfplane &b) const { return angle<b.angle; }
};
struct halfplanes
{
int n;
halfplane hp[maxp];
point p[maxp];
int que[maxp];
int st,ed;
void push(halfplane tmp)
{
hp[n++]=tmp;
}
void unique()
{
int m=1,i;
for(i=1;i<n;i++)
{
if(dcmp(hp[i].angle-hp[i-1].angle)) hp[m++]=hp[i];
else if(dcmp(hp[m-1].b.sub(hp[m-1].a).det(hp[i].a.sub(hp[m-1].a))>0))
hp[m-1]=hp[i];
}
n=m;
}
bool halfplaneinsert()
{
int i;
for(int i=0;i<n;i++) hp[i].calcangle();
sort(hp,hp+n);
unique();
que[st=0]=0; que[ed=1]=1;
p[1]=hp[0].crosspoint(hp[1]);
for(i=2;i<n;i++)
{
while(st<ed&&dcmp((hp[i].b.sub(hp[i].a).det(p[ed].sub(hp[i].a))))<0) ed--;
while(st<ed&&dcmp((hp[i].b.sub(hp[i].a).det(p[st+1].sub(hp[i].a))))<0) st++;
que[++ed]=i;
if(hp[i].parallel(hp[que[ed-1]])) return false;
p[ed]=hp[i].crosspoint(hp[que[ed-1]]);
}
while(st<ed&&dcmp((hp[st].b.sub(hp[que[st]].a).det(p[ed].sub(hp[que[st]].a))))<0) ed--;
while(st<ed&&dcmp((hp[que[ed]].b.sub(hp[que[ed]].a).det(p[st+1].sub(hp[que[ed]].a))))<0) st++;
if(st+1>=ed) return false;
return true;
}
void getconvex(polygon &con)
{
p[st]=hp[que[st]].crosspoint(hp[que[ed]]);
con.n=ed-st+1;
int j=st,i=0;
for(;j<=ed;i++,j++) con.p[i]=p[j];
}
};
int main()
{
//freopen("in.txt","r",stdin);
//freopen("out.txt","w",stdout);
int T_T;
scanf("%d",&T_T);
while(T_T--)
{
int n;
scanf("%d",&n);
vector<point> vp;
for(int i=0;i<n;i++)
{
point tp; tp.input(); vp.pb(tp);
}
halfplanes hfs; hfs.n=0;
for(int i=0;i<n;i++)
{
//// p[i] <--- p[i+1]
hfs.push(halfplane(vp[(i+1)%n],vp[i]));
}
hfs.halfplaneinsert();
polygon pol;
hfs.getconvex(pol);
double area=pol.getarea();
printf("%.2lf\n",area);
}
return 0;
}