Trie树:应用于统计和排序
说明:本文转自 http://blog.csdn.net/hguisu/article/details/8131559
1. 什么是trie树
1.Trie树 (特例结构树)
2. 三个基本特性:
3 .例子
和二叉查找树不同,在trie树中,每个结点上并非存储一个元素。trie树把要查找的关键词看作一个字符序列。并根据构成关键词字符的先后顺序构造用于检索的树结构。
在trie树上进行检索类似于查阅英语词典。
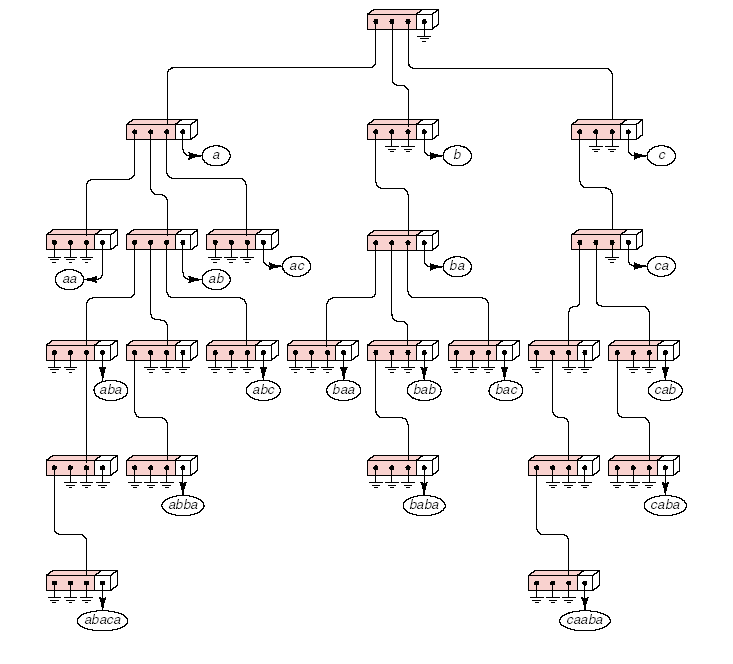
例如,电子英文词典,为了方便用户快速检索英语单词,可以建立一棵trie树。例如词典由下面的单词成:a、b、c、aa、ab、ac、ba、ca、aba、abc、baa、bab、bac、cab、abba、baba、caba、abaca、caaba
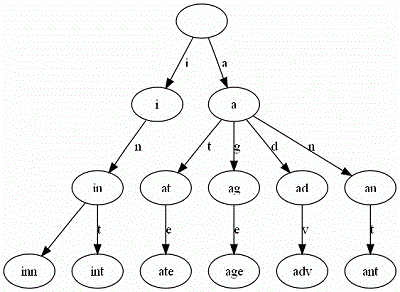
再举一个例子。给出一组单词,inn, int, at, age, adv, ant, 我们可以得到下面的Trie:
可以看出:
- 每条边对应一个字母。
- 每个节点对应一项前缀。叶节点对应最长前缀,即单词本身。
- 单词inn与单词int有共同的前缀“in”, 因此他们共享左边的一条分支,root->i->in。同理,ate, age, adv, 和ant共享前缀"a",所以他们共享从根节点到节点"a"的边。
查询操纵非常简单。比如要查找int,顺着路径i -> in -> int就找到了。
2. trie树的实现
1.插入过程
对于一个单词,从根开始,沿着单词的各个字母所对应的树中的节点分支向下走,直到单词遍历完,将最后的节点标记为红色,表示该单词已插入trie树。
2. 查找过程
其方法为:
(1) 从根结点开始一次搜索;
(2) 取得要查找关键词的第一个字母,并根据该字母选择对应的子树并转到该子树继续进行检索;
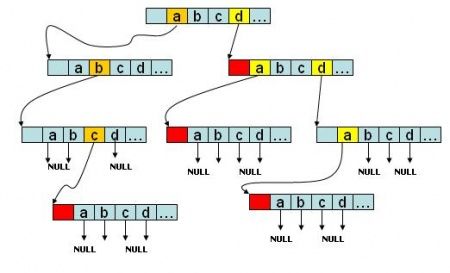
即从根开始按照单词的字母顺序向下遍历trie树,一旦发现某个节点标记不存在或者单词遍历完成而最后的节点未标记为红色,则表示该单词不存在,若最后的节点标记为红色,表示该单词存在。如下图中:trie树中存在的就是abc、d、da、dda四个单词。在实际的问题中可以将标记颜色的标志位改为数量count等其他符合题目要求的变量。
- // stdafx.h : include file for standard system include files,
- // or project specific include files that are used frequently, but
- // are changed infrequently
- //
- #pragma once
- #include <stdio.h>
- #include "stdlib.h"
- #include <iostream>
- #include <string.h>
- using namespace std;
- //宏定义
- #define TRUE 1
- #define FALSE 0
- #define NULL 0
- #define OK 1
- #define ERROR 0
- #define INFEASIBLE -1
- #define OVERFLOW -2
- const int num_chars = 26;
- class Trie {
- public:
- Trie();
- Trie(Trie& tr);
- virtual ~Trie();
- int trie_search(const char* word, char* entry ) const;
- int insert(const char* word, const char* entry);
- int remove(const char* word, char* entry);
- protected:
- struct Trie_node{
- char* data; //若不为空,表示从root到此结点构成一个单词
- Trie_node* branch[num_chars]; //分支
- Trie_node(); //构造函数
- };
- Trie_node* root; //根结点(指针)
- };
- // Test.cpp : Defines the entry point for the console application.
- //
- #include "stdafx.h"
- Trie::Trie_node::Trie_node() {
- data = NULL;
- for (int i=0; i<num_chars; ++i)
- branch[i] = NULL;
- }
- Trie::Trie():root(NULL) {}
- Trie::~Trie(){}
- int Trie::trie_search(const char* word, char* entry ) const {
- int position = 0; //层数
- char char_code;
- Trie_node *location = root; //从根结点开始
- while( location!=NULL && *word!=0 ) {
- if (*word >= 'A' && *word <= 'Z')
- char_code = *word-'A';
- else if (*word>='a' && *word<='z')
- char_code = *word-'a';
- else return 0;// 不合法的单词
- //转入相应分支指针
- location = location->branch[char_code];
- position++;
- word++;
- }
- //找到,获取数据,成功返回
- if ( location != NULL && location->data != NULL ) {
- strcpy(entry,location->data);
- return 1;
- }
- else return 0;// 不合法的单词
- }
- int Trie::insert(const char* word, const char* entry) {
- int result = 1, position = 0;
- if ( root == NULL ) root = new Trie_node; //初始插入,根结点为空
- char char_code;
- Trie_node *location = root; //从根结点开始
- while( location!=NULL && *word!=0 ) {
- if (*word>='A' && *word<='Z') char_code = *word-'A';
- else if (*word>='a' && *word<='z') char_code = *word-'a';
- else return 0;// 不合法的单词
- //不存在此分支
- if( location->branch[char_code] == NULL )
- location->branch[char_code] = new Trie_node; //创建空分支
- //转入分支
- location = location->branch[char_code];
- position++;word++; }
- if (location->data != NULL) result = 0;//欲插入的单词已经存在
- else { //插入数据
- location->data = new char[strlen(entry)+1]; //分配内存
- strcpy(location->data, entry); //给data赋值表明单词存在
- }
- return result;
- }
- int main(){
- Trie t;
- char entry[100];
- t.insert("a", "DET");
- t.insert("abacus","NOUN");
- t.insert("abalone","NOUN");
- t.insert("abandon","VERB");
- t.insert("abandoned","ADJ");
- t.insert("abashed","ADJ");
- t.insert("abate","VERB");
- t.insert("this", "PRON");
- if (t.trie_search("this", entry))
- cout<<"'this' was found. pos: "<<entry<<endl;
- if (t.trie_search("abate", entry))
- cout<<"'abate' is found. pos: "<<entry<<endl;
- if (t.trie_search("baby", entry))
- cout<<"'baby' is found. pos: "<<entry<<endl;
- else
- cout<<"'baby' does not exist at all!"<<endl;
- }
3. 查找分析
若关键字长度最大是5,则利用trie树,利用5次比较可以从26^5=11881376个可能的关键字中检索出指定的关键字。而利用二叉查找树至少要进行
3. trie树的应用:
1. 字符串检索,词频统计,搜索引擎的热门查询
事先将已知的一些字符串(字典)的有关信息保存到trie树里,查找另外一些未知字符串是否出现过或者出现频率。
举例:
1)有一个1G大小的一个文件,里面每一行是一个词,词的大小不超过16字节,内存限制大小是1M。返回频数最高的100个词。
2)给出N 个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
3)给出一个词典,其中的单词为不良单词。单词均为小写字母。再给出一段文本,文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如,若rob是不良单词,那么文本problem含有不良单词。
4)1000万字符串,其中有些是重复的,需要把重复的全部去掉,保留没有重复的字符串
5)寻找热门查询:搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来,每个查询串的长度为1-255字节。假设目前有一千万个记录,这些查询串的重复读比较高,虽然总数是1千万,但是如果去除重复和,不超过3百万个。一个查询串的重复度越高,说明查询它的用户越多,也就越热门。请你统计最热门的10个查询串,要求使用的内存不能超过1G。
2. 字符串最长公共前缀
Trie树利用多个字符串的公共前缀来节省存储空间,反之,当我们把大量字符串存储到一棵trie树上时,我们可以快速得到某些字符串的公共前缀。举例:
1) 给出N 个小写英文字母串,以及Q 个询问,即询问某两个串的最长公共前缀的长度是多少. 解决方案:
首先对所有的串建立其对应的字母树。此时发现,对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数,于是,问题就转化为了离线 (Offline)的最近公共祖先(Least Common Ancestor,简称LCA)问题。
而最近公共祖先问题同样是一个经典问题,可以用下面几种方法:
1. 利用并查集(Disjoint Set),可以采用采用经典的Tarjan 算法;
2. 求出字母树的欧拉序列(Euler Sequence )后,就可以转为经典的最小值查询(Range Minimum Query,简称RMQ)问题了;
3. 排序
Trie树是一棵多叉树,只要先序遍历整棵树,输出相应的字符串便是按字典序排序的结果。
举例: 给你N 个互不相同的仅由一个单词构成的英文名,让你将它们按字典序从小到大排序输出。
4 作为其他数据结构和算法的辅助结构
如后缀树,AC自动机等。