眼科病床的合理安排
(陈旭东、戴珍团、陈广臻)
摘要
本文通过建立一个病人入住策略来改变医院“拥堵”的情况,达到整体上节约病人的看病时间,从而在一定程度上解决“看病难”的问题。
针对在“FCFS”策略下导致等待入院队伍“拥塞”问题,我们借鉴计算机操作系统中的“高优先权优先调度、非抢占式时间片轮转”的思想,提出了非抢占式优先权优先排队模型。
非抢占式优先权优先排队模型通过动态改变排队成员入院优先级的模型,这种模型照顾了入院到住院周期较短的患者,使之可以在进入系统后便可以获得优先处理,引入了最高优先权优先调度算法。
最终通过计算机模拟实验得到了能在11-13天内有效的缓解等待队伍过长问题的手术安排方案。
通过对历史数据的分析统计可以得到不同疾病的病人在不同时间入住产生的平均占用病床的时间。从而给不同的疾病在不同的时点入住给予不同的优先权,对于同一种疾病则还是按照先到先服务的策略安排病人入住。对于这样的一个策略,其目标是使得病人平均占用床的时间最小。这也与评价指标体系以一个标准手术准备时间去衡量不同入住策略的优劣相吻合。
根据住院部目前的情况安排第二天的入住情况则只需根据目前的排队等待入住队伍应用优先权就可以大致确定第二天入住的病人情况。对于第三问可以根据第二问的预测情况和第二天新就诊的病人加入的排队队伍作为当前情况来决定第三天的入住情况,同样的方法可以确定未来的病人入住情况。所以是可以模拟出这样的一个过程来预测病人的入住时间,在这个过程中主要对病人的日就诊人数和日出院人数的分布做一个估计,本文的估计结果是日就诊人数服从泊松而日出院人数服从正态分布。问题四的情况相比与问题二的模型增加了在星期六、星期日不上班的约束条件而目标并没有改变。于是对问题二的约束条件做了相应的调整得到了相应的结果。问题五从管理者的角度出发,要求将病床按不同的疾病在满足病人总逗留时间最短的目标将病床分配。于是对这个问题和做法是针对不同的病症对数据做了相应的检验,可以认为该模型是满足多服务台排队系统的。
最终将各病症分成5个系统,再按照多服务台系统的平均逗留时间计算公式计算平均逗留时间。以各病症分配的床位数为变量,求最小的总平均逗留时间,得到最优解分配量。
关键字: 优先权 操作系统 排队论 计算机模拟调度算法
一、问题重述
我国的医疗体制改革问题一直是大家所关心的民生问题,本次赛题关于眼科病床的合理安排,主要问题有以下,对于目前的病床确定的情况下,考虑到不同时期病人数会有所不同所以排队的情况是难以避免。但是本题例子中的住院部对此采取的方法是先到先服务(FCFS)的相对公平策略来处理。由于先到先服务没有考虑到不同病症之间对手术准备及手术后观察期的不同使等待住院的病人不断增加。为了改变这种状况,要求分析以往的数据确定一个合理的评价病床安排模型优劣的评价指标体系。还要跟据住院部目前的情况,建立合理的病床安排模型,再应用这个模型及目前的病人数及排队中的病人来安排第二天入住的病人,最后再用第一问中的评价指标体系来对这个病床安排模型做出评价。
问题三,站在病人的角度出发,在门诊的时候了解了病人的症状之后,通过建立模型,利用目前的入住情况和等待入住的病人排队情况,预测病人需等待多长时间才能够入住。
问题四,则从医生的角度来看,目前的一周双修工作制度同样适合医生的话。在周六、周日医生不上班的情况下,我们是否应该考虑改变模型,或重新建立模型。这里的模型就是指病人的入住策略。
问题五,从医院的管理角度提出建议,为方便医院对医疗设备的管理。对病床进行分类,在使病人在服务系统内平均逗留时间最短条件下确定各症状的病床数
二、问题的分析
分析医院当前数据可以知道“等待住院病人队列却越来越长”这种现象主要是由于“FCFS规则安排住院”引起的,对于本题中的关键问题在于确定一个合适的入住方案来决定病人的入住情况,再分析这样的方案是否能满足我们的模型评价指标体系:
1.某些白内障病人的住院时间过长。例如25,30,32号病人从星期一开始住院,直到下星期一才能正式开始做手术,住院时间为12天;20号病人从星期日开始住院,到第2天即可做手术,住院周期为6天,比第一种情况少了6天。这时可以采用“高优先权优先调度、非抢占式时间片轮转”[1]的思想,进一步修正“FCFS”策略来缓解这类长期无效占用病床的情况,通过计算每种病在当天的优先权,按优先级重新对队伍排序,之后当出现有空闲病床的情况时,安排优先级最高的病人入住(例如将正在排队的白内障(双眼)病人通过合理的权重系数矩阵尽可能使得在星期日、星期六的时候获到较高的优先级,而在星期一、星期二、星期三的时候优先级最低)。
2.对于问题一,我们可以通过病床周转次数、病人门诊到入院时间、入院到手术时间、住院周期这些指标评价模型优劣。
问题二,也就是需要解决“FCFS规则安排住院”所引起的问题---住院时间过长。通过该原因分析可知只需在“FCFS”策略中引入“高优先权优先住院”策略即可得到第二天各个病人的入住顺序。最后判断队长则可以知道该方法是否合理,然后通过计算这些指标来分析该模型优劣。
问题三:先利用问题二中的模型求解当前情况下这位病人第2天是否可能入住,如果不可入住将该病人加入排队队列->重新计算第3天是否可能入住…,不断重复的迭代即可得到判断该病人大致的入住区间。
问题四:这个问题基本可以采用问题二中的高优先权优先模型解决,但是在这个问题中由于白内障病患只能在星期一、星期三做手术,故问题二和问题四中的这种情况是一样的,外伤在问题四和问题二中的权重值也一样的。只要确定了问题四青光眼和视网膜疾病在星期六、星期天不做手术的情况下的权重变化关系,即可利用模型二求解结果。
问题五:第五问是一个最优比例分配问题,我们的目标函数是病人在系统内总的逗留时间最短。我们通过假设和一些统计检验,确定可以用多台服务系统模型来处理这个问题,而多台服务系统的平均逗留时间函数是可知,从而我们的目标函数也就给出。对于约束条件和前面的一样。
三、模型的假设及说明
1.单位时间内患者到门诊的总人数服从泊松分布,每天各种病症到诊数也是服从泊松分布。
2.假设白内障(单眼)和白内障(双眼)是不同的病。因为白内障中的单眼病人和双眼病人是有各自的限制条件,白内障(单眼)病人只能在星期一或星期三做手术,而白内障(双眼)只能在星期一和星期三手术,所以将这两种情况作为单独的两种情况考虑;
3.病人占用病床的时间服从负指数分布;
4.不考虑非外伤疾病的急诊情况;
5.同一种病按先到先服务的策略;
四、符号说明
| A(i,j) |
第i类病在星期j下的权重系数,i=1..5,j=1..7 |
| B(i) |
当前第i类病症的等待队长,i=1..5 |
|
|
第n天的空闲床位数量,n>=1(从2008/09/10开始计数) |
|
|
指等待住院病人的排队优先顺序,数值大者优先住院 |
|
|
等待住院的白内障病人的优先权(单眼) |
|
|
等待住院的白内障病人的优先权(双眼) |
|
|
等待住院的青光眼病人的优先权 |
|
|
等待住院的视网膜疾病病人的优先权 |
|
|
等待住院的外伤病人的优先权 |
| Z(i,:) |
表示一个矩阵的第i行数据(Z为任意矩阵) |
| Z(:,j) |
表示一个矩阵的第j列数据(Z为任意矩阵) |
五、模型的建立及求解
(一)问题一:评价指标体系
1.面向医院
医院中,在康复期相对确定的情况下,从统计数据我们可以发现,制约病床周转的主要因素在于实际术前准备期超过了理想情况下的准备期。对此,由统计数据,我们假定各个准备期的均值近似为这种病理想情况下的准备期。因此,可以把实际术前准备与理想情况下的准备期的相对误差的平均值作为衡量安排模型的重要因素。
其中,![]() 为平均准备期相对误差,
为平均准备期相对误差,![]() 表示为从i病人从入院到做手术的时间,
表示为从i病人从入院到做手术的时间,![]() 表示第j种病的病人在理想状态下的准备期时间,其值近似为下表相应病种的均值。
表示第j种病的病人在理想状态下的准备期时间,其值近似为下表相应病种的均值。
| 白内障 |
白内障(双眼) |
外伤 |
视网膜疾病 |
青光眼 |
|
| 一天准备期 |
23 |
12 |
55 |
0 |
0 |
| 二天准备期 |
22 |
21 |
0 |
63 |
23 |
| 三天准备期 |
0 |
0 |
0 |
38 |
16 |
| 均值 |
1.488889 |
1.636364 |
1 |
2.376238 |
2.410256 |
| 理想状态值 |
1.488889 |
1.636364 |
1 |
2.376238 |
2.410256 |
(表一 各种病的理想状态康复时间)
2.面向患者
对于每个患者而言,都希望自己从门诊到住院、手术的时间最短。但作为医院而言,则总是希望能使平均周转时间最短。这不仅会有效地提高医院资源的利用率,而且可以使大多数患者感到满意。对此,把平均周转时间描述为:
患者平均周转时间与平均患者从门诊到手术的时间![]() 之比,即W=T/
之比,即W=T/![]() ,称为带权周转时间,它可以表示为:
,称为带权周转时间,它可以表示为:
其中,带权周转时间越大,当![]() 已知情况下,患者从门诊到手术的时间越小。对于患者越有利。
已知情况下,患者从门诊到手术的时间越小。对于患者越有利。
总之,要评定病床安排模型优劣,我们首先计算![]() 与W,如果
与W,如果![]() 越小,且W越大该安排模型越好。要评定病床安排模型优劣,我们首先计算
越小,且W越大该安排模型越好。要评定病床安排模型优劣,我们首先计算![]() 与W,如果
与W,如果![]() 越大,且W越小该安排模型越不好。
越大,且W越小该安排模型越不好。
(二)问题二:非抢占式优先权优先排队模型
模型说明:由于原来的对所有的非急诊的评价采用先到先服务的策略造成了队列越来越长的问题,我们的改进策略是相当于对就诊了的病人分排五个队列,对每个队列在不同的时间有不同的优先权,每当空出一个病床则比较各队的排在第一位置的病人。如果谁的优先权大则安排谁入住。
图5-2-1 高优先权优先排队模型流程图
我们提出了高优先权优先的排队模型[1]:各种病症中排于第一位的病人![]() 病人的优先权计算公式如下:
病人的优先权计算公式如下:
![]() ,
,
其中![]() 为加权系数.
为加权系数. ![]() 为排队队伍中的患者已等待时间天数,k为常数,这里取0.1。这里引入B是为了防止个别队伍排队过长,而引入患者的等待天数则是为了计算病人排队的时间价值(FCFS)。
为排队队伍中的患者已等待时间天数,k为常数,这里取0.1。这里引入B是为了防止个别队伍排队过长,而引入患者的等待天数则是为了计算病人排队的时间价值(FCFS)。
假设在目前时刻等待住院的病人队长为n,
如果要保证住院到手术时间最短,可通过5种病在星期时间下的入住优先权矩阵A:
矩阵A的行分别指白内障(单眼)、白内障(双眼)、青光眼、视网膜疾病、外伤类型,矩阵B的列分别指星期一到星期日。
以第5行数据为例,可以从该行数据中看出外伤患者无论在何时,外伤患者的优先级别都是最高的。以第1列数据为例,优先级别关系为:外伤>白内障(单眼)> (青光眼=视网膜疾病)> 白内障(双眼),青光眼和视网膜疾病之间按“FCFS”策略排队。
然后再取
![]() ’,
’,
![]() ,这里我们取
,这里我们取![]()
这时当病房中有n位病人要出院时,我们可以认为是一位一位病人出院,则每次计算各队中排在第一位的病人的优先权,这样迭代n次则可以将这n个出院的空位填满。可以实时检测患者等待队列(设队长为m)中是否有患者;如果存在则通过以上的优先权计算确定5种病的优先级别,然后根据此优先级别对所有患者进行排序并放入已排序等待队列中;这时服务台从中选取min(n,m)个患者安排住院,这样的策略可以满足必要手术准备时间的情况下住院到手术时间最短,解决排队队长过长的问题;
模型求解过程
Step 1 确定初始时间值
在2008年09月10日为初始时间值,并且以后所有数据的计算都从该时刻开始,记为T;
Step 2 用题目所给的数据计算出各病种的比例情况
![]() ,
,
其中![]() 为别对应白内障(单眼)、白内障(双眼)、青光眼、视网膜疾病、外伤的分布比例;
为别对应白内障(单眼)、白内障(双眼)、青光眼、视网膜疾病、外伤的分布比例;
Step 3 计算每类病人何时出院
由于题中对于星期时间的手术安排限制和手术准备时间的要求,于是不同的病症在不同的入住时点有所不同,通过对历史数据的统计分析得到不同症状的病人在不同的时点入住的平均出院的时间,
![]() ;
;
其中![]() 表示距离初始时间值t天的出院人数,
表示距离初始时间值t天的出院人数,
对于2008年9月11日之后的数据,都需要通过计算距离出院时间间隔,
距离出院时间间隔i=病人出院时间预测值-初始时间值
最后,d(i)=d(i)+1,
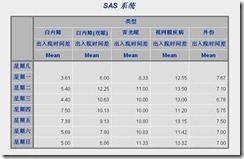
这里的病人出入院时间平均值可以利用SAS分析原始数据得到,具体结果如下图
图5-2-2
Step 4 计算各病种的门诊人数
对题目数据中的门诊时间做统计分析可得![]() ,
,
其中H(1,:)为t=1的各病种门诊人数,H(2,:)为T的各病种门诊人数;H(:,1),H(:,2),H(:,3),H(:,4),H(:,5)分别为白内障(单眼)、白内障(双眼)、青光眼、视网膜疾病、外伤对应时间的人数
我们假设每日到门诊就诊的人数是服从Poisson分布的,同时我们对题目所给的数据做关于每日就诊人数的Poisson分布的非参数检验,检验结果如下图:从下图的结果表可知Poisson分布的均值为8.6885,数据的真实值与理论值的差分别为最大绝对值为0.044,正值为0.044,负值为-0.029.检验的K-S统计量Z=0.342,双侧检验的近似概率为1,因为![]() ,所以接受原假设认为日就诊量是服从Poisson分布的。
,所以接受原假设认为日就诊量是服从Poisson分布的。
图5-2-3
在确定了日就诊量的分布规律之后,医院的队长和系统平稳后的平均等待时间等都可以通过Possion分布预测进入数值仿真。
Step 5 计算当前每种病的等待住院人数:
![]() 表示当前的住院等待人数,D为当前门诊人数,k为对应病种的占有比例
表示当前的住院等待人数,D为当前门诊人数,k为对应病种的占有比例
Step 6 通过优先权值计算公式计算5种病情的优先权
Step 7 根据优先权对所有数据进行排序
Step 8判断是否有空闲床位数,如有则安排入院(安排步骤7中排名靠前的病人住院)。反之,则执行9
9.退出
通过这个算法可以解得如下结果:
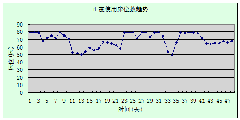
图5-2-4 等待住院人数变化趋势
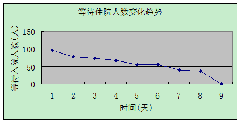
图5-2-5 正在使用床位数趋势
结果分析:
从图5-2-4和图5-2-5中可以得出:
1.t=1,2,3的时候正在使用床位数处于饱和状态时,等待住院人数上升,这正好符合实际;因为当时没有人出院,而每天都会有一定的病人来门诊,故在刚开始排队的时段内等待住院人数将会上升。
2.当正在使用床位数长期未达到饱和的时候,这时候说明这期间住院人数大于出院人数,故等待住院人数呈下降趋势,图5-2-4和图5-2-5正好就反映了这一点。
3.从t=15开始,图5-2-5有时候仍能使正在床位数达到饱和状态(如t=23-25期间),这说明采用该模型的策略安排住院病人能够比较有效的处理“等待住院病人队列却越来越长”问题。
(三)问题三
从病人的角度出发,对于自己目前在队伍中所处理的位置可以从目前的队长情况确定,自己将于何时入住,这个问题是问题二的外推。问题二解决了第二天哪些病人可以入住的情况,同样我们可以往下推得知第三天、第四天有哪些病人可以入住。队伍的情况也随着时间的推移在变动。从而一个病人在队伍中的位置也在变动,同样他所处的时间点也在变化,于是它的优先权也在变化。这样一个动态过程实现了病人的入住,所以我们可要模拟这个过程就可以大致知道病人可以在何时入住。我们的分析以当前数据为依据,在问题二中所得到的优先权矩阵的基础上处理问题三。
(四)问题四
问题四与问题二之间有一些相同之处:
1.白内障(双眼)和白内障病人的安排方案仍然不变,对于白内障(双眼)的患者只要尽可能的在星期六或星期天住院,那么星期一的时候就能立刻做手术了,同理,对于白内障患者与问题二安排也相同;按照题目要求,这种病人是只能在星期一或星期三才能手术,所以在星期六或星期日也是不可能做白内障手术的。
2.外伤患者的手术安排:只要外伤患者出现就安排住院,第二天就做手术了,所以在入住优先权重矩阵中第5行的权重数据对于问题二和问题四也是相同的,故此病种不会对问题二的方案结果影响太大。
问题四和问题二中对青光眼和视网膜疾病患者的安排是不同的,因为这2种疾病都没有特殊要求,在星期六、星期日中的为这2种患者做手术的情况也是相同的,所以如果星期六和星期天不安排手术,那么需要将问题二中这2种病在星期二、星期三、星期四的权重转移。
故可调整5种病在星期时间下的入住优先权矩阵A’为:
这时,只需令模型二中的入住优先权矩阵A=A’,
通过求解可得结果:
图4-1-1等待住院人数变化趋势
图4-1-2正在使用床位数趋势
(五)问题五
设![]() 为第i种症状的病床数,且满足
为第i种症状的病床数,且满足![]() 。由于各种病床区分开来,各种病又相互独立,所以对各种病症来说都是一个多服务台的排队系统。对于多服务台排队系统而言主要有两个假设:
。由于各种病床区分开来,各种病又相互独立,所以对各种病症来说都是一个多服务台的排队系统。对于多服务台排队系统而言主要有两个假设:
1、顾客的到来服从参数为![]() 泊松分布(到来时间间隔服从负指数分布)
泊松分布(到来时间间隔服从负指数分布)
2、服务台相互独立,服务的时间服从参数为![]() 负指数分布,对各系统分析如下,对各病症病人的门诊量的Poisson分布检验如下,从下表可知各分量服从Poisson分布且泊松分布的均值分别为1.923、2。4182、1.5366、2.8814、1.600。
负指数分布,对各系统分析如下,对各病症病人的门诊量的Poisson分布检验如下,从下表可知各分量服从Poisson分布且泊松分布的均值分别为1.923、2。4182、1.5366、2.8814、1.600。
对于![]() 系统有平均逗留时间为
系统有平均逗留时间为![]()
从以上的各病症的平均逗留时间我们将不同的病症所需的平均逗留时间求和,使得所有病人在系统内的平均逗留时间(含等待入院及住院时间)最短的病床比例分配模型。我们的目标就是对各病症的平均逗留时间做求和取最小值。于是所建立一个优化模型可以用Lingo软件求解,得如下结果:
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
目标值为137.8。
六、模型的评价
通过计算机模拟,成功地改变了医院现阶段入院病人堵塞的问题。考虑不同时间对入院的影响,在不同的工作日对于不同的患者有不同的优先关系,改变了以前排队的顺序。但由于其优先顺序的权值很难给定最优解。
参考文献:
[1] 汤小丹;梁红兵;哲凤屏;汤子瀛,《计算机操作系统(第三版)》,西安:西安电子科技大学出版社,2007年,起止页码:85-113。
[2] 刁在筠 刘桂真 宿 洁 马建华《运筹学(第三版)》,高等教育出版社 2007年,起止页码:270-273。