一小时了解数据挖掘③:详解大数据挖掘的分类技术
数据挖掘分类技术
从分类问题的提出至今,已经衍生出了很多具体的分类技术。下面主要简单介绍四种最常用的分类技术,不过因为原理和具体的算法实现及优化不是本书的重点,所以我们尽量用应用人员能够理解的语言来表述这些技术。
在我们学习这些算法之前必须要清楚一点,分类算法不会百分百准确。每个算法在测试集上的运行都会有一个准确率的指标。用不同的算法做成的分类器(Classifier)在不同的数据集上也会有不同的表现。
KNN,K最近邻算法
K最近邻(K-Nearest Neighbor,KNN)分类算法可以说是整个数据挖掘分类技术中最简单的方法。所谓K最近邻,就是K个最近的邻居,说的是每个样本都可以用它最接近的K个邻居来代表。
我们用一个简单的例子来说明KNN算法的概念。如果您住在一个市中心的住宅内,周围若干个小区的同类大小房子售价都在280万到300万之间,那么我们可以把你的房子和它的近邻们归类到一起,估计也可以售280万到300万之间。同样,您的朋友住在郊区,他周围的同类房子售价都在110万到120万之间,那么他的房子和近邻的同类房子归类之后,售价也在110 万到120万之间。
KNN算法的核心思想是如果一个样本在特征空间中的K个最相似的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。
KNN方法在类别决策时,只与极少量的相邻样本有关。由于KNN方法主要靠周围有限的邻近样本,而不是靠判别类域的方法来确定所属类别,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合。
决策树(Decision Tree)
如果说KNN是最简单的方法,那决策树应该是最直观最容易理解的分类算法。最简单的决策树的形式是If-Then(如果-就)式的决策方式的树形分叉。比如下面这样一棵决策树,根据样本的相貌和财富两个属性把所有样本分成“高富帅”、“帅哥”、“高富”和“屌丝”四类。
决策树上的每个节点要么是一个新的决策节点,要么就是一个代表分类的叶子,而每一个分支则代表一个测试的输出。决策节点上做的是对属性的判断,而所有的叶子节点就是一个类别。决策树要解决的问题就是用哪些属性充当这棵树的各个节点的问题,而其中最关键的是根节点(Root Node),在它的上面没有其他节点,其他所有的属性都是它的后续节点。在上面的例子中,(obj.相貌==“帅”)就是根节点,两个(obj.财富>=1000000000)是根节点下一层的两个决策节点,四个print标志着四个叶子节点,各自对应一个类别。
所有的对象在进入决策树之后根据各自的“相貌”和“财富”属性都会被归到四个分类中的某一类。
大多数分类算法(如下面要提的神经网络、支持向量机等)都是一种类似于黑盒子式的输出结果,你无法搞清楚具体的分类方式,而决策树让人一目了然,十分方便。决策树按分裂准则的不同可分为基于信息论的方法和最小GINI指标 (Gini Index)方法等。
神经网络(Neural Net)
在KNN算法和决策树算法之后,我们来看一下神经网络。神经网络就像是一个爱学习的孩子,你教他的知识他不会忘记,而且会学以致用。我们把学习集(Learning Set)中的每个输入加到神经网络中,并告诉神经网络输出应该是什么分类。在全部学习集都运行完成之后,神经网络就根据这些例子总结出他自己的想法,到底他是怎么归纳的就是一个黑盒了。之后我们就可以把测试集(Testing Set)中的测试例子用神经网络来分别作测试,如果测试通过(比如80%或90%的正确率),那么神经网络就构建成功了。我们之后就可以用这个神经网络来判断事务的分类。
神经网络是通过对人脑的基本单元——神经元的建模和连接,探索模拟人脑神经系统功能的模型,并研制一种具有学习、联想、记忆和模式识别等智能信息处理功能的人工系统。神经网络的一个重要特性是它能够从环境中学习,并把学习的结果分别存储于网络的突触连接中。神经网络的学习是一个过程,在其所处环境的激励下,相继给网络输入一些样本模式,并按照一定的规则(学习算法)调整网络各层的权值矩阵,待网络各层权值都收敛到一定值,学习过程结束。然后我们就可以用生成的神经网络来对真实数据做分类。
支持向量机SVM(Support Vector Machine)
和上面三种算法相比,支持向量机的说法可能会有一些抽象。我们可以这样理解,尽量把样本中的从更高的维度看起来在一起的样本合在一起,比如在一维(直线)空间里的样本从二维平面上可以把它们分成不同类别,而在二维平面上分散的样本如果我们从第三维空间上来看就可以对它们做分类。支持向量机算法的目的是找到一个最优超平面,使分类间隔最大。最优超平面就是要求分类面不但能将两类正确分开,而且使分类间隔最大。在两类样本中离分类面最近且位于平行于最优超平面的超平面上的点就是支持向量,为找到最优超平面,只要找到所有的支持向量即可。对于非线性支持向量机,通常做法是把线性不可分转化成线性可分,通过一个非线性映射将低维输入空间中的数据特征映射到高维线性特征空间中,在高维空间中求线性最优分类超平面。
支持向量机算法是我们在做数据挖掘应用时很看重的一个算法,而原因是该算法自问世以来就被认为是效果最好的分类算法之一。
分类算法的评估
在整个分类数据挖掘工作的最后阶段,分类器(Classifier)的效果评价所占据的地位不容小视,正如前文所述,没有任何分类器能够百分百的正确,任何分类算法都会发生一定的误差,而在大数据的情况下,有些数据的分类本身就是比较模糊的。因此在实际应用之前对分类器的效果进行评估显得很重要。
对分类器的效果评价方法有很多,由于图形化的展示方式更能为大家所接受,这里介绍两种最常用的方式,ROC曲线和Lift曲线来做分类器的评估。
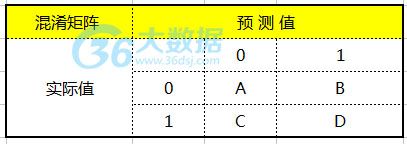
在介绍两种曲线之前,为了方便说明,假设一个用于二分类的分类器最终得出的结果如表所示。
这张表通常被称为混淆矩阵(Confusion Matrix)。在实际应用中,常常把二分类中的具体类别用0和1表示,其中1又常常代表我们关注的类别,比如直邮营销中的最终消费客户可以设定为1,没有转化成功的客户设为0。通信行业客户流失模型中的流失客户可设置为1,没有流失的客户设置为0。矩阵中的各个数字的具体含义为,A表示实际是0预测也是0的个数,B表示实际是0却预测成1的个数,C表示实际是1预测是0的个数,D表示实际是1预测也是1的个数。
下图是一张ROC曲线图,ROC曲线(Receiver Operating Characteristic Curve)是受试者工作特征曲线的缩写,该曲线常用于医疗临床诊断,数据挖掘兴起后也被用于分类器的效果评价。
如上图所示为一张很典型的ROC曲线图,从图中可以看出该曲线的横轴是FPR(False Positive Rate), 纵 轴是 TPR(True Positive Rate)。首先解释一下这两个指标的含义:TPR指的是实际为1预测也是1的概率,也就是混淆矩阵的D/(C+D),即正类(1)的查全率。FPR指的是实际为0预测为1的概率即B/(A+B)。
前面说过,分类中比较关心的都是正类的预测情况,而且分类结果常常是以概率的形式出现的,设定一个阈值,如果概率大于这个阈值那么结果就会是1。而ROC曲线的绘制过程就是根据这个阈值的变化而来的,当阈值为0时,所有的分类结果都是1,此时混淆矩阵中的C和A是0,那 么TPR=1,而FPR也是1,这样曲线达到终点。随着阈值的不断增大,被预测为1的个数会减少,TPR和FPR同时减少,当阈值增大到1时,没有样本被预测为1,此时TPR和FPR都为0。由此可知,TPR和FPR是
同方向变化的,这点在上图中可以得到体现。
由于我们常常要求一个分类器的TPR尽量高,FPR尽量小,表现在图中就是曲线离纵轴越近,预测效果就越好。为了更具体化,人们也通过计算AUC(ROC曲线下方的面积)来评判分类器效果,一般AUC超过0.7就说明分类器有一定效果。在上图中的ROC曲线中,曲线下方的面积AUC数值超过了0.7,所以分类器是有一定效果的。
下面我们再来看Lift曲线的绘制。Lift曲线的绘制方法与ROC曲线是一样的,不同的是Lift曲线考虑的是分类器的准确性,也就是使用分类器获得的正类数量和不使用分类器随机获取正类数量的比例。以直邮营销为例,分类器的好坏就在于与直接随机抽取邮寄相比,采用分类器的结果会给公司带来多少响应客户(即产生多少最终消费),所以Lift分类器在直邮营销领域的应用是相对比较广泛的。
由下图可以发现,Lift曲线的纵轴是Lift值,它的计算公式是![]() ,其中
,其中
![]() ,这个参数的含义是如果采用了分类器,正类的识别比例;而
,这个参数的含义是如果采用了分类器,正类的识别比例;而
![]()
,表示如果不用分类器,用随机的方式抽取出正类的比例。这二者相比自然就解决了如果使用者用分类器分类会使得正类产生的比例会增加多少的问题。Lift曲线的横轴RPP(正类预测比例,Rate of Positive Predictions)的计算公式是![]()
Lift曲线的绘制过程与ROC曲线类似,不同的是Lift值和RPP是反方向变化的,这才形成Lift 曲线与ROC曲线相反的形式。
节选谭磊所著的自《大数据挖掘》一书。未完待续……