Project Euler Problem 51-70
题目翻译是从 欧拉计划 | Project Euler 中文翻译站上面Copy 的
Problem 51 Prime digit replacements
通过置换*3的第一位得到的9个数中,有六个是质数:13,23,43,53,73和83。
通过用同样的数字置换56**3的第三位和第四位,这个五位数是第一个能够得到七个质数的数字,得到的质数是:56003, 56113, 56333, 56443, 56663, 56773, 和 56993。因此其中最小的56003就是具有这个性质的最小的质数。
找出最小的质数,通过用同样的数字置换其中的一部分(不一定是相邻的部分),能够得到八个质数。
解:
没什么说的,前51-100 暴力基本可解,所以这题也一样,只不过直接照题意解会很麻烦。实际上用同样的数字替换可通过枚举加全部由0、1构成的五位数来做,就比较简单,5位0、1组成的数细想一下还可以剪枝。
#include<iostream>
using namespace std;
const int limit=1000005;
bool bprime[limit]= {0};
int dif[]= {1 , 10 , 11 , 100 , 101 , 110 , 111 , 1000 , 1001 , 1010 , 1011 , 1100 , 1101 , 1110 ,1111 , 10000 , 10001 , 10010 , 10011 , 10100 , 10101 , 10110 , 10111 , 11000 , 11001 , 11010 ,11011 , 11100 , 11101 , 11110 , 11111 , 100000 , 100001 , 100010 , 100011 , 100100 , 100101 ,100110 , 100111 , 101000 , 101001 , 101010 , 101011 , 101100 , 101101 , 101110 , 101111 ,110000 , 110001 , 110010 , 110011 , 110100 , 110101 , 110110 , 110111 , 111000 , 111001 ,111010 , 111011 , 111100 , 111101 , 111110 , 111111 };
bool may(int n)
{
while(n)
{
if(n%10<=2)
return true;
n/=10;
}
return false;
}
bool can(int a,int b)// a is a prime number, b is the difference
{
if(a<b) return false;
int cnt=0,n=a,m=b,t=-1;
while(t==-1)
{
if(b%10)
{
t=a%10;
break;
}
a/=10,b/=10;
}
while(b)
{
if(b%10&&a%10!=t) return false;
a/=10,b/=10;
}
for(int i=t; i<10; i++)
{
if(n<limit&&!bprime[n]) ++cnt;
n+=m;
}
return cnt>=8;
}
int main()
{
bprime[0]=bprime[1]=true;
for(int i=2; i<2001; i++)
if(!bprime[i])
for(int j=i<<1; j<limit; j+=i)
bprime[j]=true;
for(int i=2; i<limit; i++)
if(!bprime[i]&&may(i))
for(int j=0; j<0x3f; j++)
if(can(i,dif[j]))
{
cout<<i<<" "<<dif[j]<<endl;
return 0;
}
return 0;
}
Problem 52 Permuted multiples
125874和它的二倍,251748, 包含着同样的数字,只是顺序不同。找出最小的正整数x,使得 2x, 3x, 4x, 5x, 和6x都包含同样的数字。用Python来的直接点
flag=True i=1 while flag: if set(str(i))==set(str(i*2))==set(str(i*3))==set(str(i*4))==set(str(i*5))==set(str(i*6)) and len(str(i))==len(str(i*6)): print i flag=False i+=1Problem 53 Combinatoric selections
从五个数12345中选出三个数一共有十种方法:123, 124, 125, 134, 135, 145, 234, 235, 245, and 345在组合数学中我们用5C3 = 10来表示.概括来说:
| nCr = |
n!
r!(nr)! |
,其中r n, n! = n(n1)...321, 并且0! = 1.n = 23时产生第一个超过一百万的数: 23C10 = 1144066.对于nCr, 1 n 100,有多少超过100万的值?包括重复的在内。 |
没什么难度的,递推就行
#include<iostream>
using namespace std;
int C[105][105]={0};
const int limit=101;
int main()
{
for(int i=0;i<limit;i++)
C[i][0]=C[i][i]=1;
for(int i=1;i<limit;i++)
for(int j=0;j<=i;j++)
{
C[i][j]=C[i-1][j]+C[i-1][j-1];
if(C[i][j]>1000000)
C[i][j]=1000001;
}
int ans=0;
for(int i=1;i<limit;i++)
for(int j=1;j<i;j++)
if(C[i][j]>=1000000)
ans++;
cout<<ans<<endl;
return 0;
}
Problem 54 Poker hands
在扑克游戏中,一局牌由五张牌组成,组成的牌的大小由低向高如下:
High Card: 最高值的牌.
One Pair: 两张面值一样的牌.
Two Pairs: 两个值不同的One Pair.
Three of a Kind: 三张面值一样的牌.
Straight: 所有的牌面值为连续数值.
Flush: 所有的牌花色相同.
Full House: Three of a Kind 加一个One Pair.
Four of a Kind: 四张牌面值相同.
Straight Flush: 所有的牌花色相同并且为连续数值.
Royal Flush: 10,J,Q,K和A,并且为相同花色。
牌的面值大小排序如下:
2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, King, Ace.
如果两个玩家的牌具有同样的排序(上面介绍的几种),那么他们牌的大小由手中最大的牌决定。例如,一对8比一对5大(见下面例一);但是如果两个玩家都用一对Q,那么他们手中最大的牌就用来比较大小(见下面例四);如果他们最高面值的牌也相等,那么就用次高面值的牌比较,以此类推。
考虑下面的几个例子:
局 玩家 1 玩家 2 胜利者
1 5H 5C 6S 7S KD 2C 3S 8S 8D TD 玩家 2
一对5 一对8
2 5D 8C 9S JS AC2C 5C 7D 8S QH 玩家 1
最大面值牌A 最大面值牌Q
3 2D 9C AS AH AC3D 6D 7D TD QD 玩家 2
三个A 方片Flush
4 4D 6S 9H QH QC3D 6D 7H QD QS 玩家 1
一对Q,最大牌9 一对Q,最大牌7
5 2H 2D 4C 4D 4S3C 3D 3S 9S 9D
三个4的Full House三个3的Full House 玩家 1
文件 poker.txt 包含一千局随机牌。每一行包含十张牌(用空格分隔);前五张是玩家1的牌,后五张是玩家2的牌。 所有的牌都是合理的(没有非法字符或者重复的牌)。每个玩家的牌没有顺序,并且每一局都有明确的输赢。
其中玩家1能赢多少局?
恶心题,模拟下就行
#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
#define JoinValues(v,x) ((v<<20)+(x[4]/10<<16)+(x[3]/10<<12)+(x[2]/10<<8)+(x[1]/10<<4)+x[0]/10)
int charValue[128]={0};
int inline getValue(char a,char b)
{
return charValue[int(a)]*10+charValue[int(b)];
}
int A[5],B[5];
int getCardsValue(int C[])
{
sort(C,C+5);
bool flag=true; ///Royal Flush or Straight Flush
for(int i=1;i<5;i++)
if(C[i]-C[i-1]!=10) flag=false;
if(flag) return JoinValues(10,C);
if(C[3]/10==C[0]/10||C[4]/10==C[1]/10) ///Four of a kind
return (8<<20)+C[2];
if((C[0]/10==C[1]/10&&C[2]/10==C[4]/10)||(C[0]/10==C[2]/10&&C[3]/10==C[4]/10)) ///Full House
return (7<<20)+C[2];
flag=true;///Flush
for(int i=1;i<5;i++)
if(C[i]%10!=C[0]%10) flag=false;
if(flag) return JoinValues(6,C);
flag=true; ///Straight
for(int i=1;i<5;i++)
if(C[i]/10-C[i-1]/10!=1) flag=false;
if(flag) return JoinValues(5,C);
if(C[0]/10==C[2]/10||C[1]/10==C[3]/10||C[2]/10==C[4]/10)///three of a Kind
return (4<<20)+C[2];
int cnt=0; ///Two Pairs
for(int i=1;i<5;i++)
if(C[i]/10==C[i-1]/10)
cnt++;
if(cnt==2)
{
if(C[4]/10!=C[3]/10) swap(C[4],C[2]);
if(C[2]/10!=C[1]/10) swap(C[0],C[2]);
return JoinValues(3,C);
}
if(cnt==1) /// one Pair
{
cnt=0;
int tmp[5];
for(int i=0;i<4;i++)
if(C[i]/10==C[i+1]/10) tmp[4]=tmp[3]=C[i];
for(int i=0;i<5;i++)
if(C[i]/10!=tmp[4]/10)
tmp[cnt++]=C[i];
return JoinValues(1,tmp);
}
///HighCard
return JoinValues(0,C);
}
int main()
{
freopen("p054_poker.txt","r",stdin);
for(int i='0';i<='9';i++)
charValue[i]=i-int('0');
charValue[int('T')]=10;
charValue[int('J')]=11;
charValue[int('Q')]=12;
charValue[int('K')]=13;
charValue[int('A')]=14;
charValue[int('C')]=0;
charValue[int('D')]=1;
charValue[int('S')]=2;
charValue[int('H')]=3;
int ans=0;
string str;
while(cin>>str)
{
A[0]=getValue(str[0],str[1]);
for(int i=1;i<5;i++)
{
cin>>str;
A[i]=getValue(str[0],str[1]);
}
for(int i=0;i<5;i++)
{
cin>>str;
B[i]=getValue(str[0],str[1]);
}
if(getCardsValue(A)>getCardsValue(B)) ans++;
}
cout<<ans<<endl;
return 0;
}
Problem 55 Lychrel numbers
我们将47与它的逆转相加,47 + 74 = 121, 可以得到一个回文。
并不是所有数都能这么快产生回文,例如:
349 + 943 = 1292,
1292 + 2921 = 4213
4213 + 3124 = 7337
也就是说349需要三次迭代才能产生一个回文。
虽然还没有被证明,人们认为一些数字永远不会产生回文,例如196。那些永远不能通过上面的方法(逆转然后相加)产生回文的数字叫做Lychrel数。因为这些数字的理论本质,同时也为了这道题,我们认为一个数如果不能被证明的不是Lychrel数的话,那么它就是Lychre数。此外,对于每个一万以下的数字,你还有以下已知条件:这个数如果不能在50次迭代以内得到一个回文,那么就算用尽现有的所有运算能力也永远不会得到。10677是第一个需要50次以上迭代得到回文的数,它可以通过53次迭代得到一个28位的回文:4668731596684224866951378664。
令人惊奇的是,有一些回文数本身也是Lychrel数,第一个例子是4994。
10000以下一共有多少个Lychrel数?
又是暴力。
>>> def isLyc(n): for i in xrange(51): n=int(n+int(str(n)[::-1])) if str(n)==str(n)[::-1]: return True return False >>> ans =0 >>> for i in xrange(1,10001): if isLyc(i): ans+=1 >>> ans 249
Problem 56 Powerful digit sum
一个googol (10^100)是一个巨大的数字:1后面跟着100个0;100^100几乎是不可想象的大:1后面跟着200个0。它们虽然很大,但是它们的各位数之和却只有1。
考虑形如 a^b 的数, 其中 a, b < 100,最大的各位和是多少?
max([sum([int(x) for x in str(a**b)]) for a in xrange(1,101) for b in xrange(1,101)])
Problem 57 Square root convergents
2的平方根可以被表示为无限延伸的分数:
√ 2 = 1 + 1/(2 + 1/(2 + 1/(2 + ... ))) = 1.414213...
将其前四次迭代展开,我们得到:
1 + 1/2 = 3/2 = 1.5
1 + 1/(2 + 1/2) = 7/5 = 1.4
1 + 1/(2 + 1/(2 + 1/2)) = 17/12 = 1.41666...
1 + 1/(2 + 1/(2 + 1/(2 + 1/2))) = 41/29 = 1.41379...
接下来三次迭代的展开是99/70, 239/169, and 577/408, 但是第八次迭代的展开, 1393/985, 是第一个分子的位数超过分母的位数的例子。
在前1000次迭代的展开中,有多少个的分子位数超过分母位数?
连分数的题目,还有几个和这个一个类型的,这个简单因为迭代式给出了
>>> def nxt(): a,b,i=1,2,0 while i<1000: yield [a+b,b] a=b*2+a a,b=b,a i+=1 >>> ans=0 >>> for x in [x for x in nxt()]: if len(str(x[0])) > len(str(x[1])): ans+=1 >>> ans 153Problem 58 Spiral primes
从1开始逆时针旋转,可以得到一个边长为7的螺旋正方形。
37 36 35 34 33 32 31
38 17 16 15 14 13 30
39 18 5 4 3 12 29
40 19 6 1 2 11 28
41 20 7 8 9 10 27
42 21 22 23 24 25 26
43 44 45 46 47 48 49
有趣的是奇数的平方数都处于右下对角线上。更有趣的是,对角线上的13个数字中有8个质数,其百分比是8/13 ≈ 62%。
如果在上面的螺旋正方形上再加一层,可以得到一个边长为9的螺旋正方形。如果这个过程继续,到螺旋正方形的边长为多少时,对角线上的质数百分比第一次降到10%以下?直接找规律得出公式,就行
#include<iostream>
#include<stdio.h>
using namespace std;
const long long limit=10000000;
bool bprime[limit]={0};
int prime[limit/10],nprime=0;
bool inline isprime(long long n)
{
if(n<limit) return bprime[n]==false;
for(long long i=0;prime[i]*prime[i]<=n;i++)
if(n%prime[i]==0) return false;
return true;
}
long long tmp;
int main()
{
for(int i=2;i<10000;i++)
if(!bprime[i])
for(int j=i<<1;j<limit;j+=i)
bprime[j]=true;
for(int i=2;i<limit;i++)
if(!bprime[i])
prime[nprime++]=i;
int all=5,ok=3;
long long i;
for(i=2;;i++)
{
tmp=(i*2+1)*(i*2+1);
if(isprime(tmp-i*2)) ok++;
if(isprime(tmp-i*4)) ok++;
if(isprime(tmp-i*6)) ok++;
all+=4;
if(ok*10<all)
{
cout<<(i*2+1)<<endl;
break;
}
}
return 0;
}
Problem 59 XOR decryption
电脑上的每个字符都有一个唯一编码,通用的标准是ASCII (American Standard Code for Information Interchange 美国信息交换标准编码)。例如大写A = 65, 星号(*) = 42,小写k = 107。
一种现代加密方法是用一个密钥中的给定值,与一个文本文件中字符的ASCII值进行异或。使用异或方法的好处是对密文使用同样的加密密钥可以得到加密前的内容。例如,65 XOR 42 = 107, 然后 107 XOR 42 = 65。
对于不可攻破的加密,密钥的长度与明文信息的长度是一样的,而且密钥是由随机的字节组成的。用户将加密信息和加密密钥保存在不同地方,只有在两部分都得到的情况下,信息才能被解密。
不幸的是,这种方法对于大部分用户来说是不实用的。所以一种修改后的方案是使用一个密码作为密钥。如果密码比信息短,那么就将其不断循环直到明文的长度。平衡点在于密码要足够长来保证安全性,但是又要足够短使用户能够记得。
你的任务很简单,因为加密密钥是由三个小写字母组成的。文件 cipher1.txt (右键另存为)包含了加密后的ASCII码,并且已知明文是由常用英语单词组成。使用该文件来解密信息,然后算出明文中字符的ASCII码之和
文章如果是常用的英语词组成的,可以直接判断是否出现那些常用的单词,the to of that is 等,或者按字母频率统计等,不过从论坛来看找the的
比较多。另外,多试几下就差不多了
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;
#define MAXN 10000
char chr[MAXN],key[4],ch;
int data[MAXN],cnt=0,tmp,i;
bool check()
{
string text(chr);
if(text.find(".")==string::npos) return false;
if(text.find(",")==string::npos) return false;
if(text.find("the")==string::npos) return false;
if(text.find("that")==string::npos) return false;
if(text.find("is")==string::npos) return false;
if(text.find("in")==string::npos) return false;
if(text.find("to")==string::npos) return false;
if(text.find("it")==string::npos) return false;
return true;
}
int main()
{
freopen("p059_cipher.txt","r",stdin);
while(cin>>data[cnt++]>>ch);
chr[cnt]=key[3]='\0';
for(key[0] = 'a'; key[0]<='z'; key[0]++)
for(key[1] = 'a'; key[1]<='z'; key[1]++)
for(key[2] = 'a'; key[2]<='z'; key[2]++) //31 ~126
{
for(i=0; i<cnt; i++)
{
chr[i]=(char)(data[i]^(int)key[i%3]|32);
if(chr[i]<' '||chr[i]>'~') break;
}
if(i==cnt&&check())
cout<<key<<endl;
}
return 0;
}
Problem 60 Prime pair sets
质数3, 7, 109, 和 673是值得注意的。将其中任意两个质数以任何顺序相连接产生的结果都是质数。例如,取7和109,连接而成的7109和1097都是质数。这四个质数的和是792,这也是满足这个性质的四个质数集合的最小总和。
找出满足这个性质的五个质数的集合中,集合数之和最小的。算出这个最小的和。
Brute-Force ,够慢的9 sec 不过还有更慢的
#include<iostream>
#include<stdio.h>
#include<set>
#include<map>
#include<algorithm>
using namespace std;
const int limit=100000001;
bool bprime[limit]= {0};
int prime[11010],nprime=0;
struct Edge
{
int x,y;
bool operator < (const Edge & b) const
{
return this->x < b.x;
}
Edge(int a=0,int b=0):x(a),y(b) {}
} data[40000];
int cnt=0;
int check(int a,int b,int c,int d,int e)
{
int num[5]= {a,b,c,d,e};
for(int i=0; i<5; i++)
for(int j=0; j<5; j++)
{
if(i==j) continue;
int tmp=num[i];
int ans=num[j];
while(tmp)
{
ans*=10;
tmp/=10;
}
ans+=num[i];
if (ans>=limit||bprime[ans]) return false;
}
return true;
}
bool bingo(int ary[],int n)
{
int a=0;
for(int b=a+1; b<n; b++)
for(int c=b+1; c<n; c++)
for(int d=c+1; d<n; d++)
for(int e=d+1; e<n; e++)
if(check(ary[a],ary[b],ary[c],ary[d],ary[e]))
{
cout<<ary[a]<<" "<<ary[b]<<" "<<ary[c]<<" "<<ary[d]<<" "<<ary[e]<<endl;
cout<<ary[a]+ary[b]+ary[c]+ary[d]+ary[e]<<endl;
return true;
}
return false;
}
bool ok(int a,int b)
{
int tmp=a,n=b;
while(n)
{
tmp*=10;
n/=10;
}
tmp+=b;
if(bprime[tmp]) return false;
tmp=b,n=a;
while(n)
{
tmp*=10;
n/=10;
}
tmp+=a;
return !bprime[tmp];
}
set<int> se;
int main()
{
//freopen("out.txt","w",stdout);
bprime[0]=bprime[1]=true;
for(int i=2; i<10000; i++)
if(!bprime[i])
for(int j=i<<1; j<limit; j+=i)
bprime[j]=true;
for(int i=2; i<10000; i++)
if(!bprime[i])
prime[nprime++]=i;
int ans=0;
for(int i=0; i<nprime; i++)
for(int j=i+1; j<nprime; j++)
if(ok(prime[i],prime[j]))
{
data[cnt++]=Edge(prime[i],prime[j]);
//data[cnt++]=Edge(prime[j],prime[i]);
}
sort(data,data+cnt);
int i=0;
int ary[400],n;
while(i<cnt)
{
se.clear();
int x=data[i].x;
se.insert(x);
while(data[i].x==x)
se.insert(data[i++].y);
n=0;
for(set<int>::const_iterator it=se.begin(); it!=se.end(); ++it)
ary[n++]=*it;
if(bingo(ary,n))
return 0;
}
return 0;
}
/***
13 5197 5701 6733 8389
26033
about 9 seconds
***/
Problem 61 Cyclical figurate numbers
三角形数,四角形数,五角形数,六角形数,七角形数和八角形数都是定形数,他们分别由以下公式产生:
三角形数 P3,n=n(n+1)/21, 3, 6, 10, 15, ...
四角形数 P4,n=n^2 1, 4, 9, 16, 25, ...
五角形数 P5,n=n(3n−1)/21, 5, 12, 22, 35, ...
六角形数 P6,n=n(2n−1)1, 6, 15, 28, 45, ...
七角形数 P7,n=n(5n−3)/21, 7, 18, 34, 55, ...
八角形数 P8,n=n(3n−2)1, 8, 21, 40, 65, ...
三个四位数形成的有序集合: 8128, 2882, 8281,有三个有趣的性质:
这个集合是循环的:每个数的后两位数是下一个数的前两位数,包括第三个和第一个的关系。
三种定形数中的每一种都能被这三个数中的一个不同的数代表:三角形数 (P3,127=8128), 四角形数 (P4,91=8281), 和五角形数 (P5,44=2882)。
这是唯一具有以上性质的四位数的集合。
找出唯一的一个六个四位数的循环集合,使得从三角形数到八角形数中的每一种都能由该集合中的一个不同的数代表。
求这个集合中元素之和。
暴力没得说
#include<iostream>
using namespace std;
inline int cal(int n,int i)
{
if(i<=4)
return i==3?(n+1)*n/2:n*n;//3 4
if(i>6)
return i==7?n*(5*n-3)/2:n*(3*n-2);//7 8
return i==5?n*(3*n-1)/2:n*(2*n-1);//5 6
}
int rs[9][2]= {0,0,0,0,0,0,45,141,32,100,26,82,23,71,21,64,19,59};
bool used[10]= {0},goon=true;
int num[10],cnt=0,seq[10],nn[10];
void dfs()
{
if(!goon) return ;
if(cnt==6)
{
for(int i=0; i<6; i++)
if(num[i]%100!=num[(i+1)%6]/100)
return ;
goon=false;
int ans=0;
for(int i=0; i<6; i++)
{
cout<<num[i]<<" "<<seq[i]<<" "<<nn[i]<<" "<<endl;
ans+=num[i];
}
cout<<"sum "<<ans<<endl;
}
for(int i=8; i>2; i--)
if(!used[i])
{
used[i]=true;
seq[cnt]=i;
for(int j=rs[i][0]; j<rs[i][1]; j++)
{
nn[cnt]=j;
num[cnt++]=cal(j,i);
if(cnt>1&&num[cnt-2]%100==num[cnt-1]/100)
dfs();
else if(cnt==1)
dfs();
--cnt;
}
used[i]=false;
}
}
int main()
{
dfs();
return 0;
}
/****
if(i==3) return (n+1)*n/2;
if(i==4) return n*n;
if(i==5) return n*(3*n-1)/2;
if(i==6) return n*(2*n-1);
if(i==7) return n*(5*n-1)/2;
if(i==8) return n*(3*n-2);
***/
/***
45 141
32 100
26 82
23 71
21 64
19 59
***/
立方数 41063625 (345^3) 通过排列可以得到两个另外的立方数: 56623104 (384^3) 和 66430125 (405^3)。 实际上41063625是最小的三个(不多不少)排列是立方数的立方数。
找出最小的立方数,其五个(不多不少)排列是立方数。
def change(n):
tmp='1'
for x in sorted(str(n)):
tmp+=x
return int(tmp)
mp={}
limit=10000
ans=0
for x in xrange(1,limit):
tmp=change(x**3)
if tmp in mp and mp[tmp]==4:
#print x
ans=x
break
elif tmp in mp:
mp[tmp]+=1
else :
mp[tmp]=1
for x in xrange(1,10000):
if change(x**3)==change(ans**3):
print x,x**3
#break
Problem 63 Powerful digit counts
五位数16807=7^5 同时也是一个数的五次方。类似的,九位数 134217728=8^9,同时也是一个数的九次方。
有多少n位正整数同时也是某个数的n次方?
print len([(x,y) for x in range(1,10) for y in range(1,50) if len(str(x**y))==y])
10000以下的连分数中有多少拥有奇数周期?具体可以WIKI有定理,我是直接写了一个有理数类和一个分数类,模拟了
#include<iostream>
#include<math.h>
#include<map>
#include<algorithm>
using namespace std;
struct Num
{
int rt,in,tim;/// = tim*sqrt(rt)+in
Num(int r=0,int i=0,int t=0):rt(r),in(i),tim(t) {};
double getValue()
{
return tim*sqrt(rt)+in;
}
Num operator /(const int & t)const
{
return Num(this->rt,this->in/t,this->tim/t).normal();
}
Num operator *(const Num & t)const
{
if(this->rt!=t.rt&&this->rt!=0&&t.rt!=0)
{
cout<<"Error"<<endl;
return Num();
}
int r=this->rt;
if(r==0) r=t.rt;
return Num(r,this->in*t.in+this->tim*t.tim*this->rt,this->tim*t.in+t.tim*this->in).normal();
}
Num operator *(const int & t)const
{
return Num(this->rt,this->in*t,this->tim*t);
}
Num operator -(const int & t)const
{
return Num(this->rt,this->in-t,this->tim);
}
Num operator -(const Num & b)const
{
int tmp=this->rt;
if(b.rt!=0) tmp=b.rt;
return Num(tmp,this->in-b.in,this->tim-b.tim).normal();
}
Num normal()
{
if(this->tim==0||this->rt==0) this->rt=this->tim=0;
return *this;
}
void output(char ch)
{
cout<<ch<<": "<<rt<<" "<<in<<" "<<tim<<endl;
}
bool operator<(const Num & n)const
{
if(this->tim==n.tim)
return this->in<n.in;
return this->tim<n.tim;
}
bool operator ==(const Num& n) const
{
return !(*this<n||n<*this);
}
};
int gcd(int a,int b)
{
if(a<0) a=-a;
if(b<0) b=-b;
if(a<b) swap(a,b);
return b==0?a:gcd(b,a%b);
}
struct Fra
{
Num a,b;/// a/b=numerator/denominator
Fra(int _a=0,int _b=0):a(_a,0,1),b(0,_b,0){}
int getValue()
{
int val=a.getValue()/b.getValue();
a=a-b*val;
swap(a,b);
if(b.tim)
{
a=a*Num(b.rt,-b.in,b.tim);
b=b*Num(b.rt,-b.in,b.tim);
}
int tmp=gcd(gcd(a.tim,a.in),gcd(b.tim,b.in));
if(tmp==0) return -1;
a=a/tmp;
b=b/tmp;
return val;
}
bool operator <(const Fra& f )const
{
if(this->a==f.a)
return this->b<f.b;
return this->a<f.a;
}
};
int main()
{
int ans=0;
for(int i=1;i<=10000;i++)
{
map<Fra,int> mp;
Fra n(i,1);
for(int j=1;;j++)
{
int tmp=mp[n];
if(tmp!=0)
{
if((j-tmp)&1) ans++;
break;
}
mp[n]=j;
if(n.getValue()==-1) break;
}
}
cout<<ans<<endl;
return 0;
}
Problem 65 Convergents of e
找出e的连分数中第100个收敛项的分子各位之和。
def cal(k): ls=[2] for x in range(1,k+1): ls.append(1) ls.append(2*x) ls.append(1) ls=ls[::-1] a,b=0,1 for x in ls: a,b=b,a+b*x return (b,a) print sum([int(x) for x in str(cal(33)[0])])Problem 65 Diophantine equation
考虑如下形式的二次丢番图方程:
x^2 – Dy^2 = 1
例如当 D=13时, x 的最小解是 6492 – 13×1802 = 1.
可以认为当D时平方数时方程无正整数解。
通过寻找当D = {2, 3, 5, 6, 7}时 x 的最小解,我们得到:
3^2 – 2×2^2 = 1
2^2 – 3×1^2 = 1
9^2 – 5×4^2 = 1
5^2 – 6×2^2 = 1
8^2 – 7×3^2 = 1
因此对于D ≤ 7, x 的最小解的最大值在D=5时取到。
找出D ≤ 1000中使得 x 的最小值取到最大的D的值。
丢番图方程具体WIKI, 我是看的别人的博客代码就不贴了
Problem 67 Maximum path sum II
从以下三角形的顶端开始,向下一行的相邻数字移动,从顶端到底端的最大总和是23。
3
7 4
2 4 6
8 5 9 3
也就是 3 + 7 + 4 + 9 = 23.
triangle.txt (右键另存为)是一个文本文件,包含了一个一百行的三角形,找出这个三角形中从顶到底的最大和。
注意:这是题目18的更难的一个版本。穷举每一种可能的路径是不可行的,因为一共有299条可能的路径。就算每秒钟能处理1012条路径,也需要200亿年来处理完所有的路径。存在一个高效的方法来处理这道题。
基础动态规划
#include<iostream>
#include<stdio.h>
using namespace std;
int data[200][200];
int main()
{
freopen("in.txt","r",stdin);
for(int i=0;i<100;i++)
for(int j=0;j<=i;j++)
cin>>data[i][j];
for(int i=100-2;i>=0;i--)
for(int j=0;j<=i;j++)
data[i][j]+=max(data[i+1][j],data[i+1][j+1]);
cout<<data[0][0]<<endl;
return 0;
}
Problem 68 Magic 5-gon ring
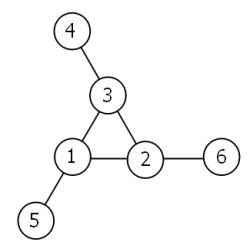
考虑如下的“魔术”三角环:该环被1到6的数字填充,并且每一行的和为9。
按照顺时针顺序,从外部节点最小的三个为一组的组开始(该例中为4,3,2),每一组解都可以被唯一描述。例如,上图所示的解可以被描述为集合: 4,3,2; 6,2,1; 5,1,3。这个环还可以被用四个不同的和来完成。一共有八组解。
| 和 | 解 |
| 9 | 4,2,3; 5,3,1; 6,1,2 |
| 9 | 4,3,2; 6,2,1; 5,1,3 |
| 10 | 2,3,5; 4,5,1; 6,1,3 |
| 10 | 2,5,3; 6,3,1; 4,1,5 |
| 11 | 1,4,6; 3,6,2; 5,2,4 |
| 11 | 1,6,4; 5,4,2; 3,2,6 |
| 12 | 1,5,6; 2,6,4; 3,4,5 |
| 12 | 1,6,5; 3,5,4; 2,4,6 |
将每组解的数字连接起来,可以得到一个9位的字符串;三角环所能形成的最大字符串为432621513。使用数字1到10,通过不同的安排,可以得到16位或17位的字符串。五角环所能形成的最大的16位的字符串是什么?
没什么说的,还是暴力
#include<iostream>
#include<algorithm>
#include<time.h>
using namespace std;
int num[10]= {1,2,3,4,5,6,7,8,9,10},tmp;
int seq[]= {0,5,6,1,6,7,2,7,8,3,8,9,4,9,5};
long long ans=0,temp;
void deal()//get the string
{
temp=0;
for(int i=1; i<5; i++)
if(num[i]<num[0]) return ;
for(int i=0; i<15; i++)
{
if(num[seq[i]]==10) temp*=10;
temp=temp*10+num[seq[i]];
}
if(temp>ans&&temp<9999999999999999L) ans=temp;
}
int main()
{
int start=clock();
for(int i=0; i<3628800; i++)
{
tmp=num[0]+num[5]+num[6];
if(tmp==num[1]+num[6]+num[7]&&
tmp==num[2]+num[7]+num[8]&&
tmp==num[3]+num[8]+num[9]&&
tmp==num[4]+num[9]+num[5])
deal();
next_permutation(num,num+10);
}
cout<<ans<<endl;
cout<<clock()-start<<endl;
return 0;
}
/***
0
\ 1
5 ___ /
/ 6
9 |
/ \ /
/ 8____7____2
4 \
\
3
the positions' number in my code
***/
Problem 69 Totient maximum
欧拉函数φ(n)(有时也叫做phi函数)可以用来计算小于n 的数字中与n互质的数字的个数。例如,因为1,2,4,5,7,8全部小于9并且与9互质,所以φ(9)=6。
| n | 互质数 |
φ(n) | n/φ(n) |
| 2 | 1 | 1 | 2 |
| 3 | 1,2 | 2 | 1.5 |
| 4 | 1,3 | 2 | 2 |
| 5 | 1,2,3,4 | 4 | 1.25 |
| 6 | 1,5 | 2 | 3 |
| 7 | 1,2,3,4,5,6 | 6 | 1.1666... |
| 8 | 1,3,5,7 | 4 | 2 |
| 9 | 1,2,4,5,7,8 | 6 | 1.5 |
| 10 | 1,3,7,9 | 4 | 2.5 |
可以看出对于n 10,n=6时 的n/φ(n)取到最大值。找出 n 1,000,000 的 n 中使得n/φ(n)取到最大的 n 值。
#include<iostream>
using namespace std;
int euler(int n)
{
long long ans=n;
for(int i=2;i*i<=n;i++)
{
if(n%i==0)
{
ans=ans*(i-1)/i;
while(n%i==0) n/=i;
}
}
if(n!=1)
ans=ans*(n-1)/n;
return ans;
}
int main()
{
double p=0,tmp;
int ans=0;
for(int i=2;i<1000001;i++)
{
tmp=i*1.0/(euler(i)*1.0);
if(p<tmp)
{
p=tmp;
ans=i;
}
}
cout<<ans<<endl;
return 0;
}
Problem 70 Totient permutation
欧拉函数φ(n)(有时也叫做phi函数)可以用来计算小于等于n 的数字中与n互质的数字的个数。例如,因为1,2,4,5,7,8全部小于9并且与9互质,所以φ(9)=6。
数字1被认为与每个正整数互质,所以 φ(1)=1。
有趣的是,φ(87109)=79180,可以看出87109是79180的一个排列。
对于1 < n < 107,并且φ(n)是 n 的一个排列的那些 n 中,使得 n/φ(n) 取到最小的 n 是多少?
一般来说n/φ(n) 要大则n的因子要少,所以就是暴力了
#include<iostream>
using namespace std;
const int limit=10000000;
bool bprime[limit]={0};
long long prime[limit/10],nprime=0;
double p=100;
int ans=12;
int cnt=0;
void inline check(int m,int n)
{
if(double(m)/double(n)> p) return;
int a[10]={0},b[10]={0},c=m,d=n;
while(m)
{
a[m%10]++;
m/=10;
}
while(n)
{
b[n%10]++;
n/=10;
}
for(int i=0;i<10;i++)
if(a[i]!=b[i]) return ;
p=double(c)/double(d);
ans=c;
}
int main()
{
for(int i=2;i<4000;i++)
if(!bprime[i])
for(int j=i<<1;j<limit;j+=i)
bprime[j]=true;
for(int i=2;i<limit;i++)
if(!bprime[i])
prime[nprime++]=i;
for(int i=0;i<nprime;i++)
for(int j=i;prime[i]*prime[j]<=limit;j++)
check(prime[i]*prime[j],(prime[i]-1)*(prime[j]-1));
cout<<ans<<endl;
return 0;
}