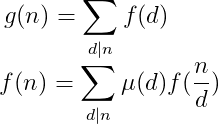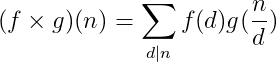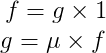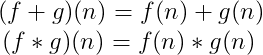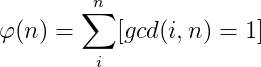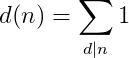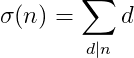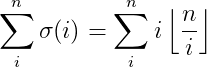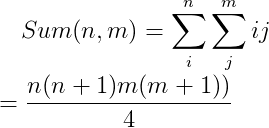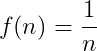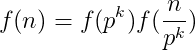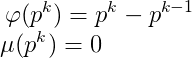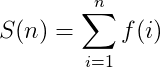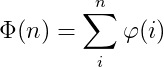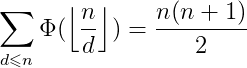【数论函数变换总结】【超长篇】【last update:2014-10-22】

最近被好多数论题虐翻……感觉学到了不少东西,总结一下

参考文献

数论函数变换 orz kAc http://pan.baidu.com/s/1mgn4oqO

数学常识 orz drcow http://pan.baidu.com/s/1mgGA4UO

积性函数..题目 orz jcvb http://jcvb.is-programmer.com/posts/41846.html

贾志鹏线性筛 orz jzp http://wenku.baidu.com/link?url=9spLgiNU8yom2-paqarcDfsbAzLUgyYwalwv7V5K8W-lGl4qS_seaX-NlOukspGTDltU1tVhNPlBF76QKtvnDyxDxl-wL6BRxVWiWGiFipm

莫比乌斯反演是指

狄利克雷卷积是指

所以莫比乌斯反演又可以写作

顺便定义一下

常见数论函数

欧拉函数

莫比乌斯函数

其他常见数论函数

常见变换

有了以上基础我们就来推式子了!!!

1D gcd sum

1..n中与n互质的数的个数

2D gcd sum

1..n和1..m中互质的数的对数

约数和之和

公约数约数和

1..n中与n互质的数的和

1D lcm sum

1..n与1..m所有数对的乘积和

1..n与1..m中互质的数对的乘积和

2D lcm sum level 1

我们定义一个函数

它不是整数……但很有用

顺手定义

即

2D lcm sum level 2

上面这个式子最后一行的Sum前面应该加上"(d)"= = 、

积性函数筛出来,分块统计

怎样分块统计?

n/d,m/d最多有sqrt(n)+sqrt(m)中取值

f是非分块统计部分的[i,j]的区间和

Sum代表的是一系列可以分块统计的函数

for(int i=1,j;i<=n;i=j+1){
	j=min(n/(n/i),m/(m/i));
	ans+=(f[j]-f[i-1])*(Sum(n/i,m/i));
}

怎样线性筛积性函数?

for(int i=2;i<maxn;i++){
	if(!p[i]){
		prime[++prime[0]]=i;
		//A
	}for(int j=1;j<=prime[0]&&i*prime[j]<maxn;j++){
		p[i*prime[j]]=1;
		if(i%prime[j]==0){
			//B
			break;
		}else{
			//C
		}
	}
}

欧拉筛把积性函数分成了三类

A:n为质数

B:n最小质因子为p且次数大于1

C:n最小质因子为p且次数为1
现在我们要计算一个积性函数

A:质数通常很简单,特判

C:显然i与p互质那么
B类比较复杂

但显然

所以我们记录n的最小质因子的幂

问题转化为如何求

这就与函数本身相关了

比如

对于2D lcm sum level 2

宇宙最快求和法

求

设

那么

在g函数前缀和O(1)计算的情况下,记忆化搜索可以证明复杂度是,小范围预处理会得到更好的复杂度

但是……

求

用上述方法是可以做的

不过具体数学说……

于是

真是太神了……有空再研究吧……

【未完待续】