数据挖掘十大经典算法之apriori算法&源代码
数据挖掘十大经典算法
国际权威的学术组织the IEEE International Conference on Data Mining
(ICDM) 2006年12月评选出了数据挖掘领域的十大经典算法:C4.5, k-Means,
SVM, Apriori, EM, PageRank, AdaBoost, kNN, Naive Bayes, and CART.
不仅仅是选中的十大算法,其实参加评选的18种算法,实际上随便拿出一种来都
可以称得上是经典算法,它们在数据挖掘领域都产生了极为深远的影响。
4. The Apriori algorithm
Apriori算法是一种最有影响的挖掘布尔关联规则频繁项集的算法。其核心是基于
两阶段频集思想的递推算法。该关联规则在分类上属于单维、单层、布尔关联规
则。在这里,所有支持度大于最小支持度的项集称为频繁项集,简称频集。
VC 界面的源代码见 http://download.csdn.net/source/2963738
由Agrawal等人提出的Apriori是经典的关联规则和频繁项集挖掘算法,围绕着它的改进和实现有大量的文献。该算法是挖掘产生布尔关联规则频繁项目集的经典算法,从其产生到现在对关联规则挖掘方面的研究有着很大的影响。
为了提高频繁项目的挖掘效率,Apriori算法利用了两个重要的性质,用于压缩搜索的空间。
【1】若X为频繁项目集,则X的所有子集都是频繁项目集。
【2】若X为非频繁项目集,则X的所有超集均为非频繁项目集。
Apriori算法的处理流程为:宽度优先搜索整个项集空间,从k=0开始,迭代产生长度为k+1的候选项集的集合Ck+1。候选项集是其所有子集都是频繁项集的项集。C1由I0中所有的项构成,在第k层产生所有长度为k+1的项集。这由两步完成:第一步,Fk自连接。将Fk中具有相同(k-1)-前缀的项集连接成长度为k的候选项集。第二步是剪枝,如果项集的所有长度为k的子集都在Fk中,该项集才能作为候选项集被加入Ck+1中。为了计算所有长度为k的候选项集的支持度,在数据库水平表示方式下,需要扫描数据库一遍。在每次扫描中,对数据库中的每条交易记录,为其中所包含的所有候选k-项集的支持度计数加1。所有频繁的k-项集被加入Fk中。此过程直至Ck+1等于空集时结束。
算法 Apriori
Input: Transaction DataBase D,Minimum support threshold minsup。
Output: Frequent pattern L
(1) L1=search_frequent_1-itemsets( D );
(2) for(k=2;Lk-1≠φ;k++) do
(3) begin
(4) Ck=apriori-gen(Lk-1);
(5) for all transactions t D do
(6) begin
(7) Ct=subset(Ck,t);
(8) for all candidates c Ct do
(9) c.count++;
(10) end
(11) Lk ={c Ck|c.count≥minsup}
(12) end
(13) Answer L=∪kLk;
Procedure Search_frequent_1-itemsets( D )
(1) begin
(2) for all transactions t D do
(3) begin
(4) for each item ik t do
(5) ik.count++;
(6) end
(7) L1 ={ i I | i.count≥minsup}
(8) return L1;
(9) end
Procedure apriori_gen(Lk)
(1) begin
(2) for each itemset l1 Lk do
(3) for each itemset l2 Lk do
(4) begin
(5) if ( l1[1]=l2[1]) ( l1[2]=l2[2]) … ( l1[k-1]=l2[k-1]) ( l1[k]<l2[k]) then
(6) begin
(7) c= l1 l2;
(8) if Is_include_infrenquent_subset(c,Lk) then
(9) delete c;
(10) else add c to Ck+1 ;
(11) end
(12) end
(13) return Ck+1 ;
(14) end
Procedure Is_include_infrenquent_subset(c,Lk)
(1)begin
(2) for each k-subset s of c
(3) if s Lk then
(4) reture TURE;
(5) return FALSE ;
(6)end
在主程序中,第一步首先扫描整个交易数据库D,统计每个项目(item)的支持数,计算其支持度,将支持度大于等于最小支持度minsup的项目构成的集合放入到L1 中;从第2步到第11步,用k-1频繁项目集构成的Lk-1生成候选集的集合Ck,以便从中生成Lk,其中apriori_gen函数(第4步)用来从Lk-1中生成Ck,然后对数据库进行扫描(第5步),对于数据库中的每一个交易,subset函数用来发现此交易包含的所有候选集(第7步),并为这些候选集的计数器加1(第8-9步)。最后满足minsup的候选集被放入到Lk中。
apriori_gen过程完成两种操作:并(join)和剪枝(prune)。在并运算步骤中,Lk-1 与Lk-1 进行并运算生成潜在的候选集(2-7步),条件l1[k-1]<l2[k-1]保证不会有重复的候选集生成(第5步)。在剪枝步骤中(8-10步),利用性质2.1,删除那些存在子集不是频繁项目集的候选集,测试子集是否为频繁项目集由过程Is_include_infrenquent_subset完成。
为了清楚的阐述Apriori算法的挖掘过程,现举例如下:
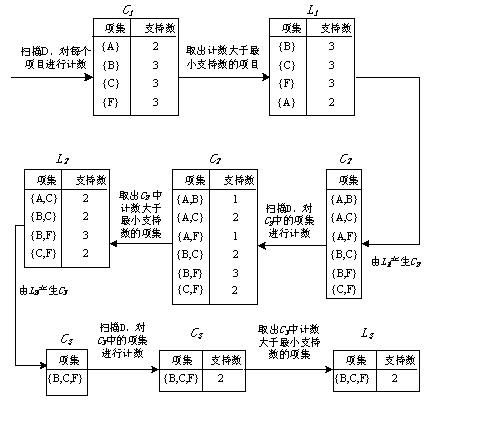
【例1】设事务数据库D如表2.1所示,D中包含4个事务,即|D|=4,最小支持数mincount=2,即最小支持度minsup=2/4=50%。挖掘频繁项目集的具体过程如下所述:C1={{A},{B},{C},{D},{F}},第一次循环产生L1={{A},{B},{C},{F}},由Apriori_gen(L1)生成C2,扫描数据库,计算C2中每个候选集得到L2。依此循环,得到L3。整个挖掘过程如图2.1所示。
表1 事务数据库D
| Tid |
事务 |
| 100 200 300 400 |
B,C,F A,C,D B,F A,B,C,F |
图1 Apriori算法的执行过程
在找到了事务数据库中的所有频繁项集后,利用这些频繁项集可以产生关联规则,产生关联规则的步骤如下:
(1) 对于每个频繁项目集l,产生l的所有非空子集。
(2) 对于l的每个非空子集m,如果support(l)/support(m)≥minconf,则输出规则“m (l-m)”。
例如,在上例中产生的频繁项目集l={B,C,F},l的非空子集有{B,C}、{B,F}、{C,F}、{B}、{C}和{F},则运用上述产生关联规则的方法可以得到以下关联规则:
B C F confidence=(2/4)/(4/4)=1
B F C confidence=(2/4)/(3/4)=0.667
C F B confidence=(2/4)/(2/4)=1
F B C confidence=(2/4)/(3/4)= 0.667
C B F confidence=(2/4)/(3/4)= 0.667
B C F confidence=(2/4)/(3/4)= 0.667
源代码 apriori.c
//////////////////////////////////////////////////////////////////////////
/*
*
*
*
* 文件名称:apriori.c
*
* 摘 要:apriori的最简单实现
*
* 当前版本:1.0
* 完成日期:2006.05
*
*/////////////////////////////////////////////////////////////////////////
#include<stdio.h>
typedef struct
{
int item[100]; //数据项
} D_Node; //数据库D
typedef struct
{
int item[100]; //数据项,用item[0]保存支持度
} C_Node; //候选集
typedef struct
{
int item[100]; //数据项,用item[0]保存支持度
} L_Node;//频繁集
C_Node C[100][100];
L_Node L[100][100];
D_Node D[100];
int min_supp; //最小支持度
void InPut()
{
int i,j,n,n1;
printf("请输入最小支持度:");
scanf("%d",&min_supp);
printf("请输入交易集的大小");
scanf("%d",&D[0].item[0]);
n=D[0].item[0];
for(i=1;i<=n;i++) //for1
{
printf("请输入交易[%d]中记录的个数(n)",i);
scanf("%d",&n1);
D[i].item[0]=n1;
for(j=1;j<=n1;j++) //for2
{
printf("请输入交易[%d]中记录项,直接输入数字:",i);
scanf("%d",&D[i].item[j]);
}//for2
} //for1
}//end of InPut
void C1()
{
//功能:扫描数据集D生成1项候选集C1
//输入:数据集D
//输出1项候选集C1
//初始条件 数据集D 非空
int i,j,k;
int no=1,temp=0;
C[1][0].item[0]=0; //1 项集的个数,在本算法中,用C[n][k].item[0]来保存候选集Cn的第k项的支持度
if(D[0].item[0]!=0)
{
C[1][1].item[1]=D[1].item[1];
}
for(i=1;i<=D[0].item[0];i++) //for1
{
for(j=1;j<=D[i].item[0];j++) //for2
{
temp=1;
for(k=1;k<=no;k++) //for3
{
if(C[1][k].item[1]==D[i].item[j])
{
C[1][k].item[0]++; //支持度加1
temp=0; //
} //if
}//end for3
if(temp)//生成新的项集
{
C[1][++no].item[1]=D[i].item[j];
C[1][no].item[0]=1;
}
}//end for2
} // end for1
C[1][0].item[0]=no;//数据项的个数
} //end of C1()
void Cn( int n)
{
//用频繁集Ln-1为基础,通过连接得到n项候选集Cn
int i,j,k,p,q,s,t,num;
int no=0,temp=0,count;
C[n][0].item[0]=0; //初始化
//printf("in Cn(%d) n=%d/n",n,n);
//printf("in Cn(%d) C[%d][0].item[0]=%d/n",n,n,C[n][0].item[0]);
num=L[n-1][0].item[0]; //num是Ln-1项集的数据个数
for(i=1;i<=num;i++)
for(j=i+1;j<=num;j++) //for2
{
temp=1; //测试是否满足联结条件
if(n>2)//if 1
{
for(k=1;k<n-1;k++) //for3
{
if(L[n-1][i].item[k]!=L[n-1][j].item[k])
{ temp=0;
break; }//if 1
}//end for3
}//end if1
if(temp==1)//满足联结条件
{
// printf("in if 2 no=%d/n",no);
no++;
for(p=1;p<=n-1;p++)
C[n][no].item[p]=L[n-1][i].item[p];
C[n][no].item[p]=L[n-1][j].item[p-1];
C[n][no].item[0]=0;
for(q=1;q<=D[0].item[0];q++) //for5 测试其支持度
{
count=0; //count用来记数,当所测试的项存在时,count加1,当count=n时,则子集存在
for(s=1;C[n][no].item[s]!=0;s++) //for6
{
for(t=1;t<=D[q].item[0];t++) //for7
{
if(C[n][no].item[s]==D[q].item[t])
{ count+=1;
break;
}
}//end for7
}//end for 6
if(count==n) C[n][no].item[0]+=1;//子集存在,第no项的支持度加1
}//end for5
C[n][0].item[0]+=1;
}//end if2
}//end for2
/* num=C[n][0].item[0];
printf("in Cn(%d) num=%d/n",n,num);
for(i=1;i<=num;i++)
for(j=0;j<=n;j++)
{
printf("in Cn(%d) C[%d][%d].item[%d]=%d/n",n,n,i,j,C[n][i].item[j]);
}
printf("in Cn(%d) C[%d][0].item[0]=%d/n",n,n,C[n][0].item[0]); */
}//end of Cn()
void L1()
{
int i,j,k;
j=0;
L[1][0].item[0]=0;
//printf("C[1][0].item[0]=%d/n",C[1][0].item[0]);
for(i=1;i<=C[1][0].item[0];i++)
{
if(C[1][i].item[0]>=min_supp)
{
j+=1;
for(k=1;k<=1;k++)
L[1][j].item[k]=C[1][i].item[k];
L[1][j].item[0]=C[1][i].item[0];
// printf("L[1][%d].item[1]=%d ",j,L[1][j].item[1]); 测试功能时加的
// printf(" -------------%d/n",L[1][j].item[0]);
}
}//end for1
L[1][0].item[0]=j;
}//end of L1()
void Ln(int n)
{
int i,j,k;
Cn(n);
j=0;
L[n][0].item[0]=0;
// printf("in Ln(%d) C[%d][0].item[0]=%d/n",n,n,C[n][0].item[0]);
for(i=1;i<=C[n][0].item[0];i++) //for 1
{
if(C[n][i].item[0]>=min_supp)
{
j+=1;
for(k=1;k<=n;k++)
L[n][j].item[k]=C[n][i].item[k];
L[n][j].item[0]=C[n][i].item[0];
} //end if
}//end for1
/* for(i=1;i<=j;i++)
for(k=0;k<=n;k++)
{printf("L[%d][%d].item[%d]=%d /n",n,i,k,L[n][i].item[k]);
} */
L[n][0].item[0]=j; //保存数据的个数
}//end of Ln(int n)
void OutPut(int n)
{
int i,j,k;
printf("频繁项目集L%d如下:/n",n);
k=L[n][0].item[0];
if(k!=0)
{
for(i=1;i<=k;i++)
{
printf("{");
for(j=1;j<=n;j++)
printf(" I%d ",L[n][i].item[j]);
printf("} 支持度:%d/n",L[n][i].item[0]);
}//for
}
else printf("项目集为空/n");
}
void main()
{
int i;
int n=1;
InPut();
C1();//初始化,生成1项候选集C1
L1();//得到1项频繁集L1
while(L[n][0].item[0]!=0)
{
n+=1;
Ln(n);
}
for(i=1;i<=n;i++)
OutPut(i);
char ch;
scanf("%d",&i);
}
--------------------------------------------------------------------------------------
FAST apriori.cpp
//////////////////////////////////////////////////////////////////////////
/*
*
*
*
* 文件名称:FAST apriori.cpp
*
* 摘 要:采用位运算提高算法的效率
*
* 当前版本:1.0
* 完成日期:2006.06.20
*
*/////////////////////////////////////////////////////////////////////////
#include <stdio.h>
#include <string.h>
typedef struct
{
char item[10]; //数据项
int min_supp_count;//最小支持度数
} C_Node; //候选集
typedef struct
{
char item[10]; //数据项
int min_supp_count;//最小支持度数
} L_Node; //频繁集
char D[10][10];
L_Node L[100];
C_Node C[100];
int min_supp_count=2;
int num=100;
void InPut()
{
strcpy(D[1],"abe");
strcpy(D[2],"bd");
strcpy(D[3],"bc");
strcpy(D[4],"abd");
strcpy(D[5],"ac");
strcpy(D[6],"bc");
strcpy(D[7],"ac");
strcpy(D[8],"abce");
strcpy(D[9],"abc");
}//end of InPut
int * DB=new int[num];
void suppDB()
{
int m='e';
int n;
int k;
for (int i=1;i<=9;i++)
{
n=strlen(D[i]);
DB [i]=0;
for (int j=0;j<n;j++)
{
k=1;
DB [i]+=k<<(int)(m-D[i][j]);
}
}
}
void check_supp(int num,int no)
{
int i,j,k,m;
int check;
m='e';
for(i=1;i<=num;i++)
{ check=0;
C[i].min_supp_count=0;
for (j=0;j<no;j++)
{
k=1;
check+=(int)(k<<(m-C[i].item[j]));
}
for (j=1;j<=9;j++)
{
if (check==(check&DB[j]))
{
C[i].min_supp_count+=1;//子集存在,支持度数加1
}
}
}
}
void C1()
{
//功能:扫描数据集D生成1项候选集C1
//输入:数据集D
//输出1项候选集C1
//初始条件 数据集D 非空
strcpy(C[1].item,"a");
strcpy(C[2].item,"b");
strcpy(C[3].item,"c");
strcpy(C[4].item,"d");
strcpy(C[5].item,"e");
C[0].min_supp_count=5; //1 项候选集的个数,在本算法中,用C[0].min_supp_count来保存候选集Cn的个数
check_supp(5,1);
} //end of C1()
void Cn( int n)
{
//用频繁集Ln-1为基础,通过连接得到n项候选集Cn
int i,j,k,p,num;
int no=0,temp=0;
C[0].min_supp_count=0; //初始化
num=L[0].min_supp_count; //num是Ln-1项集的数据个数
for(i=1;i<=num;i++)
for(j=i+1;j<=num;j++) //for2
{
temp=1; //测试是否满足联结条件
if(n>2)//if 1
{
for(k=0;k<n-2;k++) //for3
{
if(L[i].item[k]!=L[j].item[k])
{ temp=0;
break; }//if 1
}//end for3
}//end if1
if(temp==1)//满足联结条件
{
// printf("in if 2 no=%d/n",no);
no++;
for(p=0;p<=n-2;p++)
C[no].item[p]=L[i].item[p];
C[no].item[p]=L[j].item[p-1];
C[no].min_supp_count=0;
C[0].min_supp_count+=1;
}//end if2
}//end for2
num=C[0].min_supp_count;
check_supp(num,n);//测试支持度
}//end of Cn()
void L1()
{ int n=1;
int i,j,k;
j=0;
L[0].min_supp_count=0;//频繁集的个数,初始为0
for(i=1;i<=C[0].min_supp_count;i++)
{
if(C[i].min_supp_count>=min_supp_count)
{
j+=1;
strcpy(L[j].item,C[i].item);
L[j].min_supp_count=C[i].min_supp_count;
}
}//end for1
L[0].min_supp_count=j;///频繁集的个数,最后为j个
printf("频繁项目集L%d如下:/n",n);
k=L[0].min_supp_count;
if(k!=0)
{
for(i=1;i<=k;i++)
{
printf("{");
for(j=0;j<n;j++)
printf(" %c ",L[i].item[j]);
printf("} 支持度:%d/n",L[i].min_supp_count);
}//for
}
else printf("项目集为空/n");
}//end of L1()
void Ln(int n)
{
int i,j,k;
Cn(n);
j=0;
L[0].min_supp_count=0;
for(i=1;i<=C[0].min_supp_count;i++) //for 1
{
if(C[i].min_supp_count >=min_supp_count)
{
j+=1;
strcpy(L[j].item,C[i].item);
L[j].min_supp_count=C[i].min_supp_count;
} //end if
}//end for1
L[0].min_supp_count=j; //保存数据的个数
printf("频繁项目集L%d如下:/n",n);
k=L[0].min_supp_count;
if(k!=0)
{
for(i=1;i<=k;i++)
{
printf("{");
for(j=0;j<n;j++)
printf(" %c ",L[i].item[j]);
printf("} 支持度:%d/n",L[i].min_supp_count);
}//for
}
else printf("项目集为空/n");
}//end of Ln(int n)
void main()
{
int n=1;
InPut();
suppDB();
C1();//初始化,生成1项候选集C1
L1();//得到1项频繁集L1
while(L[0].min_supp_count!=0)
{
n+=1;
Ln(n);
}
char ch;
printf("press any key to eixe/n");
scanf("%c",&ch);
}