POJ3565 Ants【二分图最佳匹配】
题目链接:
http://poj.org/problem?id=3565
题目大意:
在坐标系中有N只蚂蚁,N棵苹果树,给你蚂蚁和苹果树的坐标。让每只蚂蚁去一棵苹果树,
一棵苹果树对应一只蚂蚁。这样就有N条直线路线,问:怎样分配,才能使总路程和最小,且
N条线不相交。
思路:
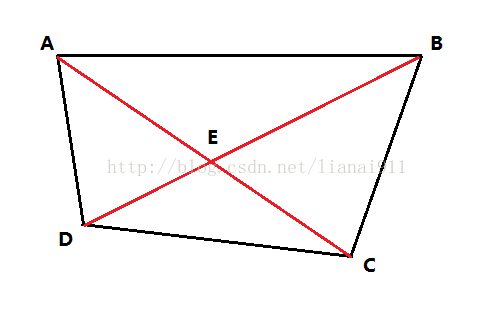
用一个图来说明思路。
假设A、B为蚂蚁,C、D为苹果树。则存在两种匹配:第一种是AD、BC,第二种是AC、BD。
根据三角形不等式AD+BC < AC+BD,最后得到很重要的一个性质——满足总路程之和最小
的方案一定不相交。现在来构建二分图,一边为蚂蚁,另一边为苹果树,以距离为边权值,题
目就变为了求带权二分图最小权和的最佳匹配。反向来思考,将距离乘以-1取负值建图,那么
就变为了求带权二分图最大权和的最佳匹配。直接用KM算法来做。KM模板参考博文:
http://blog.csdn.net/lianai911/article/details/44832831
AC代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
const int MAXN = 110;
const double INF = 0xffffffffffff;
const double eps = 1e-6;
struct Node
{
double x,y;
}Dot1[MAXN],Dot2[MAXN];
double Dist(Node a,Node b)
{
return -sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int N,NX,NY;
double Map[MAXN][MAXN];
int link[MAXN];
double lx[MAXN],ly[MAXN],slack[MAXN];
int visx[MAXN],visy[MAXN];
int FindPath(int u)
{
visx[u] = 1;
for(int i = 1; i <= NY; ++i)
{
if(visy[i])
continue;
double temp = lx[u] + ly[i] - Map[u][i];
if(fabs(temp) <= eps)
{
visy[i] = 1;
if(link[i] == -1 || FindPath(link[i]))
{
link[i] = u;
return 1;
}
}
else
{
if(slack[i] > temp)
slack[i] = temp;
}
}
return 0;
}
void KM()
{
memset(lx,0,sizeof(lx));
memset(ly,0,sizeof(ly));
memset(link,-1,sizeof(link));
for(int i = 1; i <= NX; ++i)
for(int j = 1; j <= NY; ++j)
if(Map[i][j] > lx[i])
lx[i] = Map[i][j];
for(int i = 1; i <= NX; ++i)
{
for(int j = 1; j <= NY; ++j)
slack[j] = INF;
while(1)
{
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(FindPath(i))
break;
double d = INF;
for(int j = 1; j <= NY; ++j)
if(!visy[j] && d > slack[j])
d = slack[j];
for(int j = 1; j <= NX; ++j)
if(visx[j])
lx[j] -= d;
for(int j = 1; j <= NY; ++j)
{
if(visy[j])
ly[j] += d;
else
slack[j] -= d;
}
}
}
}
int main()
{
int N;
while(~scanf("%d",&N))
{
memset(Map,0,sizeof(Map));
for(int i = 1; i <= N; ++i)
scanf("%lf%lf",&Dot1[i].x,&Dot1[i].y);
for(int i = 1; i <= N; ++i)
scanf("%lf%lf",&Dot2[i].x,&Dot2[i].y);
for(int i = 1; i <= N; ++i)
for(int j = 1; j <= N; ++j)
Map[i][j] = Dist(Dot1[i],Dot2[j]);
NX = NY = N;
KM();
for(int i = 1; i <= N; ++i)
{
for(int j = 1; j <= N; ++j)
{
if(link[j] == i)
{
printf("%d\n",j);
break;
}
}
}
}
return 0;
}