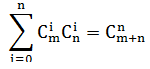2016"百度之星" - 初赛（Astar Round2B）解题报告
此文章可以使用目录功能哟↑(点击上方[+])
被自己蠢哭,去年还能进一下复赛,今年复赛都没戏了...
链接→2016"百度之星" - 初赛（Astar Round2B）
Problem 1001 区间的价值
Accept: 0 Submit: 0
Time Limit: 10000/5000 mSec(Java/Others) Memory Limit : 65536 KB
Problem Description
Input
Output
Sample Input
1 6 2 4 4
Sample Output
16
12
12
6
Problem Idea
解题思路:首先,我们可以用RMQ(理论上来说线段树也是可以的,查询O(logn),n次正好为O(nlogn),而ST算法预处理O(nlogn),查询O(1))预处理O(nlogn)出区间最大值,然后枚举区间的最小值点
为了枚举最小值点,我们需要知道每一个点作为最小值点左右可以延伸的最大范围l[i],r[i],求这两个数组可以用dp来做
预处理完之后,枚举最小值点,更新长度为r[i]-l[i]+1的区间的答案
枚举完之后,我们得到了一组值,但这并不是最后的答案
这是因为我们发现假如有一个最优区间,我们一定可以正好处理到或者处理到比这个区间小的区间,也就是说我们求的区间最大的值具有向下的包含性
举例来说,假如当前处理的区间为l[i],r[i],得到了答案ans,那么任何长度小于等于r[l]-l[I]+1的区间的答案都至少为ans
所以我们再用线性的时间递推求出答案即可
题目链接→HDU 5696 区间的价值
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 100005;
const int M = 40;
const int inf = 100000000;
const int mod = 2009;
int s[N],n,maxnum[N][20],l[N],r[N];
__int64 ans[N];
void RMQ() //预处理 O(nlogn)
{
int i,j;
int m=(int)(log(n*1.0)/log(2.0));
for(i=1;i<=n;i++)
maxnum[i][0]=s[i];
for(j=1;j<=m;j++)
for(i=1;i+(1<<j)-1<=n;i++)
maxnum[i][j]=max(maxnum[i][j-1],maxnum[i+(1<<(j-1))][j-1]);
}
int Ask_MAX (int a,int b) //O(1)
{
int k=int(log(b-a+1.0)/log(2.0));
return max(maxnum[a][k],maxnum[b-(1<<k)+1][k]);
}
int main()
{
int i,k;
while(~scanf("%d",&n))
{
memset(ans,0,sizeof(ans));
for(i=1;i<=n;i++)
{
scanf("%d",&s[i]);
l[i]=r[i]=i;
}
RMQ();
for(i=2;i<=n;i++)
{
k=i-1;
while(s[i]<=s[k])
k=l[k]-1;
l[i]=k+1;
}
for(i=n-1;i>0;i--)
{
k=i+1;
while(s[i]<=s[k])
k=r[k]+1;
r[i]=k-1;
}
for(i=1;i<=n;i++)
ans[r[i]-l[i]+1]=max(ans[r[i]-l[i]+1],(__int64)Ask_MAX(l[i],r[i])*s[i]);
for(i=n-1;i>0;i--)
ans[i]=max(ans[i+1],ans[i]);
for(i=1;i<=n;i++)
printf("%I64d\n",ans[i]);
}
return 0;
}
Problem 1003 瞬间移动
Accept: 0 Submit: 0
Time Limit: 4000/2000 mSec(Java/Others) Memory Limit : 65536 KB
Problem Description
有一个无限大的矩形，初始时你在左上角（即第一行第一列），每次你都可以选择一个右下方格子，并瞬移过去（如从下图中的红色格子能直接瞬移到蓝色格子），求到第n行第m列的格子有几种方案，答案对1000000007取模。
Input
多组测试数据。
Output
一个整数表示答案
Sample Input
Sample Output
Problem Idea
解题思路:除去起点(1,1)和终点(n,m)已经固定,中间能经过的是一个(n-2)*(m-2)的矩阵
然后我们可以在这个矩阵里取0个(就是直接从起点跳到终点)、1个、2个……min(n,m)-2个间接点
而对于取i个间接点,其实就是确定这i个间接点行数与列数有多少种取法
于是,我们得到了组合数公式(假设n<m,此题n,m和m,n结果是一样的,过我们可以交换n,m实现n<m)
组合数的求解我们可以交给Lucas定理,但是这个公式,我们还需要化简,不然计算100000项的组合数还是会超时
为了让式子看起来更简洁,对于输入的n与m,我们预处理-2,即n-=2,m-=2,这样上述式子就变成了
化简
剩下的就是套Lucas模板了,嫌时间长的还可以进行阶乘预处理
题目链接→HDU 5698 瞬间移动
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 100005;
const int M = 100;
const int inf = 1600000000;
const int p = 1000000007;
typedef long long LL;
LL quick_mod(LL a, LL b)
{
LL ans = 1;
a %= p;
while(b)
{
if(b & 1)
{
ans = ans * a % p;
b--;
}
b >>= 1;
a = a * a % p;
}
return ans;
}
LL C(LL n, LL m)
{
if(m > n) return 0;
LL ans = 1;
for(int i=1; i<=m; i++)
{
LL a = (n + i - m) % p;
LL b = i % p;
ans = ans * (a * quick_mod(b, p-2) % p) % p;
}
return ans;
}
LL Lucas(LL n, LL m)
{
if(m == 0) return 1;
return C(n % p, m % p) * Lucas(n / p, m / p) % p;
}
int main()
{
__int64 n,m;
int i;
while(~scanf("%I64d%I64d",&n,&m))
{
n-=2,m-=2;
if(n>m)
swap(n,m);
printf("%I64d\n",Lucas(m+n,n));
}
return 0;
}
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 200005;
const int M = 40;
const int inf = 100000000;
const int mod = 1000000007;
__int64 fac[N];
void init()//阶乘预处理
{
fac[0]=1;
for(int i=1;i<=N;i++)
fac[i]=i*fac[i-1]%mod;
}
__int64 pow_mod(__int64 a,__int64 b)
{
__int64 s=1;
a=a%mod;
while(b)
{
if(b&1)
s=s*a%mod;
a=a*a%mod;
b>>=1;
}
return s;
}
__int64 C(int n,int m)
{
if(n==0||m==0)
return 1;
return fac[n]*pow_mod(fac[m]*fac[n-m]%mod,mod-2)%mod;
}
int main()
{
int n,m;
init();
while(~scanf("%d%d",&n,&m))
{
n-=2;m-=2;
printf("%I64d\n",C(m+n,min(n,m))%mod);
}
return 0;
}
Problem 1005 区间交
Accept: 0 Submit: 0
Time Limit: 8000/4000 mSec(Java/Others) Memory Limit : 65536 KB
Problem Description
Input
Output
一行表示答案
Sample Input
1 2 3 4 6
4 5
2 5
1 4
Sample Output
Problem Idea
解题思路:此题的做法有很多种,不过有种利用STL来解的做法,我觉得挺巧妙的
首先利用vector将区间分组,将所有具有公共左端点的区间划分成一组,比如[3,7],[3,11],[3,4]等,这些都是一组的
接下来就是利用multiset来进行模拟了(顺带提一句,这里不能用set,而用multiset,是因为set无法存储重复相同的数)
对于当前所在位置i,将所有以i作为左端点的区间右端点值插入multiset(multiset内的数默认从小到大排列)中
若multiset的大小超过了k,那我就删除multiset内最小的值直到小于等于k(之所以删除最小的值,是因为在左端点固定的情况下,右端点越小,会使得区间交的位置数越少)
当且仅当multiset大小恰好等于k,且multiset中当前最小的右端点值≥i时,我们找到了一种符合题目要求的区间取法,于是我们更新答案
当然,在开始的时候,我们需要预处理前n项和sum[n]
题目链接→HDU 5700 区间交
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 100005;
const int M = 10;
const int inf = 1600000000;
const int mod = 2009;
__int64 sum[N],ans;
multiset<int> s;
vector<int> v[N];
int main()
{
int n,k,m,i,j,l,r;
while(~scanf("%d%d%d",&n,&k,&m))
{
s.clear();ans=0;
for(i=1;i<=n;i++)
{
scanf("%I64d",&sum[i]);
sum[i]+=sum[i-1];
v[i].clear();
}
for(i=0;i<m;i++)
{
scanf("%d%d",&l,&r);
v[l].push_back(r);
}
for(i=1;i<=n;i++)
{
for(j=0;j<v[i].size();j++)
s.insert(v[i][j]);
while(s.size()>k)
s.erase(s.begin());
if(s.size()==k&&*s.begin()>=i)
ans=max(ans,sum[*s.begin()]-sum[i-1]);
}
printf("%I64d\n",ans);
}
return 0;
}
Problem 1006 中位数计数
Accept: 0 Submit: 0
Time Limit: 12000/6000 mSec(Java/Others) Memory Limit : 65536 KB
Problem Description
中位数定义为所有值从小到大排序后排在正中间的那个数，如果值有偶数个，通常取最中间的两个数值的平均数作为中位数。
现在有n个数，每个数都是独一无二的，求出每个数在多少个包含其的区间中是中位数。
Input
第一行一个数n(n≤8000)
第二行n个数，0≤每个数≤
Output
N个数，依次表示第i个数在多少包含其的区间中是中位数。
Sample Input
1 2 3 4 5
Sample Output
Problem Idea
解题思路:很显然,此题O(n^2logn)的暴力做法必然会TLE,所以我们要想办法做到O(n^2)的复杂度
首先对于第i个数,我们从i-1个数开始递减,分别与第i个数进行比较,假设比第i个数大的数的个数即为l,比第i个数小的数的个数即为r,dp[l-r=k]则为[比第i个数大的数的个数]比[比第i个数小的数的个数]多k个的区间个数,那要保证第i个数是区间内的中位数,我只需要在第i个数的右边找有多少个[比第i个数小的数的个数]比[比第i个数大的数的个数]多k个的区间,这样两个区间连接起来,正好[比第i个数大的数的个数]与[比第i个数小的数的个数]一样多,这样,第i个数就是此区间内的中位数
另外,因为数组下标必须为非负整数,故把数组的中心点移至8000,即dp[8000+k],这样就保证了下标一定是符合要求的
题目链接→HDU 5701 中位数计数
Source Code
/*Sherlock and Watson and Adler*/
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define exp 1e-10
using namespace std;
const int N = 8005;
const int M = 8000;
const int inf = 100000000;
const int mod = 1000000007;
int s[N],dp[2*N];
int main()
{
int n,i,j,k,ans;
while(~scanf("%d",&n))
{
for(i=0;i<n;i++)
scanf("%d",&s[i]);
for(i=0;i<n;i++)
{
memset(dp,0,sizeof(dp));
dp[M]=1;
for(k=0,j=i-1;j>=0;j--)
{
if(s[j]>s[i])
k++;
else
k--;
dp[M+k]++;
}
for(ans=dp[M],k=0,j=i+1;j<n;j++)
{
if(s[j]>s[i])
k++;
else
k--;
ans+=dp[M-k];
}
printf("%d%c",ans,i!=n-1?' ':'\n');
}
}
return 0;
}
菜鸟成长记