华为机试之广度优先遍历

在华为的论坛上看到了下面这个题目，想着最近刚好没事，就来写一下。

编译环境：VS2005

高级题：地铁换乘

已知2条地铁线路，其中A为环线，B为东西向线路，线路都是双向的。经过的站点名分别如下，两条线交叉的换乘点用T1、T2表示。编写程序，任意输入两个站点名称，输出乘坐地铁最少需要经过的车站数量（含输入的起点和终点，换乘站点只计算一次）。
地铁线A（环线）经过车站：A1 A2 A3 A4 A5 A6 A7 A8 A9 T1 A10 A11 A12 A13 T2 A14 A15 A16 A17 A18
地铁线A（直线）经过车站：B1 B2 B3 B4 B5 T1 B6 B7 B8 B9 B10 T2 B11 B12 B13 B14 B15

输入：输入两个不同的站名

输出：输出最少经过的站数,含输入的起点和终点，换乘站点只计算一次

刚开始看到这道题的时候，感觉是用链表，但具体怎么写不会

参考了别人的程序，具体思路是先用邻接表建立无向图，然后广度优先遍历

之前学数据结构的时候，只是明确了排序、链表、查找、图等基本概念，具体如何用程序实现则没有涉及

这里有2个基本数据结构，边表edgenode和顶点表vernode

顶点表指各链表的第一个

链表中除第一个其他是边表

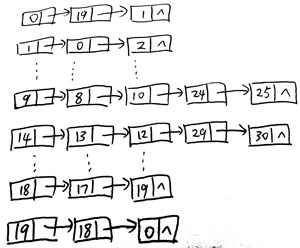
左图为环线A线，右图为直线B线，其中9为换乘站T1，14为换乘站T2

广度优先遍历：

这里我们需要用到队列queue，需要include<queue>

1.指定起点A2和终点A4

2.若顶点A2不在队列中，则将顶点A2压入队列

3.将顶点A2弹出队列前，先检查该顶点A2是不是终点，若是，则break；若不是，则将该顶点A2的下一层的顶点（A3和A1）压入队列，然后把该顶点A2弹出队列。当将下一层的顶点压入队列时，计数值加1，这样我们就可以得到下一层该检查的顶点数（在此例中是2）

4.检查该层的顶点是否都检查完，若没检查完，则继续第3步；若检查完了，则开始下一层的检查

下图为简易思路：

下面给出实现代码：

#include <vector>
#include <iostream>
#include <conio.h>
#include <string.h>
#include <queue>
using namespace std;

#define MAX 35 
#define SUBWAY_A 20
#define SUBWAY_B 15

typedef struct node{//边表
	int  adjvex;
	struct node *next;
}edgenode;

typedef struct{//顶点表
	int data;
	edgenode *first;
	char name[5];
	char visit_flag;
}vernode;

const char subway_name1[SUBWAY_A][5]={"A1","A2","A3","A4","A5","A6","A7","A8","A9","T1","A10","A11","A12","A13","T2","A14",
"A15","A16","A17","A18"};
const char subway_name2[SUBWAY_B][5]={"B1","B2","B3","B4","B5","B6","B7","B8","B9","B10","B11","B12","B13","B14","B15"};
vernode ga[MAX];
/*
函数输入：vernode ga[]顶点表
函数输出：无
函数功能：用邻接表表示图
*/
void creat(vernode ga[])
{
	edgenode *p; 

	//初始化
	for(int i=0;i<MAX;i++)
	{
		ga[i].first = NULL;
		ga[i].visit_flag = 0;//未入列
		if(i<=19)
			strcpy(ga[i].name,subway_name1[i]);
		else
			strcpy(ga[i].name,subway_name2[i-SUBWAY_A]);
	}

	//建立A地铁图
	for(int i=1;i<=SUBWAY_A-2;i++)
	{	
		ga[i].data = i;

		p = (edgenode*)malloc(sizeof(edgenode));
		p->adjvex = i-1;
		p->next = ga[i].first;
		ga[i].first = p;

		p = (edgenode*)malloc(sizeof(edgenode));
		p->adjvex = i+1;
		p->next = ga[i].first;
		ga[i].first = p;
	}
	//0顶点
	ga[0].data = 0;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 19;
	p->next = ga[0].first;
	ga[0].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 1;
	p->next = ga[0].first;
	ga[0].first = p;

	//19顶点
	ga[19].data = 19;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 18;
	p->next = ga[19].first;
	ga[19].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 0;
	p->next = ga[19].first;
	ga[19].first = p;

	//9 T1换乘站
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 24;
	p->next = ga[9].first;
	ga[9].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 25;
	p->next = ga[9].first;
	ga[9].first = p;

	//14 T2换乘站
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 29;
	p->next = ga[14].first;
	ga[14].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 30;
	p->next = ga[14].first;
	ga[14].first = p;


	//建立B地铁图
	for(int i=1+SUBWAY_A;i<=33;i++)
	{	
		if((i==24)|(i==25)|(i==29)|(i==30))continue;

		ga[i].data = i;

		p = (edgenode*)malloc(sizeof(edgenode));
		p->adjvex = i-1;
		p->next = ga[i].first;
		ga[i].first = p;

		p = (edgenode*)malloc(sizeof(edgenode));
		p->adjvex = i+1;
		p->next = ga[i].first;
		ga[i].first = p;
	}

	//24顶点连接9 T1
	ga[24].data = 24;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 23;
	p->next = ga[24].first;
	ga[24].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 9;
	p->next = ga[24].first;
	ga[24].first = p;

	//25顶点连接9 T1
	ga[25].data = 25;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 26;
	p->next = ga[25].first;
	ga[25].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 9;
	p->next = ga[25].first;
	ga[25].first = p;

	//29顶点连接14 T2
	ga[29].data = 29;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 28;
	p->next = ga[29].first;
	ga[29].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 14;
	p->next = ga[29].first;
	ga[29].first = p;

	//30顶点连接14 T2
	ga[30].data = 30;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 31;
	p->next = ga[30].first;
	ga[30].first = p;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 14;
	p->next = ga[30].first;
	ga[30].first = p;

	//20端点连接21
	ga[20].data = 20;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 21;
	p->next = ga[20].first;
	ga[20].first = p;

	//34端点连接33
	ga[34].data = 34;
	p = (edgenode*)malloc(sizeof(edgenode));
	p->adjvex = 33;
	p->next = ga[34].first;
	ga[34].first = p;

	edgenode *s;

	//打印显示线路图
	for(int i=0;i<MAX;i++)
	{
	//	cout << ga[i].data;
		cout << ga[i].name;
		s = ga[i].first;
		while(s!=NULL)
		{
			cout << "->" << ga[s->adjvex].name;
			s = s->next;
		}
		cout << endl;
	}
}
/*
函数功能：对建立好的图进行广度优先遍历
函数输入输出：无
*/
void Get_SUBWAY_LINE()
{
	char str[2][5];
	int start_i;
	cout <<"*************************************\n请输入起点与终点：";
	while(scanf("%s %s",str[0],str[1])!=EOF)//输入两个站
	{
		
		char find_flag = 0;
		int count=0,num=0,temp_num=1;
		edgenode *s;
		queue<vernode>q;
		for(int i=0;i<MAX;i++)
		{
			ga[i].visit_flag = 0;//未入列
		}

		for(int i=0;i<MAX;i++)
			if(!strcmp(str[0],ga[i].name))
			{
				start_i = i;
				break;
			}

		if(!ga[start_i].visit_flag)//未入列则入列
		{
			q.push(ga[start_i]);
			ga[start_i].visit_flag = 1;
		}

		while(!q.empty())//寻找路径
		{
			if(find_flag)
			{
				cout << "共需经过"<<count<<"站\n*************************************\n\n";
				cout <<"*************************************\n请输入起点与终点：";
				break;//找到路径
			}
			count++;
			cout << "****第" << count <<"次搜索****"<<endl;
			for(int i=0;i<temp_num;i++)//取出同一层的各站点比对
			{
				//查看队列头是否为终点，若是，break
				cout << q.front().name<<"  ";
				if(!strcmp(str[1],q.front().name))//找到终点站
				{
					find_flag = 1;
					break;
				}

				//队列头若不是终点，将它的下一层加入到队列中，并将它弹出
				s = q.front().first;
				while(s!=NULL)//将下一层的广度都送入队列
				{
					if(!ga[s->adjvex].visit_flag)
					{	
						q.push(ga[s->adjvex]);
						num++;
						ga[s->adjvex].visit_flag = 1;
					}
					s = s->next;
				}
				q.pop();
			}//for
			temp_num = num;
			num = 0;
			cout << endl;

		}//while(!q.empty())

	}//while

}
void main()
{
	creat(ga);
	Get_SUBWAY_LINE();
}