在unity向量空间内绘制几何(2)：球面---重构《黑客帝国》的‘上帝机器’，Deus Ex Machina

上一篇文章：在unity向量空间内通过将极坐标转换为直角坐标，绘制阿基米德螺线，对数螺线与玫瑰线等几何图形

今天进一步研究一下如何获取一个球面的三维坐标。
视频地址：http://v.youku.com/v_show/id_XMTU5MTI5OTU0OA==.html

在电影黑客帝国第三部分矩阵革命的最后部分，有一段NEO独创机器城与机器世界的首领交涉的情节。

这个机器首领的名字叫做Deus Ex Machina，拉丁文翻译成英文是God out of the machine，是机器城市的中枢，控制着所有机器。

下文将会尝试在Unity向量空间内，通过将球面的极坐标公式转化成代码模拟重构这个‘上帝机器’。

这个是做好的效果的视频地址：http://v.youku.com/v_show/id_XMTU5MTI5OTU0OA==.html

首先先了解三维空间内的球面的极坐标公式，假如有以下三维空间坐标系（见图片）：

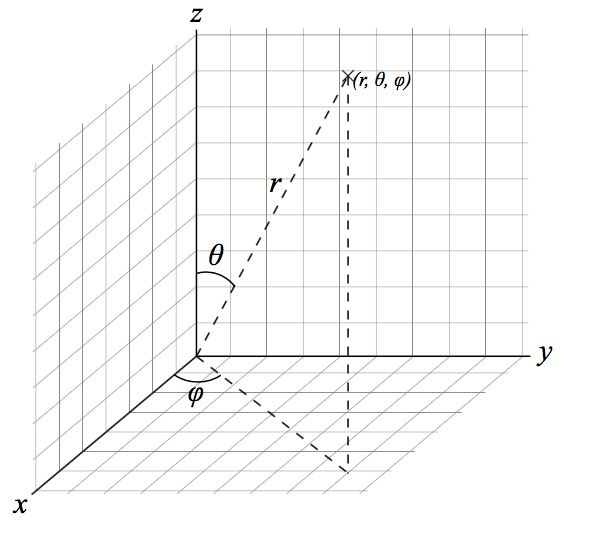
那么，球面sphere上的任意一点的三维坐标x,y,z,可以用以下极坐标公式表示：
x=r∗sinθ∗cosϕ
y=r∗sinθ∗sinϕ
y=r∗cosθ
(公式-1)

现在把公式转换为C#代码：

    public Vector3[] GenerateSSphereVectro3(int radius,Vector3 centre,int thetaPortion,int phiPortion){

        Vector3[] coordinates=new Vector3[thetaPortion*phiPortion];

        float thetaMultiplier=360f/(float)thetaPortion;
        float phiMultiplier=360f/(float)phiPortion;

        for(int i=0,index=0;i<thetaPortion;i++){
            for(int j=0;j<phiPortion;j++){
                coordinates[index]=new Vector3(radius*Mathf.Sin(i*thetaMultiplier)*Mathf.Cos(j*phiMultiplier),radius*Mathf.Sin(i*thetaMultiplier)*Mathf.Sin(j*phiMultiplier),radius*Mathf.Cos(i*thetaMultiplier));
                index+=1;
            }
        }

        return coordinates;
    }

解析代码：
方法参数：
int radius:球体半径。
Vector3 centre:球体圆心。
int thetaPortion:将 θ 角平均分成的份数。
int phiPortion:将 ϕ 角平均分成的份数。
返回值：
Vector3 coordinates:一组分布在球面的三维坐标向量。数量为thetaPortion*phiPortion个。

方法内容解析：
1，根据传进的thetaPortion与phiPortion参数声明一组三维坐标数组

Vector3[] coordinates=new Vector3[thetaPortion*phiPortion];

2,根据传进的thetaPortion与phiPortion参数计算坐标点在极坐标公式中相差的角度。

float thetaMultiplier=360f/(float)thetaPortion;
float phiMultiplier=360f/(float)phiPortion;

3，通过两个for循环，依次寻找球面上的每个坐标点。

for(int i=0,index=0;i<thetaPortion;i++){
            for(int j=0;j<phiPortion;j++){
                coordinates[index]=new Vector3(radius*Mathf.Sin(i*thetaMultiplier)*Mathf.Cos(j*phiMultiplier),radius*Mathf.Sin(i*thetaMultiplier)*Mathf.Sin(j*phiMultiplier),radius*Mathf.Cos(i*thetaMultiplier));
                index+=1;
            }
        }

这就是将球面的极坐标公式转换为C#代码的主要部分。

接下来，生成一个锥形体，并选择一个内发光的shader。

Unity自带的几何模型中没有圆锥体。以下是生成圆锥体的代码，并非我原创，源码地址http://wiki.unity3d.com/index.php?title=CreateCone，作者Wolfram Kresse。将此脚本放在/Assets/Editor 文件夹下。然后上方菜单的GameObject/CreatOther里会出现cone。

using UnityEngine;
using UnityEditor;
using System.Collections;

// an Editor method to create a cone primitive (so far no end caps)
// the top center is placed at (0/0/0)
// the bottom center is placed at (0/0/length)
// if either one of the radii is 0, the result will be a cone, otherwise a truncated cone
// note you will get inevitable breaks in the smooth shading at cone tips
// note the resulting mesh will be created as an asset in Assets/Editor
// Author: Wolfram Kresse
public class CreateCone : ScriptableWizard {

    public int numVertices = 10;
    public float radiusTop = 0f;
    public float radiusBottom = 1f;
    public float length = 1f;
    public float openingAngle = 0f; // if >0, create a cone with this angle by setting radiusTop to 0, and adjust radiusBottom according to length;
    public bool outside = true;
    public bool inside = false;
    public bool addCollider = false;

    [MenuItem ("GameObject/Create Other/Cone")]
    static void CreateWizard()
    {
        ScriptableWizard.DisplayWizard("Create Cone", typeof(CreateCone));
    }

    void OnWizardCreate(){
        GameObject newCone=new GameObject("Cone");
        if(openingAngle>0&&openingAngle<180){
            radiusTop=0;
            radiusBottom=length*Mathf.Tan(openingAngle*Mathf.Deg2Rad/2);
        }
        string meshName = newCone.name + numVertices + "v" + radiusTop + "t" + radiusBottom + "b" + length + "l" + length + (outside?"o":"") + (inside?"i":"");
        string meshPrefabPath = "Assets/Editor/" + meshName + ".asset";
        Mesh mesh = (Mesh)AssetDatabase.LoadAssetAtPath(meshPrefabPath, typeof(Mesh));
        if(mesh==null){
            mesh=new Mesh();
            mesh.name=meshName;
            // can't access Camera.current
            //newCone.transform.position = Camera.current.transform.position + Camera.current.transform.forward * 5.0f;
            int multiplier=(outside?1:0)+(inside?1:0);
            int offset=(outside&&inside?2*numVertices:0);
            Vector3[] vertices=new Vector3[2*multiplier*numVertices]; // 0..n-1: top, n..2n-1: bottom
            Vector3[] normals=new Vector3[2*multiplier*numVertices];
            Vector2[] uvs=new Vector2[2*multiplier*numVertices];
            int[] tris;
            float slope=Mathf.Atan((radiusBottom-radiusTop)/length); // (rad difference)/height
            float slopeSin=Mathf.Sin(slope);
            float slopeCos=Mathf.Cos(slope);
            int i;

            for(i=0;i<numVertices;i++){
                float angle=2*Mathf.PI*i/numVertices;
                float angleSin=Mathf.Sin(angle);
                float angleCos=Mathf.Cos(angle);
                float angleHalf=2*Mathf.PI*(i+0.5f)/numVertices; // for degenerated normals at cone tips
                float angleHalfSin=Mathf.Sin(angleHalf);
                float angleHalfCos=Mathf.Cos(angleHalf);

                vertices[i]=new Vector3(radiusTop*angleCos,radiusTop*angleSin,0);
                vertices[i+numVertices]=new Vector3(radiusBottom*angleCos,radiusBottom*angleSin,length);

                if(radiusTop==0)
                    normals[i]=new Vector3(angleHalfCos*slopeCos,angleHalfSin*slopeCos,-slopeSin);
                else
                    normals[i]=new Vector3(angleCos*slopeCos,angleSin*slopeCos,-slopeSin);
                if(radiusBottom==0)
                    normals[i+numVertices]=new Vector3(angleHalfCos*slopeCos,angleHalfSin*slopeCos,-slopeSin);
                else
                    normals[i+numVertices]=new Vector3(angleCos*slopeCos,angleSin*slopeCos,-slopeSin);

                uvs[i]=new Vector2(1.0f*i/numVertices,1);
                uvs[i+numVertices]=new Vector2(1.0f*i/numVertices,0);

                if(outside&&inside){
                    // vertices and uvs are identical on inside and outside, so just copy
                    vertices[i+2*numVertices]=vertices[i];
                    vertices[i+3*numVertices]=vertices[i+numVertices];
                    uvs[i+2*numVertices]=uvs[i];
                    uvs[i+3*numVertices]=uvs[i+numVertices];
                }
                if(inside){
                    // invert normals
                    normals[i+offset]=-normals[i];
                    normals[i+numVertices+offset]=-normals[i+numVertices];
                }
            }
            mesh.vertices = vertices;
            mesh.normals = normals;     
            mesh.uv = uvs;

            // create triangles
            // here we need to take care of point order, depending on inside and outside
            int cnt=0;
            if(radiusTop==0){
                // top cone
                tris=new int[numVertices*3*multiplier];
                if(outside)
                    for(i=0;i<numVertices;i++){
                        tris[cnt++]=i+numVertices;
                        tris[cnt++]=i;
                        if(i==numVertices-1)
                            tris[cnt++]=numVertices;
                        else
                            tris[cnt++]=i+1+numVertices;
                    }
                if(inside)
                    for(i=offset;i<numVertices+offset;i++){
                        tris[cnt++]=i;
                        tris[cnt++]=i+numVertices;
                        if(i==numVertices-1+offset)
                            tris[cnt++]=numVertices+offset;
                        else
                            tris[cnt++]=i+1+numVertices;
                    }
            }else if(radiusBottom==0){
                // bottom cone
                tris=new int[numVertices*3*multiplier];
                if(outside)
                    for(i=0;i<numVertices;i++){
                        tris[cnt++]=i;
                        if(i==numVertices-1)
                            tris[cnt++]=0;
                        else
                            tris[cnt++]=i+1;
                        tris[cnt++]=i+numVertices;
                    }
                if(inside)
                    for(i=offset;i<numVertices+offset;i++){
                        if(i==numVertices-1+offset)
                            tris[cnt++]=offset;
                        else
                            tris[cnt++]=i+1;
                        tris[cnt++]=i;
                        tris[cnt++]=i+numVertices;
                    }
            }else{
                // truncated cone
                tris=new int[numVertices*6*multiplier];
                if(outside)
                    for(i=0;i<numVertices;i++){
                        int ip1=i+1;
                        if(ip1==numVertices)
                            ip1=0;

                        tris[cnt++]=i;
                        tris[cnt++]=ip1;
                        tris[cnt++]=i+numVertices;

                        tris[cnt++]=ip1+numVertices;
                        tris[cnt++]=i+numVertices;
                        tris[cnt++]=ip1;
                    }
                if(inside)
                    for(i=offset;i<numVertices+offset;i++){
                        int ip1=i+1;
                        if(ip1==numVertices+offset)
                            ip1=offset;

                        tris[cnt++]=ip1;
                        tris[cnt++]=i;
                        tris[cnt++]=i+numVertices;

                        tris[cnt++]=i+numVertices;
                        tris[cnt++]=ip1+numVertices;
                        tris[cnt++]=ip1;
                    }
            }
            mesh.triangles = tris;      
            AssetDatabase.CreateAsset(mesh, meshPrefabPath);
            AssetDatabase.SaveAssets();
        }

        MeshFilter mf=newCone.AddComponent<MeshFilter>();
        mf.mesh = mesh;

        newCone.AddComponent<MeshRenderer>();

        if(addCollider){
            MeshCollider mc=newCone.AddComponent<MeshCollider>();
            mc.sharedMesh=mf.sharedMesh;
        }

        Selection.activeObject = newCone;
    }
}

接着实例化thetaPortion*phiPortion个圆锥体，把球面的三维坐标依次赋值给它们的position，调整角度，为了达成动画效果，构造一些空物体作为圆锥体们的父物体。并在Update里面让父物体们进行旋转。

        if(rotateFlag){
            for(int i=0;i<thetaPortion;){
                parents[i].transform.Rotate(Vector3.forward,rotateSpeed);
                i+=2;
            }
            for(int i=1;i<thetaPortion;){
                parents[i].transform.Rotate(Vector3.back,rotateSpeed);
                i+=2;
            }
        }

立方体版本

圆锥体版本

放进去一些雷电的特效，闪电的中心点在圆心，闪电的终点随机寻找各个圆锥体的尖部。这个闪电效果在AssetStore内名为Procedural Examples，可以免费下载。

    IEnumerator lightingMove(){
        for(int i=0;i<100;i++){
            for(int j=0;j<21;j++){
                lightingEmitters[j].transform.position=Ball[Random.Range(0,1296)];
                yield return new WaitForSeconds(0.2f);
            }
        }
    }

加些音效，利用DoTween写个摄像机移动路径，录制视频，完成。

    private Vector3[] circlePoints=new Vector3[200];
    // Use this for initialization
    void Start () {
        for(int i=0;i<200;i++){
            circlePoints=Circle(200,18,new Vector3(0f,5f,0f));
        }
        transform.position=circlePoints[0];
        transform.DOPath(circlePoints,130f);
    }

    // Update is called once per frame
    void Update () {
        transform.LookAt(Vector3.zero);
    }

视频地址：http://v.youku.com/v_show/id_XMTU5MTI5OTU0OA==.html