决策树介绍一

决策树(Decision tree)是一种基本的分类与回归方法,尤其是在各大竞赛中,很多最后胜出的算法都是树模型组合起来的.决策树的学习通常分为三部分:特征选择,决策树的生成和决策树的剪枝.本文主要介绍决策树学习的ID3,C4.5算法,C5.0算法和CART 树.为了更好的理解本文,请先阅读信息论基础.

1 例子

决策树可以理解成是很多 if−then if−then的规则组合.下图就是一棵典型的决策树:

这棵决策树根据天气情况分类“星期六上午是否适合打网球”,根节点到叶节点的每一条路径构成了一条规则,路径上的内部节点对应规则的条件,叶节点的类对应着规则的结论.

• 规则1:如果晴天,湿度很高就不去打网球
• 规则2:如果晴天,湿度一般就去打网球
• 规则3:如果是阴天,就去打网球
• 规则4:如果是雨天,而且大风,就不去打网球
• 规则5:如果是雨天,但是微风,就去打网球

再比如,某位母亲给自己闺女物色了个男朋友,于有了下面这段对话:

• 女儿:多大年纪了?
• 母亲:26.
• 女儿:长得帅不帅?
• 母亲:挺帅的.
• 女儿:收入高不?
• 母亲:不算特别高,中等情况吧.
• 女儿:是不是公务员?
• 母亲:是,在税务局上班.
• 女儿:那好,见个面吧.

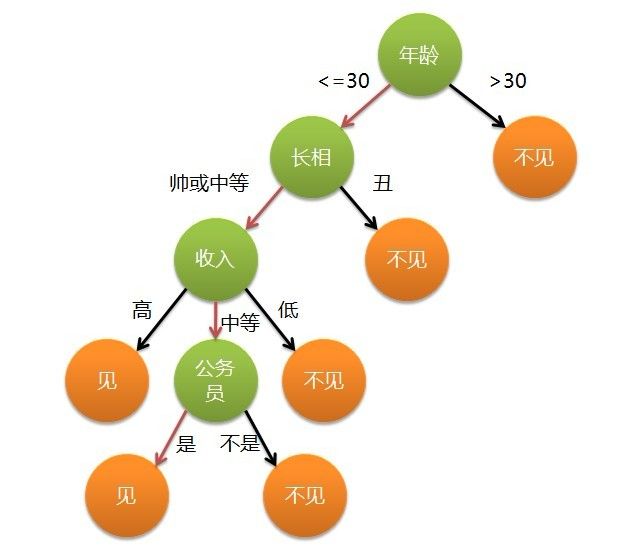
这个女孩的决策过程就是典型的分类决策过程.相当于通过年龄,长相,收入和是否是公务员将男人分成两类:见和不见.假设这个女孩对男人的要求是:30岁以下,长相中等,高收入或者中等收入的公务员,那么可以用下图来表示女孩的决策逻辑:

下面就以一个例子来说明决策树学习的各种算法.
我们希望能够学习出一个贷款申请的决策树,当新的客户提出申请贷款时,根据申请人的特征利用决策树决定是否批准申请贷款.

ID	年龄	有工作	有自己的房子	信贷情况	类别
1	青年	否	否	一般	否
2	青年	否	否	好	否
3	青年	是	否	好	是
4	青年	是	是	一般	是
5	青年	否	否	一般	否
6	中年	否	否	一般	否
7	中年	否	否	好	否
8	中年	是	是	好	是
9	中年	否	是	非常好	是
10	中年	否	是	非常好	是
11	老年	否	是	非常好	是
12	老年	否	是	好	是
13	老年	是	否	好	是
14	老年	是	否	非常好	是
15	老年	否	否	一般	否

这个例子中,我们有年龄,工作,房子,信贷情况等特征:

年龄	青年,中年,老年
工作	是,否
房子	是,否
信贷情况	一般,好,非常好

如果我们根据这些条件逐步去构建决策树的话,如何选择每个节点呢? 比如我们的根节点是选年龄好还是选工作好? 不同的算法选择的标准不一样.在了解这些算法之前,请先阅读信息论基础这篇文章,确保理解了里面介绍到的概念.

2 ID3

ID3由Ross Quinlan于1986年提出.

它根据信息增益(Information gain)来选取Feature作为决策树分裂的节点.特征 A A对训练数据集 D D的信息增益定义为集合D的经验熵(所谓经验熵,指的是熵是有某个数据集合估计得到的) H(D) H(D)与特征 A A给定条件下 D D的经验条件熵  H(D∣A) H(D∣A) 之差,记为  g(D,A) g(D,A).

g(D,A)=H(D)−H(D|A) g(D,A)=H(D)−H(D|A)

实际上就是特征 A A和 D D的互信息.分别以 A1,A2,A3,A4 A1,A2,A3,A4 来表示年龄,工作,房子和信贷情况4个特征,下面来计算每个特征的信息增益.上面的例子,按照类别整理成表格如下:

类别	ID	数量
是	3,4,8,9,10,11,12,13,14	9
否	1,2,5,6,7,15	6

所以:

H(D)=−915log915−615log615=0.971 H(D)=−915log⁡915−615log⁡615=0.971

A1=青年 A1=青年时:

类别,年龄	青年	数量
是	3,4	2
否	1,2,5	3

H(D|A1=青年)=−25log25−35log35=0.971 H(D|A1=青年)=−25log⁡25−35log⁡35=0.971

A1=中年 A1=中年时:

类别,年龄	中年	数量
是	8,9,10	3
否	6,7	2

H(D|A1=中年)=−35log35−25log25=0.971 H(D|A1=中年)=−35log⁡35−25log⁡25=0.971

A1=老年 A1=老年时:

类别,年龄	老年	数量
是	7,8,9,10	4
否	15	1

H(D|A1=老年)=−45log45−15log15=0.722 H(D|A1=老年)=−45log⁡45−15log⁡15=0.722

所以:

H(D|A1)=515H(D|A1=青年)+515H(D|A1=中年)+515H(D|A1=老年)=515×0.971+515×0.971+515×0.722=0.888 H(D|A1)=515H(D|A1=青年)+515H(D|A1=中年)+515H(D|A1=老年)=515×0.971+515×0.971+515×0.722=0.888

由此可以计算出:

g(D,A1)=H(D)−H(D|A1)=0.971−0.888=0.083g(D,A2)=0.324g(D,A3)=0.420g(D,A4)=0.363 g(D,A1)=H(D)−H(D|A1)=0.971−0.888=0.083g(D,A2)=0.324g(D,A3)=0.420g(D,A4)=0.363

总结一下上面的计算过程,假设训练数据集为  D D, ∣D∣ ∣D∣表示其大小.设有  K K 个分类  C1,C2,…,Ck C1,C2,…,Ck, ∣Ck∣ ∣Ck∣为类  Ck Ck 的大小,即样本个数,  ∑Kk=1∣Ck∣=∣D∣ ∑k=1K∣Ck∣=∣D∣ .设特征  A A 有  n n 个不同的取值  {a1,a2,…,an} {a1,a2,…,an},根据特征  A A 的取值将  D D 划分成  n n 个子集  D1,D2,…,Dn D1,D2,…,Dn, ∣Di∣ ∣Di∣ 为  Di Di 的大小,  ∑ni=1∣Di∣ ∑i=1n∣Di∣ .记子集  Di Di中属于类  Ck Ck的样本集合为  Dik Dik,  ∣Dik∣ ∣Dik∣ 为  Dik Dik 的大小.于是信息增益的算法如下:

• 计算数据集  D D 的经验熵 H(D)

H(D)=−∑k=1K|Ck|Dlog|Ck|D H(D)=−∑k=1K|Ck|Dlog⁡|Ck|D

• 计算特征 A A对数据集  D D 的经验条件熵

H(D|A)=∑i=1nDiDH(Di)=−∑i=1n∑k=1K|Dik|Dilog|Dik|Di H(D|A)=∑i=1nDiDH(Di)=−∑i=1n∑k=1K|Dik|Dilog⁡|Dik|Di

ID3从根节点开始,计算所有可能特征的信息增益,取信息增益最大的特征作为节点的特征,然后由特征的不同取值,建立子节点,再对子节点递归调用以上方法,知道所有特征的信息增益都很小或者没有特征选择为止.

具体为:

1. 若 D D中所有实例都属于同一类  Ck Ck,则  T T 为单节点树,并将类  Ck Ck作为该节点的类标记,返回 T T.
2. 若 A=Φ A=Φ,则 T T为单节点树,并将 D D中实例最大的类 Ck Ck作为该节点的类标记,返回 T T.
3. 否则,按照信息增益的算法,计算每个特征对 D D的信息增益,取信息增益最大的特征  Ag Ag.
4. 如果  Ag<ε Ag<ε,则置  T T 为单节点树,并将 D D中实例最大的类 Ck Ck作为该节点的类标记,返回 T T.
5. 否则,对 Ag Ag的每一可能值  ai ai,依 Ag=ai Ag=ai将 D D分成若干非空子集 Di Di,将 Di Di中实例最大的类作为标记,构建子节点,由节点和子节点构成树 T T,返回 T T.
6. 对第  i i 个子节点,以 Di Di为训练集,以 A−{Ag} A−{Ag} 为特征集,递归地调用步骤1到步骤5,得到子树  Ti Ti,返回 Ti Ti.

3 C4.5

C4.5由Ross Quinlan于1993年提出.ID3采用的信息增益度量存在一个内在偏置,它优先选择有较多属性值的Feature,因为属性值多的Feature会有相对较大的信息增益?(信息增益反映的给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大).避免这个不足的一个度量就是不用信息增益来选择Feature,而是用信息增益比率(gain ratio),增益比率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的Feature,分裂信息用来衡量Feature分裂数据的广度和均匀性:

SplitInformation(D,A)=−∑i=1n|Di||D|log|Di||D| SplitInformation(D,A)=−∑i=1n|Di||D|log⁡|Di||D|

GainRatio(D,A)=g(D,A)SplitInformation(D,A) GainRatio(D,A)=g(D,A)SplitInformation(D,A)

但是当某个 Di Di的大小跟 D D的大小接近的时候, SplitInformation(D,A)→0,GainRatio(D,A)→∞ SplitInformation(D,A)→0,GainRatio(D,A)→∞,为了避免这样的属性,可以采用启发式的思路,只对那些信息增益比较高的属性才应用信息增益比率.

相比ID3,C4.5还能处理连续属性值,具体步骤为:

• 把需要处理的样本(对应根节点)或样本子集(对应子树)按照连续变量的大小从小到大进行排序.
• 假设该属性对应的不同的属性值一共有 N N个,那么总共有 N−1 N−1个可能的候选分割阈值点,每个候选的分割阈值点的值为上述排序后的属性值中两两前后连续元素的中点,根据这个分割点把原来连续的属性分成bool属性.实际上可以不用检查所有 N−1 N−1个分割点,具体请看下面的例子.
• 用信息增益比率选择最佳划分.

假设上面关于贷款的例子还有个属性是收入情况,对应的数据如下(已经排好序):

收入(百)	40	48	60	72	80	90
类别	否	否	是	是	是	否

可以证明这时候的切分点,只能出现在目标分类不同的相邻实例之间,即出现在(48,60)和(80,90)之间,这时候选取切分点  s1=(48+60)/2=54 s1=(48+60)/2=54 和  s2=(80+90)/2=85 s2=(80+90)/2=85.利用 s1=54 s1=54就可以将收入分成小于54和大于54两类.连续属性值比较多的时候,由于需要排序和扫描,会使C4.5的性能有所下降.

C4.5还能对缺失值进行处理,处理的方式通常有三种:

• 赋上该属性最常见的值
• 根据节点的样例上该属性值出现的情况赋一个概率,比如该节点上有10个样本,其中属性A的取值有6个为是,4个为否.那么对改节点上缺失的属性A,以0.6的概率设为是,0.4的概率设为否.
• 丢弃有缺失值的样本