Java开发之八大排序算法

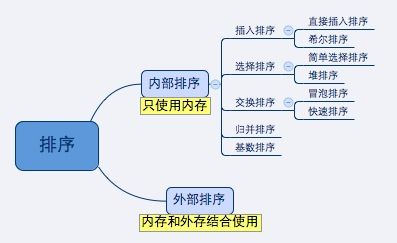
八大排序之间的关系:

1.直接插入排序

1)原理：将数组分为无序区和有序区两个区，然后不断将无序区的第一个元素按大小顺序插入到有序区中去，最终将所有无序区元素都移动到有序区完成排序。

2)要点：设立哨兵，作为临时存储和判断数组边界之用。

3)实例:

package sort;

public class InsertSort {
    public static void insertSort() {
        int a[] = {38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,15,35,25,53,51};
        int temp = 0;
        for(int i=1;i<a.length;i++) {
            int j = i - 1;
            temp = a[i];
            for(;j>=0&&temp<a[j];j--) {
                a[j+1]=a[j];//将大于temp的值整体后移一个单位 
            }
            a[j+1]=temp;
        }
        printArr(a);
    }
}

2.希尔排序(增量缩小排序)

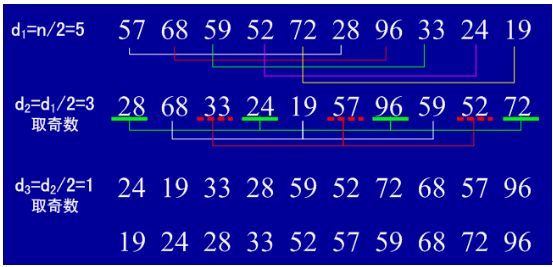
1)原理：又称增量缩小排序。算法先将要排序的一组数按某个增量d（n/2,n为要排序数的个数）分成若干组，每组中记录的下标相差d.对每组中全部元素进行直接插入排序，然后再用一个较小的增量（d/2）对它进行分组，在每组中再进行直接插入排序。当增量减到1时，进行直接插入排序后，排序完成。

2)要点：增量的选择以及排序最终以1为增量进行排序结束。

3)实例:

public static void shellSort(){
    int a[] = {34,1,54,6,3,78,12,45,56,100};
    double d1 = a.length;
    int temp = 0;
    while(true){
        d1 = Math.ceil(d1/2);//向上取整计算
        int d = (int)d1;
        for(int x=0;x<d;x++) {
            for(int i=x+d;i<a.length;i+=d){
                int j=i-d;
                temp = a[i];
                for(;j>=0&&temp<a[j];j-=d) {
                    a[j+d] = a[j];
                }
                a[j+d] = temp;
            }
        }
        if(d == 1){
            break;
        }
    }
    printArr(a);
}

3.简单选择排序

1)原理:在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

2)实例:

public static void selectSort(){
    int a[] = {190,1,54,6,3,78,34,12,45};
    int position = 0;
    for(int i=0;i<a.length;i++){
        int j=i+1;
        position = i;
        int temp = a[i];
        for(;j<a.length;j++){
            if(a[j] < temp) {
                temp = a[j];
                position = j;
            }
        }
        a[position] = a[i];
        a[i] = temp;
    }
    printArr(a);
}

4.堆排序

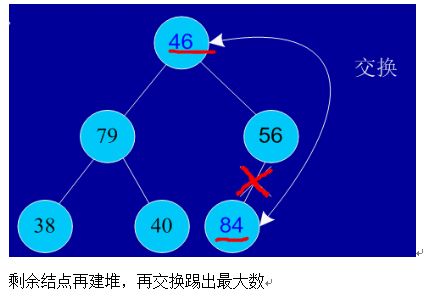
1)原理：利用大根堆或小根堆思想，首先建立堆，然后将堆首与堆尾交换，堆尾之后为有序区。

2)定义:具有n个元素的序列（h1,h2,…,hn),当且仅当满足（hi>=h2i,hi>=2i+1）或（hi<=h2i,hi<=2i+1） (i=1,2,…,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出，堆顶元素（即第一个元素）必为最大项（大顶堆）。完全二叉树可以很直观地表示堆的结构。堆顶为根，其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树，调整它们的存储序，使之成为一个堆，这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推，直到只有两个节点的堆，并对它们作交换，最后得到有n个节点的有序序列。从算法描述来看，堆排序需要两个过程，一是建立堆，二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数，二是反复调用渗透函数实现排序的函数。

3)要点：建堆、交换、调整堆

4)实例

初始序列：46,79,56,38,40,84

建堆：

交换，从堆中踢出最大数:

依次类推：最后堆中剩余的最后两个结点交换，踢出一个，排序完成。

public static void HeapSort(){
    int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,0,4,62,99,98,-12,54,56,17,18,23,34,15,35,25,53,51}; 
    int arrayLength = a.length;
    //循环建堆
    for(int i=0;i<arrayLength-1;i++) {
        //建堆
        buildMaxHeap(a,arrayLength-1-i);
        //交换堆顶和最后一个元素
        swap(a,0,arrayLength-1-i);
    }
    printArr(a);
}

private static void swap(int[] a, int i, int j) {
    int tmp = a[i];
    a[i] = a[j];
    a[j] = tmp;
}

//对a数组从0到lastIndex建大顶堆
private static void buildMaxHeap(int[] a, int lastIndex) {
    //从lastIndex处节点（最后一个节点）的父节点开始 
    for(int i=(lastIndex-1)/2;i>=0;i--){
        //k保存正在判断的节点
        int k = i;
        //如果当前k节点的子节点存在
        while(k*2+1 <= lastIndex){
            //k节点的左子节点的索引
            int biggerIndex = 2*k+1;
            //如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
            if(biggerIndex<lastIndex){
                //如果右子节点的值较大
                if(a[biggerIndex] < a[biggerIndex+1]) {
                    //biggerIndex总是记录较大子节点的索引
                    biggerIndex++;
                }
            }
            //如果k节点的值小于其较大的子节点的值
            if(a[k] < a[biggerIndex]) {
                //交换它们
                swap(a,k,biggerIndex);
                //将biggerIndex赋予k,开始while循环的下一次循环,重新保证k节点的值大于其左右子节点的
                k = biggerIndex;
            }else {
                break;
            }
        }
    }
}

5.冒泡排序

1)原理:在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

2)实例:

public static void bubbleSort(){
    int a[]={49,38,65,97,76,13,27,49,78,34,-12,64,5,4,62,99,98,54,56,0,17,18,23,34,15,35,25,53,51}; 
    int temp = 0;
    for(int i=0;i<a.length-1;i++) {
        for(int j=0;j<a.length-1-i;j++){
            if(a[j] > a[j+1]) {
                temp = a[j];
                a[j] = a[j+1];
                a[j+1] = temp;
            }
        }
    }
    printArr(a);
}

6.快速排序

1)基本思想：选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描，将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。

2)要点：递归、分治

3)实例：

public static void quickSort(){
    int a[]={49,38,65,97,76,13,27,49,78,34,-12,64,5,4,62,99,98,54,56,1,0,7,18,23,34,15,35,25,53,51};
    if(a.length > 0) {
        _quickSort(a,0,a.length-1);
    }
    printArr(a);
}

private static void _quickSort(int[] a, int low, int high) {
    if(low < high) {
        int middle = getMiddle(a,low,high);//将a数组进行一份为二
        _quickSort(a,low,middle - 1);//对低字表进行递归排序
        _quickSort(a,middle +1,high);//对高字表进行递归排序
    }
}

private static int getMiddle(int[] a, int low, int high) {
    int tmp = a[low];
    while(low < high) {
        while(low < high && a[high] >= tmp) {
            high--;
        }
        a[low] = a[high];//比中轴小的记录移到低端
        while(low < high && a[low] <= tmp) {
            low++;
        }
        a[high] = a[low];////比中轴大的记录移到高端
    }
    a[low] = tmp;//中轴记录到尾 
    return low;//返回中轴的位置
}

7. 归并排序

1)原理：归并（Merge）排序法是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

2)要点：归并、分治

3)实现：

public static void mergingSort(){
    int a[]={49,38,65,97,76,13,27,49,78,0,11,34,12,64,5,4,-62,99,98,54,56,17,18,23,34,15,35,25,53,51};
    sort(a,0,a.length-1);
    printArr(a);
}
private static void sort(int[] a, int left, int right) {
    if(left < right) {
        //找出中间索引
        int center = (left + right) / 2;
        //对左边数组进行递归
        sort(a,left,center);
        //对右边数组进行递归
        sort(a,center+1,right);
        //合并
        merge(a,left,center,right);
    }
}

private static void merge(int[] a, int left, int center, int right) {
    int[] tmpArr = new int[a.length];
    int mid = center + 1;
    //third记录中间数组的索引
    int third = left;
    int tmp = left;
    while(left <= center && mid <= right) {
        //从两个数组中取出最小的放入中间数组
        if(a[left] <= a[mid]) {
            tmpArr[third++] = a[left++];
        }else {
            tmpArr[third++] = a[mid++];
        }
    }
    //剩余部分依次放入中间数组
    while(mid <= right) {
        tmpArr[third++] = a[mid++];
    }
    while(left <= center) {
        tmpArr[third++] = a[left++];
    }
    //将中间数组中的内容复制回原数组
    while(tmp <= right){
        a[tmp] = tmpArr[tmp++];
    }
}

8.基数排序

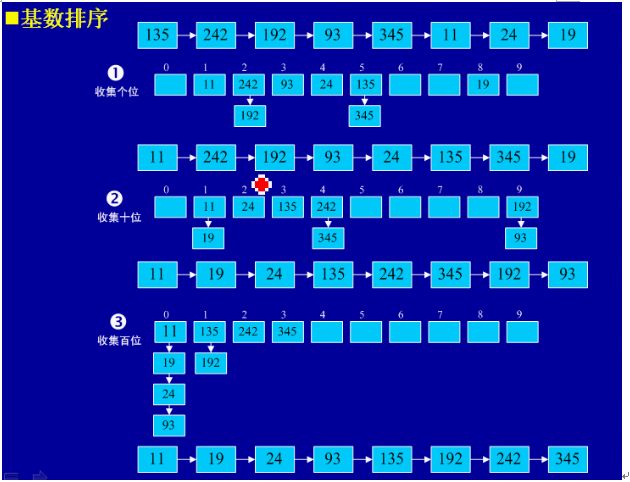
1)原理：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。

2)要点：对关键字的选取，元素分配收集。

3)实现：

public static void radixSort(){
    int a[]={49,38,65,97,76,13,2,7,49,78,3,4,12,64,0,11,5,4,62,99,98,54,101,56,17,18,23,34,15,35,25,53,51}; 
    sort(a);
    printArr(a);
}

private static void sort(int[] a) {
    //首先确定排序的趟数
    int max = a[0];
    for(int i=1;i<a.length;i++) {
        if(a[i] > max) {
            max = a[i];
        }
    }
    int time = 0;
    //判断位数
    while(max > 0) {
        max /= 10;
        time++;
    }
    //建立10个列队
    List<ArrayList> queue = new ArrayList<ArrayList>();
    for(int i=0;i<10;i++) {
        ArrayList<Integer> queue1 = new ArrayList<Integer>();
        queue.add(queue1);
    }
    //进行time次分配和收集
    for(int i=0;i<time;i++) {
        //分配数组元素
        for(int j = 0;j<a.length;j++) {
            //得到数字的第time+1位数
            int x = Math.abs(a[j] % (int)Math.pow(10, i+1)/(int)Math.pow(10, i)); //正整数
            ArrayList<Integer> queue2 = queue.get(x);
            queue2.add(a[j]);
            queue.set(x,queue2);
        }
        int count = 0;//元素计数器
        //收集队列元素
        for(int k = 0;k<10;k++) {
            while(queue.get(k).size() >0) {
                ArrayList<Integer> queue3 = queue.get(k);
                a[count] = queue3.get(0);
                queue3.remove(0);
                count++;
            }
        }
    }
}

代码戳Here