B-树
B-tree树即B树,B即Balanced,平衡的意思。因为B树的原英文名称为B-tree,而国内很多人喜欢把B-tree译作B-树,其实,这是个非常不好的直译,很容易让人产生误解。如人们可能会以为B-树是一种树,而B树又是另一种树。而事实上是,B-tree就是指的B树。B-树(百度百科)是由R.Bayer和E.M.McCreight与1972提出的一种多路平衡查找树,当查找的文件较大且存放在直接存取设备中时,能够有效地减少查找过程对文件的读取次数,提高查找效率。
定义:
B-树是一种多路平衡查找树,在文件系统中有所应用。主要用作文件的引索。
一棵m阶的B-树,或为空树,或者满足一下性质。
(1)每棵树只有一个根结点,根结点的关键字的范围[1,m-1];
(2)根结点至少有两颗子树。
(3)每个节点最多有m棵子树。
(4)除根节点和叶子节点外的非终端结点,所有的节点至少有[m/2](向上取整)个子树。
(5)非叶子节点的关键字范围[[m/2]-1,m-1];
(6)所有的叶子节点位于同一层。
(7)节点的关键字个数比子树个数少一。
(8)所有非终端结点包含下列信息
(n,A0,K1,A2,K2,....Kn,An)
其中Ki(i=1,2,3,...n)为关键字且Ki<Ki+1;Ai(i=0,1,2,...n)为指向子树的根结点的指针,且Ki小于Ai所指子树的所有关键字值(换而言之Ki大于Ai-1的所有子树关键字的值)。
下图是典型的3阶B-树
B-树结构定义
typedef struct BTNode{
int keynum;
struct BTNode *parent;//父节点
KeyType key[m+1];//关键字
struct BTNode *ptr[m+1];//孩子节点
}BTNode,*BTree;//辅助的result结构体
typedef struct{
BTNode *pt;//指向要插入的节点
int i;//插入的位置
int tag;//1:查找成功;2:查找失败
}Result;
基本操作:
主要讲解插入和删除操作,查找操作各大教材上面都有,就不在赘述:
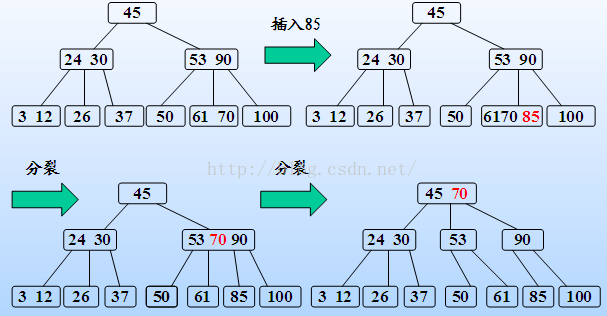
1)B-树的插入操作(关键是判断m的关键字个数是否达到上限m-1)
(a)利用查找算法找到插入的位置,若找得到,则说明该关键字,直接返回。否则返回将要插入的结点和位置。
(b)判断该节点是否存在空位置,即判断该节点关键总数n<=m-1;如果满足,则说明该节点还有空位置,则将关键字直接插入该节点中适当的位置。若不满足,则说明该节点已经没有空位置了,需要将该节点分裂成两个。
分裂方法:生成一新节点。将原点上的关键字和K(即要插入的关键字),然后从中间位置将关键字分成两个部分(不包含中间位置关键字),左部分所含关键字放在旧结点中,右部分所含的关键字放在新生成的结点当中,中间关键字连同新生成节点插入到父节点中。如果父节点关键字总数不满足n<=m-1,则重复上述操作,继续向上分裂.
注意:关键字的插入应该先在叶子节点上面操作。即找到合适的叶子节点进行插入操作,而不是在非终端结点上面直接插入。
B-树的删除操作
删除操作的重点是判断该节点的关键字总数是否满足n>=[m/2]-1(后面默认[m/2]表示m/2之后向上取整),根据性质4可得,B-树的删除也主要分为两步。
(a)首先利用B-树的查找算法判断该节点是否为叶子节点。若为叶子节点则根据不同的情况进行相应的操作。
(b)若该节点为非叶子节点,且该节点要删除的关键字为K[i],自在A[i]中找到最小的关键字Y替代K[i],然后在叶子节点中去掉Y;
在B-树的叶子节点中删除一个关键字的方法:
首先将要删除的关键字在叶子节点中删除,然后根据不同的情况作相应的处理。
a.若被删关键字所在节点总数n>=[m/2],则直接删除该节点。
b.若被删关键字所在节点总数n=[m/2]-1,删除之后则不满足B-树的定义,需要对B-树进行调整
调整过程为:如果其左右兄弟结点中有“多余”的关键字,即与该结点相邻的右(左)兄弟结点中的关键字数目大于ceil(m/2)-1。则可将右(左)兄弟结点中最小(大)关键字上移至双亲结点。而将双亲结点中小(大)于该上移关键字的关键字下移至被删关键字所在结点中。
c.如果左右兄弟结点中没有“多余”的关键字,即与该结点相邻的右(左)兄弟结点中的关键字数目均等于ceil(m/2)-1。这种情况比较复杂。需把要删除关键字的结点与其左(或右)兄弟结点以及双亲结点中分割二者的关键字合并成一个结点,即在删除关键字后,该结点中剩余的关键字加指针,加上双亲结点中的关键字Ki一起,合并到Ai(即双亲结点指向该删除关键字结点的左(右)兄弟结点的指针)所指的兄弟结点中去。如果因此使双亲结点中关键字个数小于ceil(m/2)-1,则对此双亲结点做同样处理。以致于可能直到对根结点做这样的处理而使整个树减少一层。
总之,设所删关键字为非终端结点中的Ki,则可以指针Ai所指子树中的最小关键字Y代替Ki,然后在相应结点中删除Y。对任意关键字的删除都可以转化为对最下层关键字的删除。
a、被删关键字Ki所在结点的关键字数目不小于ceil(m/2),则只需从结点中删除Ki和相应指针Ai,树的其它部分不变。
b、被删关键字Ki所在结点的关键字数目等于ceil(m/2)-1,则需调整。调整过程如上面所述。
c、被删关键字Ki所在结点和其相邻兄弟结点中的的关键字数目均等于ceil(m/2)-1,假设该结点有右兄弟,且其右兄弟结点地址由其双亲结点指针Ai所指。则在删除关键字之后,它所在结点的剩余关键字和指针,加上双亲结点中的关键字Ki一起,合并到Ai所指兄弟结点中(若无右兄弟,则合并到左兄弟结点中)。如果因此使双亲结点中的关字数目少于ceil(m/2)-1,则依次类推键.
#include<stdio.h>
#include<stdlib.h>
#define m 3
#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0
typedef int Status;
typedef int KeyType;
int Min =m/2+m%2;
typedef struct BTNode{
int keynum;
struct BTNode *parent;//父节点
KeyType key[m+1];//关键字
struct BTNode *ptr[m+1];//孩子节点
}BTNode,*BTree;
typedef struct{
BTNode *pt;//指向找到的结点
int i;//关键字序号
int tag;//1:查找成功;2:查找失败
}Result;
Status InitBTree(BTree &bt);
int Search(BTree bt,KeyType K);
Result& SearchBTree(BTree T,KeyType K);
Status Insert(BTree &p,int i,KeyType K,BTree ap);
Status split(BTree &p,int s,BTree &ap);
Status NewRoot(BTree &T,BTree &q,KeyType K,BTree &ap);
Status InsertBTree(BTree &T,KeyType K,BTree q,int i);
Status CreateBTree(BTree &bt,KeyType *a,int N);
void Successor(BTree &p,int i,BTree &q);//
void Remove(BTree &p,int i);
void Restore(BTree &p,int i);
void MoveRight(BTree &p,int i);
void MoveLeft(BTree &p,int i);
void Combine(BTree &p,int i);
int RecDelete(BTree &p,KeyType K);
void DeleteBTree(BTree &p,KeyType K);
void PrintBTree(BTree);
int main()
{
int N,a[20];
BTree bt=NULL;
KeyType K;
Result r;
printf("元素个数:");
scanf("%d",&N);
printf("输入元素序列:");
for(int i=0;i<N;i++)
scanf("%d",&a[i]);
CreateBTree(bt,a,N);
PrintBTree(bt);
printf("输入删除关键字:");
scanf("%d",&K);
DeleteBTree(bt,K);
PrintBTree(bt);
return 0;
}
Status InitBTree(BTree &bt)
{
bt->keynum=0;
for(int i=0;i<=m;i++)
{
bt->key[i]=0;
bt->ptr[i]=NULL;
}
bt->parent=NULL;
return OK;
}
int Search(BTree bt,KeyType K)
{
if(K<bt->key[1])
return 0;
if(K>=bt->key[bt->keynum])
return bt->keynum;
for(int i=1;i<=bt->keynum-1;i++)
if(bt->key[i]<=K&&bt->key[i+1]>K)
return i;
if(bt->keynum==0)
return 0;
}
Result& SearchBTree(BTree T,KeyType K)
{
BTree p=T,q=NULL;
Result result;
int i=0,found=FALSE;
while(p&&!found)
{
i=Search(p,K);
if(i>0&&p->key[i]==K)
found=TRUE;
else
{
q=p;
p=p->ptr[i];
}
}
result.i=i;
if(found==TRUE)
{
result.pt=p;
result.tag=1;
}else
{
result.pt=q;
result.tag=0;
}
return result;
}
Status Insert(BTree &p,int i,KeyType K,BTree ap)
{
if(i==p->keynum)
{
p->key[i+1]=K;
p->ptr[i+1]=ap;
if(ap)
ap->parent=p;
p->keynum++;
}
else
{
p->keynum++;
for(int t=p->keynum;t>=i+2;t--)
{
p->key[t]=p->key[t-1];
p->ptr[t]=p->ptr[t-1];
}
p->key[i+1]=K;
p->ptr[i+1]=ap;
if(ap)
ap->parent=p;
}
return OK;
}
Status split(BTree &p,int s,BTree &ap)
{
int t=0;
ap=(BTree)malloc(sizeof(BTNode));
if(!ap)
{
printf("malloc error");
return ERROR;
}
InitBTree(ap);
for(int i = s + 1; i <= p->keynum; i++)
{
ap->key[i - s] = p->key[i];
ap->ptr[i - s] = p->ptr[i];
if(ap->ptr[i-s])
ap->ptr[i-s]->parent=ap;
}
ap->ptr[0]=p->ptr[s];
if(ap->ptr[0])
ap->ptr[0]->parent=ap;
ap->keynum=p->keynum-s;
//初始化前面的一段内容
for(int j=s;j<=p->keynum;j++)
{
p->key[j]=0;
p->ptr[j]=NULL;
}
p->keynum=s-1;
return OK;
}
Status NewRoot(BTree &T,BTree &q,KeyType K, BTree &ap)
{
int s,i;
if(!T)//当根节点为空的之后
{
T=(BTree)malloc(sizeof(BTNode));
if(!T)return ERROR;
InitBTree(T);
T->key[1]=K;
T->keynum++;
}
else//返回到最上面的顶点
{
s=T->keynum/2+T->keynum%2;
q=(BTree)malloc(sizeof(BTNode));
if(!q)return ERROR;
InitBTree(q);
q->key[1]=K;
q->ptr[0]=T;
q->ptr[1]=ap;
q->keynum++;
T->parent=q;
if(ap)
ap->parent=q;
T=q;
}
return OK;
}
Status InsertBTree(BTree &T,KeyType K,BTree q,int i)
{
KeyType x=K;
BTree ap=NULL;
int finished=FALSE;
int s;
while(q&&!finished)
{
Insert(q,i,x,ap);
if(q->keynum<m)
finished=TRUE;
else
{
s=m/2+m%2;
x=q->key[s];
split(q,s,ap);
q=q->parent;
if(q)
i=Search(q,x);
}
}
if(!finished)//分裂到最高结点,或者T为空树
NewRoot(T,q,x,ap);
return OK;
}
//创建一个B-Tree
Status CreateBTree(BTree &bt,KeyType *a,int N)
{
Result result;
for(int i=0;i<N;i++)
{
result=SearchBTree(bt,a[i]);
if(!result.tag)//B-Tree中没有该节点,插入
InsertBTree(bt,a[i],result.pt,result.i);
}
return OK;
}
void PrintBTree(BTree bt)
{
if(bt)
{
for(int i=1;i<=bt->keynum;i++)
printf("%d ",bt->key[i]);
printf("\n");
for(int t=0;t<=bt->keynum;t++)
PrintBTree(bt->ptr[t]);
}
}
void DeleteBTree(BTree &bt,KeyType K)
{
BTree p;
if(RecDelete(bt,K)==0)
printf("关键字%d不在B-树中\n",K);
else
{
printf("删除成功!\n");
if(bt->keynum==0)
{
p=bt;
bt=bt->ptr[0];
free(p);
}
}
}
int RecDelete(BTree &p,KeyType K)
{
int i,j,found;
BTree q,t=NULL,s;
Result r;
KeyType P;
if(p==NULL)
return 0;
else
{
r=SearchBTree(p,K);
i=r.i;
q=r.pt;
if(r.tag==1)//找到了该节点
{
if(q->ptr[i-1])//该节点为非叶子节点
{
Successor(q,i,t);//将该节点删除后,从q.ptr[i]中将最小的位置给他
P=t->key[1];
Remove(t,1);
if(t->keynum<Min-1)
{
j=Search(t->parent,P);
Restore(t->parent,j);
}
}
else
{
t=q->parent;
j=Search(t,K);
Remove(q,i);//删除叶子节点中的关键字
if(q->keynum<Min-1)
Restore(t,j);
}
}
}
return r.tag;
}
void Successor(BTree &p,int i,BTree &q)
{
BTree t;
for(q=p->ptr[i];q!=NULL;t=q,q=q->ptr[0])
p->key[i]=q->key[1];
q=t;
}
void Remove(BTree &p,int i)
{
for(int j=i;j<=p->keynum;j++)
{
p->key[i]=p->key[i+1];
p->ptr[i]=p->ptr[i+1];
}
p->key[p->keynum]=0;
p->ptr[p->keynum]=NULL;
--p->keynum;
}
void Restore(BTree &p,int i)
{
//shan删除关键字后,调整整个B-
if(i==0)
{
if(p->ptr[1]->keynum>Min-1)
MoveLeft(p,i);
else
Combine(p,1);
}
else if(i==p->keynum)
{
if(p->ptr[p->keynum-1]->keynum>Min-1)
MoveRight(p,i);
else
Combine(p,p->keynum);
}
else//其他情况即为既有左子树,又有右子树
{
if(p->ptr[i+1]->keynum>Min-1)
MoveLeft(p,i);
else if(p->ptr[i-1]->keynum>Min-1)
MoveRight(p,i);
else
Combine(p,i);
}
}
void MoveRight(BTree &p,int i)
{
BTree q;
q=p->ptr[i];
q->keynum++;
for(int t=q->keynum;t>=2;t--)
{
q->key[t]=q->key[t-1];
q->ptr[t]=q=q->ptr[t-1];
}
q->ptr[1]=q->ptr[0];
q->key[1]=p->key[i];
q=p->ptr[i-1];
p->key[i]=q->key[q->keynum];
q->key[q->keynum]=0;
q->ptr[q->keynum]=NULL;
q->keynum--;
}
void MoveLeft(BTree &p,int i)
{
BTree q;
q=p->ptr[i];
q->keynum++;
q->key[q->keynum]=p->key[i+1];
q=p->ptr[i+1];
p->key[i+1]=q->key[1];
for(int t=1;t<=q->keynum-1;t++)
{
q->key[t]=q->key[t+1];
q->ptr[t]=q->ptr[t+1];
}
q->key[q->keynum]=0;
q->keynum--;
}
void Combine(BTree &p,int i)
{
int c;
BTree q;
BTree l;
q=p->ptr[i];
l=p->ptr[i-1];
l->keynum++;
l->key[l->keynum]=p->key[i];
//合并两个叶子节点
for(c=l->keynum+1;c<=l->keynum+q->keynum;c++)
l->key[c]=q->key[c-l->keynum];
l->keynum+=q->keynum;
//删除父节点中分割的关键字
for(c=i;c<=p->keynum-1;c++)
{
p->key[c]=p->key[c+1];
p->ptr[c]=p->ptr[c+1];
}
p->key[p->keynum]=0;
p->ptr[p->keynum]=NULL;
p->keynum--;
free(q);
}