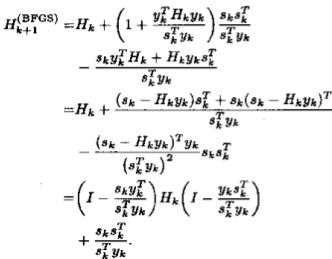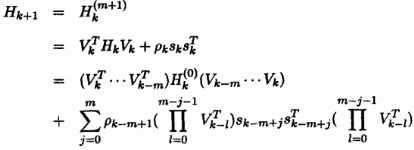大规模优化算法 - LBFGS算法
http://blog.sina.com.cn/s/blog_eb3aea990101gflj.html
L-BFGS算法比较适合在大规模的数值计算中，具备牛顿法收敛速度快的特点，但不需要牛顿法那样存储Hesse矩阵，因此节省了大量的空间以及计算资源。本文主要通过对于无约束最优化问题的一些常用算法总结，一步步的理解L-BFGS算法，本文按照最速下降法- 牛顿法 - 共轭梯度法 - 拟牛顿法 - DFP矫正 - BFGS 矫正 -LBFGS算法这样一个顺序进行概述。（读了一些文章之后，深感数学功底不够，在计算机视觉领域和机器学习领域，数学还是王道）
1. 最优化方法的迭代思想： 最优化方法采用的都是迭代的方法，基本思想是给定一个初始的点x_0，按照某一个迭代的规则产生一个点列{x_k}，在点列有限的情况下最后一个x_k就为最优解，当点列无穷的时候，则极限点为最优解。基本的迭代方程形式如下：
其中x_k就是迭代点列中的点，d_k为第k次搜索的方向，a_k为步长。
在所有的优化方法中三个关键的因素是：初始值x_0,方向d_k以及步长a_k，因此在一般的对于优化算法的学习，只需要搞懂这三个东西是怎么生成的，也就可以了。进一步理解则需要对于其理论进行深入的分析了。
2. 最速下降法（Gradientdescent）：GD算法是无约束最优化算法中最简单的一种算法，它的各种变种也被应用到大规模的机器学习任务中来，比如SGD，batchGD，mini-batch等。
GD算法的一个基本假设就是函数f(x)在x_k处是连续可谓的，并且其导数g_k在x_k处不为0.将一个函数在x_k这一点做一阶的泰勒展开，得到：
优化的目的是让函数值随着点列{x_k}的渐进，逐渐下降，在上式中就是让f(x)小于f(x_k)，如何达到这一个目的呢。
由于泰勒展开余项的值相对很小，因此我们可以忽略它。看第二项 ，如果它为负值，就可以达到我们的目的。记，那么
的方向d_k就是下降的方向，这个方向有无穷多个，那那个最大呢，由Cauchy-Schwartz不等式，有
这样我么可以很容易的推导出当且仅当时候，第二项最小，由此得到最速下降法的迭代公式
这里需要注意的是，最速下降方向仅仅是算法的局部性质，也就是说在局部它是一个下降最快的方向，并不是在全局上。在极值点附近，步长越小，前进越慢。
3. 牛顿法（Newtonmethod）
最速下降法采用的泰勒的一阶展开，而牛顿法采用的是泰勒二阶展开。
对于正定的二次函数，牛顿法一步就可以达到最优解，也就是不用迭代，就是解析解。而对于非二次函数，牛顿法并不能保证经过有限次迭代就可以求得最优解。有一点是在极小点附近目标函数接近于二次函数，因此其收敛速度一般是快的（2阶收敛速度）。另外需要注意的是牛顿法需要计算二阶导也就是hesse矩阵，因此需要较大的存储空间和计算量，在大规模的数值计算中直接使用牛顿法是不合适的。
4. 共轭梯度法(ConjugateGradient)：共轭梯度法是介于GD和Newton法之间的一个方法，它仅仅需要利用一阶导数的信息，克服了GD方法收敛慢的特点，由避免了计算和存储Hesse矩阵信息。其基本思想是把共轭性与最速下降方法相结合，利用已知点处的梯度构造一组共轭方向，并沿这组方向进行搜素，求出目标函数的极小点。
共轭：对于任意两个n维向量d1，d2来说，如果对于对于一个n*n对称正定矩阵，满足则称d1，d2是G共轭的，同时它们也就是线性无关的。假设我们所要求的函数具有以下形式（这个形式和牛顿法的那个二阶展开是否很像，G是二阶导数矩阵，G正定？，这一点是BFGS算法的核心点，下面会提到）。
导数矩阵为
共轭梯度法关键点是如何找共轭的方向，同时保证函数下降。一般说来，基本的假设是当前的搜索方向是当前梯度和前面所有梯度的一个线性组合，这个假设在一定程度上是合理的：每一个下降方向都是和前面的相关的，并不是完全无关的。初始化一个d_0方向，根据这个假设可以得到:
其中beta就是关于上一方向的系数，而beta如何计算？我们如果有了一个对称的正定矩阵G，beta可以由下面的公式来计算（由上式子，和共轭条件推导得来）
这样最后可以得到最终的共轭梯度法的计算公式：
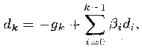
总结以下4个属性
a.同一点处的搜索方向与梯度的点积等于该点处的负梯度与梯度的点积，
b.某一点处的梯度与前面所有搜索方向的点积为0，
c.某一点处的梯度与前面所有梯度的点积为0，
d .某一点处的搜索方向与前面所有搜索方向共轭。
在一个需要特别指出的一点：共轭梯度法只使用到了函数的一阶导数的，而没有涉及到二阶导数，在beta的计算中给消掉了，所以不用计算和存储Hesse矩阵了。但是共轭方法经过n步迭代之后，产生的新方向可能不再有共轭性，需要进一步的修正，比如从新取负梯度方向为下降方向等。
5.拟牛顿法（Quasi-Newton）
在牛顿法中，函数的Hesse矩阵实际上提供的是函数的曲率，但是计算Hesse矩阵在很多情况下并不是很方便的事情，在高纬的情况下，存在计算量大，需要较大的存储空间的问题，人们想到能不能不显示的计算Hesse矩阵，而是利用一个和Hesse矩阵的近似来替代它呢，这就是拟牛顿法的初衷也是它名字的由来。
拟牛顿法的核心思想是：构造与Hesse矩阵相似的正定矩阵，而这个构造方法计算量比牛顿法小。其实可以发现上面讲的共轭梯度法也避免了Hesse矩阵的直接计算，一定程度上可以认为拟牛顿法是共轭梯度法的兄弟。
首先将目标函数展成二阶的泰勒级数，（和3中的牛顿法的表示略有不同，只是为了后边书写的方便，其实是一样的）
目标是推导一个G的近似，因此上面两边对x求导，可以得到
令 可以得到
再变化一下，得到
此处的H表示的是G的逆的近似，这个公式就是逆牛顿条件或者逆牛顿方程。同时我们也可以这样来写这个方程
此处的B表示的就是G的近似，也是BFGS公式推导的一个基础。以上两个公式互为对偶。
总结一下，如果我们使用H来替代原来牛顿方法中的G的逆，就变成了拟牛顿法。如何拟合H变成了重点。
在拟牛顿法中有两个重要的方法，一个是DFP（Davidon、Fletcher、Powell三人的首字母）方法，由Davidon（1959）提出，Felether和Powell（1963）发展，一个就是BFGS方法。下面分别来讨论一下。
6. 拟牛顿法 - DFP
DFP算法的矫正公式为
这个公式是由对于矩阵的秩二矫正（ranktwo update）推导而来的，设u，v为任意的n维向量，构造：
带入拟牛顿条件可以得到：
为了使得上述公式成立，做如下的构造：
这样公式就成立了，由此导出了DFP算法的矫正公式。
7. 拟牛顿法 - BFGS
到这里我们终于距离L-BFGS算法越来越接近了。关于B的BFGS矫正公式如下
利用两次Sharman-Morrison的逆的rank one update就可以得到关于H的BFGS矫正公式
Sharman-Morrison 定理(如下式)是描述的如何求秩一校正后的矩阵的逆矩阵：
其实B_k就是H_k的逆矩阵，利用这个定理可以对于B的BFGS矫正公式的右端求逆矩阵，从而可以得到关于H的BFGS矫正。
8. L-BFGS算法
在上述的BFGS算法的计算过程中，H_k逐渐的变得稠密，因此计算量逐渐正大。为了避免这个问题，LBFGS算法做了以下的改进：
a) 在每一步估算hesse矩阵的近似的时候，给出一个当前的初始估计H0
b) 利用过去的m-1次的曲率信息修正H0直到得到最终的Hesse矩阵。
在关于H的BFGS矫正中，令
得到
然后给定m，则迭代m+1次后得到此时的H
写出H的最终表达式为
初始值由以下公式给出。
L-BFGS算法的优点是，它不需要记忆H或者B这两个近似矩阵，而只需要存储{si，yi}的一个序列，这样就大大节省了存储空间。
9. 在@夏粉_百度 的几次讲座中都提到了LBFGS算法，并提到百度首创的Shooting算法，既然是和LBFGS算法比较的，相必也应该是从这个算法出发的，提出的一些改进。可以看到Shooting算法在初始的时候下降的非常快，收敛速度比LBFGS要快一些，具体怎么做的就不知道了。
顺便提一下，LBFGS构造的H并不一定是最优的下降方向，但保证正定，也就是函数一定会下降，估计Shooting算法会在这个最优方向上做文章。
10. 总结：
从LBFGS算法的流程来看，其整个的核心的就是如何快速计算一个Hesse的近似：重点一是近似，所以有了LBFGS算法中使用前m个近似下降方向进行迭代的计算过程；重点二是快速，这个体现在不用保存Hesse矩阵上，只需要使用一个保存后的一阶导数序列就可以完成，因此不需要大量的存储，从而节省了计算资源；重点三，是在推导中使用秩二校正构造了一个正定矩阵，即便这个矩阵不是最优的下降方向，但至少可以保证函数下降。
参考文献：
1. 《最优化理论与方法》 袁亚湘 孙文瑜
2. http://blog.csdn.net/nocml/article/details/8287466
3. UpdatingQuasi-Newton Matrices with Limited Storage , JorgeNocedal
4. NonlinearProgramming, second edition, Dimitri P. Bertsekas
5. 《广告数据上的大规模机器学习》 夏粉