(日志,《算法导论》.6.4)优先队列,堆,代码
堆形式:MAX-HEADIFY
/***********************************************************************************
程序名称 :priorityqueue_test
功能描述 : MAXpq,堆 , 优先队列,
修改历史 :
1.日 期 : 2015/10/6
作 者 : gqkly
内容 :
************************************************************************************/
#include <iostream>
#include <string>
#include <time.h>
#include <stdio.h>
using namespace std;
typedef int ElemType;
#define InitHeap(heap,len) { memset(&heap,0,sizeof(heap));heap.length=len;}
#define InitHeapA(heap) {heap.A=(ElemType*)malloc(heap.length*sizeof(ElemType));for(int i=0;i<heap.length;i++)heap.A[i]=rand()%50;}
#define Right_Of_I(i) (2*i+1)
#define Left_Of_I(i) (2*i)
#define Right_Parent(i) ((i-1)>>2)
#define Left_Parent(i) (i>>2)
#define swap1(a,b) {a=a+b;b=a-b;a=a-b;}
#define swap2(a,b) {a=a+b-(b=a);}
#define swap3(a,b) {b=a+(a=b)*0;}
#define swap4(a,b) {a=a^b;b=a^b;a=a^b;}
#define N 10
typedef struct HEAP_TYPE
{
ElemType *A;
int length;
}HEAP,*HEAP_PTR;
//最大优先队列相关函数
ElemType Heap_Get_Maxnum(HEAP heap);//返回最大元素,即数学位置1的元素
ElemType Heap_Extract_Max(HEAP *heap);//返回最大元素,即数学位置1的元素,并删除它,之后仍然要维持性质
void Heap_Increase_Key(HEAP *heap,int i,ElemType key);//增大数学位置i的元素的key
void Max_Heap_Insert(HEAP *heap,ElemType key);//插入一个新的元素
//之下是维护堆性质的函数
void Max_Heapify(HEAP* heap,int i);//中间层和第三层
void Build_Max_Heap(HEAP* heap);//中间层
void Heap_Sort(HEAP* heap);//第一层函数
void Print_Heap(HEAP heap,char *string);
int main()
{
HEAP heap;
InitHeap(heap,N);
InitHeapA(heap);//随机初始化堆内容
Print_Heap(heap,"Init heap:");
Build_Max_Heap(&heap);
Print_Heap(heap,"Builded heap:");
int max_num=Heap_Get_Maxnum(heap);
cout<<"\nGet_Maxnum:"<<max_num<<endl;
Print_Heap(heap,"Heap_Get_Maxnum:");
max_num=Heap_Extract_Max(&heap);
cout<<"\nGet_Maxnum:"<<max_num<<endl;
Print_Heap(heap,"Heap_Extract_Max:");
Heap_Increase_Key(&heap,heap.length-3,34);
Print_Heap(heap,"Heap_Increase_Key:(length-3),34");
Max_Heap_Insert(&heap,35);
Print_Heap(heap,"Max_Heap_Insert:(35)");
getchar();
return 0;
}
ElemType Heap_Get_Maxnum(HEAP heap)
{
if (heap.length<0)
{
cout<<"\nerror: heap underflow"<<endl;
return -65532;
}
return heap.A[0];//数学位置1
}
ElemType Heap_Extract_Max(HEAP *heap)
{
if ((*heap).length<0)
{
cout<<"\nerror: heap underflow"<<endl;
return -65532;
}
int max_num=(*heap).A[0];
(*heap).A[0]=(*heap).A[(*heap).length-1];//把最后一个元素移到首位以维护堆性质
(*heap).length--;
Max_Heapify(heap,1);//传入的是数学位置,内部会修正为数组下标
return max_num;
}
void Heap_Increase_Key(HEAP *heap,int i,ElemType key)
{
int parent;
int pos=i-1;
if (key<=(*heap).A[pos])
{
cout<<"\nerror:new key is smaller";
return ;
}
(*heap).A[pos]=key;
if (i/2==0)
{
parent=Left_Parent(i)-1;
}
else
parent=Right_Parent(i)-1;
if (parent<0)
{
cout<<"\nerror: it has been the max num "<<endl;
return ;
}
while(pos>0&& ( ((*heap).A[parent]) < ( (*heap).A[pos]) ) )
{
swap1( (*heap).A[pos],(*heap).A[parent]);
pos=parent;
}
}
void Max_Heap_Insert(HEAP *heap,ElemType key)
{
(*heap).length++;
ElemType* tmp =(*heap).A+(*heap).length;
if ((*heap).length>N)
{
tmp=(ElemType*)malloc(sizeof(ElemType));
}
(*heap).A[(*heap).length-1]=-65532;
Heap_Increase_Key(heap,(*heap).length,key);
}
//一下是维护堆性质的函数
void Max_Heapify(HEAP* heap,int i)//这个参数i为数学位置,函数内部转化为数组坐标
{
int largest;
int l=Left_Of_I(i);
int r=Right_Of_I(i);
if ( (l<=(*heap).length) && ((*heap).A[l-1])>((*heap).A[i-1]) )
{
largest=l;
}
else
largest=i;
if ( (r<=(*heap).length) && ((*heap).A[r-1])>((*heap).A[largest-1]) )
{
largest=r;
}
if (largest!=i)
{
swap1( (*heap).A[i-1],(*heap).A[largest-1] );
Max_Heapify(heap,largest);
}
}
void Build_Max_Heap(HEAP* heap)
{
int len=(*heap).length;
for (int i=(len/2);i>0;i--)
{
Max_Heapify(heap,i);
}
}
void Heap_Sort(HEAP* heap)
{
int tmp_size=(*heap).length;
Build_Max_Heap(heap);
for (int i=(*heap).length-1;i>0;i--)//长度的大小和坐标不一样
{
swap1((*heap).A[0],(*heap).A[i]);
(*heap).length--;//此处通过减小堆大小来为排序服务,所以需要在之后还原
Max_Heapify(heap,1);//1是数学位置--第一个元素
}
(*heap).length=tmp_size;//还原堆大小
}
void Print_Heap(HEAP heap,char *string)
{
int tmp=0;
int t=2;
cout<<"***********************************************"<<endl;
cout<<string<<endl;
for (int i=0;i<heap.length;i++)
{
tmp=i+1;
if ((i+1)==t)
{
t*=2;
tmp=i+1;
cout<<endl;
}
cout<<heap.A[i]<<' ';
}
cout<<endl;
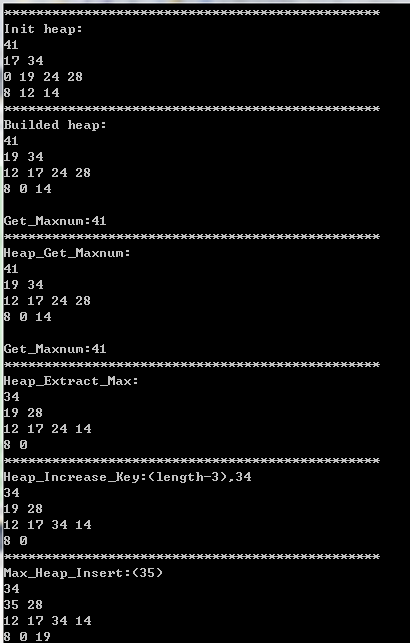
} 运行结果: