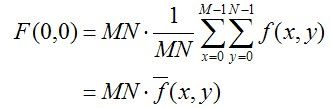理想高通滤波器
高通滤波器
首先,对一副图像进行如下二维傅里叶变换。
我们将u=0和v=0带上式,我们可以得到如下式子。
根据上式,可以到F(0,0)的值是非常大的。这里,我们将
F(0,0)称为直流分量,直流分量比其他的成分要大好几个数量级。所以,这也就是傅里叶谱为什么需要使用对数变换才能看清楚的原因。
这里,对于高通滤波器而言,由于直流分量被衰减,所以,所得到的图像的动态范围是非常狭窄的,也就造成了图像偏灰。进一步而言,保持直流(DC)分量,对别的部分进行增幅,可以增强图像的细节。这样的滤波器称为锐化滤波器。这一小节主要介绍高通滤波器与锐化滤波器。
理想高通滤波器的转移函数:
0, D(u,v) ≤ D0
H(u,v)=
1, D(u,v) > D0
下面是产生的3D滤波器的图
这是图像的对比效果
最后给一个代码,希望大家可以来参考
clear all
%读取图像
I=imread('testpat1.png');
J=double(I);
%分别设置3种不同的滤波半径
D1=15;
D2=30;
D3=50;
%傅里叶变换并中心化
Fuv=fftshift(fft2(J));
[M,N]=size(Fuv);
%确定傅里叶变换的原点
xo=floor(M/2);
yo=floor(N/2);
%分别求IHPF
for i=1:M
for j=1:N
D=sqrt((i-xo)^2+(j-yo)^2);
if(D>=D1)
h1(i,j)=1;
else
h1(i,j)=0;
end
if(D>=D2)
h2(i,j)=1;
else
h2(i,j)=0;
end
if(D>=D3)
h3(i,j)=1;
else
h3(i,j)=0;
end
end
end
%滤波 矩阵点乘
Guv1=h1.*Fuv;
Guv2=h2.*Fuv;
Guv3=h3.*Fuv;
%傅里叶逆变换
g1=ifftshift(Guv1);
g1=uint8(real(ifft2(g1)));
g2=ifftshift(Guv2);
g2=uint8(real(ifft2(g2)));
g3=ifftshift(Guv3);
g3=uint8(real(ifft2(g3)));
%分别显示各个图像
subplot(2,2,1);imshow(I);title('原图像')
subplot(2,2,2);imshow(g1);title('IHPF D0=15');
subplot(2,2,3);imshow(g2);title('IHPF D0=30');
subplot(2,2,4);imshow(g3);title('IHPF D0=50');