POJ 1324Holedox Moving (状态BFS)
Holedox Moving
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 15264 | Accepted: 3686 |
Description
During winter, the most hungry and severe time, Holedox sleeps in its lair. When spring comes, Holedox wakes up, moves to the exit of its lair, comes out, and begins its new life.
Holedox is a special snake, but its body is not very long. Its lair is like a maze and can be imagined as a rectangle with n*m squares. Each square is either a stone or a vacant place, and only vacant places allow Holedox to move in. Using ordered pair of row and column number of the lair, the square of exit located at (1,1).
Holedox's body, whose length is L, can be represented block by block. And let B1(r1,c1) B2(r2,c2) .. BL(rL,cL) denote its L length body, where Bi is adjacent to Bi+1 in the lair for 1 <= i <=L-1, and B1 is its head, BL is its tail.
To move in the lair, Holedox chooses an adjacent vacant square of its head, which is neither a stone nor occupied by its body. Then it moves the head into the vacant square, and at the same time, each other block of its body is moved into the square occupied by the corresponding previous block.
For example, in the Figure 2, at the beginning the body of Holedox can be represented as B1(4,1) B2(4,2) B3(3,2)B4(3,1). During the next step, observing that B1'(5,1) is the only square that the head can be moved into, Holedox moves its head into B1'(5,1), then moves B2 into B1, B3 into B2, and B4 into B3. Thus after one step, the body of Holedox locates in B1(5,1)B2(4,1)B3(4,2) B4(3,2) (see the Figure 3).
Given the map of the lair and the original location of each block of Holedox's body, your task is to write a program to tell the minimal number of steps that Holedox has to take to move its head to reach the square of exit (1,1).
Holedox is a special snake, but its body is not very long. Its lair is like a maze and can be imagined as a rectangle with n*m squares. Each square is either a stone or a vacant place, and only vacant places allow Holedox to move in. Using ordered pair of row and column number of the lair, the square of exit located at (1,1).
Holedox's body, whose length is L, can be represented block by block. And let B1(r1,c1) B2(r2,c2) .. BL(rL,cL) denote its L length body, where Bi is adjacent to Bi+1 in the lair for 1 <= i <=L-1, and B1 is its head, BL is its tail.
To move in the lair, Holedox chooses an adjacent vacant square of its head, which is neither a stone nor occupied by its body. Then it moves the head into the vacant square, and at the same time, each other block of its body is moved into the square occupied by the corresponding previous block.
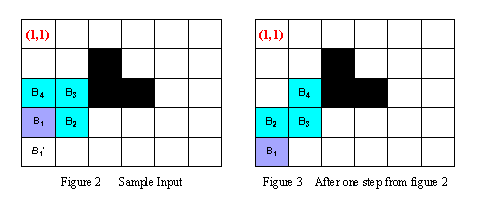
For example, in the Figure 2, at the beginning the body of Holedox can be represented as B1(4,1) B2(4,2) B3(3,2)B4(3,1). During the next step, observing that B1'(5,1) is the only square that the head can be moved into, Holedox moves its head into B1'(5,1), then moves B2 into B1, B3 into B2, and B4 into B3. Thus after one step, the body of Holedox locates in B1(5,1)B2(4,1)B3(4,2) B4(3,2) (see the Figure 3).
Given the map of the lair and the original location of each block of Holedox's body, your task is to write a program to tell the minimal number of steps that Holedox has to take to move its head to reach the square of exit (1,1).
Input
The input consists of several test cases. The first line of each case contains three integers n, m (1<=n, m<=20) and L (2<=L<=8), representing the number of rows in the lair, the number of columns in the lair and the body length of Holedox, respectively. The next L lines contain a pair of row and column number each, indicating the original position of each block of Holedox's body, from B1(r1,c1) to BL(rL,cL) orderly, where 1<=ri<=n, and 1<=ci<=m,1<=i<=L. The next line contains an integer K, representing the number of squares of stones in the lair. The following K lines contain a pair of row and column number each, indicating the location of each square of stone. Then a blank line follows to separate the cases.
The input is terminated by a line with three zeros.
Note: Bi is always adjacent to Bi+1 (1<=i<=L-1) and exit square (1,1) will never be a stone.
The input is terminated by a line with three zeros.
Note: Bi is always adjacent to Bi+1 (1<=i<=L-1) and exit square (1,1) will never be a stone.
Output
For each test case output one line containing the test case number followed by the minimal number of steps Holedox has to take. "-1" means no solution for that case.
Sample Input
5 6 4 4 1 4 2 3 2 3 1 3 2 3 3 3 3 4 4 4 4 2 3 1 3 1 4 2 4 4 2 1 2 2 3 4 4 2 0 0 0
Sample Output
Case 1: 9 Case 2: -1
Hint
In the above sample case, the head of Holedox can follows (4,1)->(5,1)->(5,2)->(5,3)->(4,3)->(4,2)->(4,1)->(3,1)->(2,1)->(1,1) to reach the square of exit with minimal number of step, which is nine.
这是一道很有意义的题（对我而言），它帮我更好的理解了我一直恐惧的状态压缩
题意：给出蛇头和蛇身（蛇身分为若干节，用坐标连起来，当然蛇头也是一个坐标）
给出终点坐标，障碍物坐标，问蛇能不能到达终点（蛇头到达）
分析：
蛇身的移动是根据蛇头来的，所以以蛇头进行BFS搜索，我最初很单纯的用二维vis将蛇头走过的点标记，
然后使劲wa，后来问了某大神才顿悟，蛇头在同一点但是蛇身可能不同啊，这样引起的结果就不同，也就是说，
vis数组还需要将整个蛇身保存下来！！！
怎么保存？把蛇占据的坐标全部记录下来？那太不现实了！
当我们模拟蛇移动的时候会发现，假设将蛇身分为0,1,2...i....节，那么在蛇移动的过程中，第i节将走的原本
第i-1节的位置（设蛇头为0），反正意思就是是跟着蛇头走的这点可以利用
试想，如果我们有蛇头的坐标，和每一节蛇身的方向，能不能确定蛇身，显然是可以的！
为什么这样记录呢，蛇身的坐标可选太多了，而蛇身移动的方向只有4个
蛇身也不长，所以完全可以用四进制记录蛇身，四进制的话每一位可以有0,1,2,3四个数字，就可以很好的
描述四个方向
之所以说这题让我不再恐惧状压是因为，我发现其实所谓的二进制，完全可以看成一个数组，
比如01101010就可以看成长度为8的数组a，a[0] = 0,a[1] = 1,a[2] = 1...
这个特殊的数组保存了每个物品的状态，并用一个十进制数保存下来，比正常的数组更省空间，
而要用好这个数组关键在于如何从数组中取元素，如何将更新后的值重新构建成新的数组
这就是要用各种逻辑运算符了。。。
如果按二进制数是一个数组来想，其实二进制转十进制算是一种天然的哈希，这样，状态压缩就更好理解了
废话不说了，show you the code :
//Must so
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#define mem(a,x) memset(a,x,sizeof(a))
#define inf (1<<29)
using namespace std;
typedef long long ll;
const int N = 22;
const int dx[4] = {-1,1,0,0};
const int dy[4] = {0,0,-1,1};
bool vis[N][N][(1<<14)];
bool mp[N][N];
int dis[3][3];
inline void init()
{
dis[0][1] = 0;
dis[2][1] = 3;
dis[1][2] = 1;
dis[1][0] = 2;
}
int n,m,l;
struct snack
{
int x[10],y[10],t;
int s;//四进制数表示蛇身的状态
}h;
bool ok(int x,int y,snack ss)
{
if (mp[x][y]) return 0;//石头
for (int i = 1;i <= l;++i)
{
if (x==ss.x[i]&&y==ss.y[i]) return 0;//蛇身
}
return 1;
}
void update(snack &nx,snack h)
{
for (int i = 2;i <= l;++i)
{
nx.x[i] = h.x[i-1];
nx.y[i] = h.y[i-1];
}
}
int fun(snack ss,int k)
{
int ans = 0;
for (int i = l-1;i > 1;--i)
{
ans = ans*4 + dis[ ss.x[i] - ss.x[i-1] + 1 ][ ss.y[i] - ss.y[i-1] + 1 ] ;
}
ans = ans*4 + dis[1-dx[k]][1-dy[k]];
return ans;
}
int bfs()
{
queue<snack>q;
q.push(h);mem(vis,0);vis[h.x[1]][h.y[1]][h.s] = 1;
while (!q.empty())
{
h = q.front();q.pop();
if (h.x[1]==1&&h.y[1]==1) return h.t;
for (int i = 0;i < 4;++i)
{
snack nx = h;
nx.x[1] += dx[i];
nx.y[1] += dy[i];
++nx.t ;
if (!ok(nx.x[1],nx.y[1],h)) continue;
if (nx.x[1]>=1&&nx.y[1]>=1&&nx.x[1]<=n&&nx.y[1]<=m)
{
if (nx.x[1]==1&&nx.y[1]==1) return nx.t;
update(nx,h);//更新蛇身
nx.s = fun(nx,i);//转换成四进制数
bool &vist = vis[nx.x[1]][nx.y[1]][nx.s];
if (vist) continue;
q.push(nx);
vist = 1;
}
}
}
return -1;
}
int main()
{
int kas = 0;init();
while (~scanf("%d %d %d",&n,&m,&l))
{
if (n==0&&m==0&&l==0) break;
for (int i = 1;i <= l;++i) scanf("%d %d",&h.x[i],&h.y[i]);
int k;scanf("%d",&k);mem(mp,0);
for (int i = 0,x,y;i < k;++i)
{
scanf("%d %d",&x,&y);
mp[x][y] = 1;
}
int ans = 0;
for (int i = l;i > 1;--i)
{
ans = ans*4 + dis[ h.x[i] - h.x[i-1] + 1 ][ h.y[i] - h.y[i-1] + 1 ] ;
}
h.s = ans;
h.t = 0;
printf("Case %d: %d\n",++kas,bfs());
}
return 0;
}