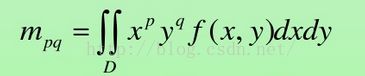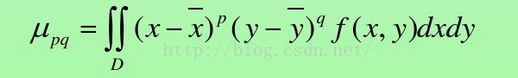【图像处理入门】之 不变矩与Harris算子(未完待续)
本文为个人入门摘录总结,如有错误请包涵
后续还会加入相应图像代码,因为只是字面上理解,应该存在很多的偏差
比如说Hu矩的基于直角坐标系是指规格化吗?
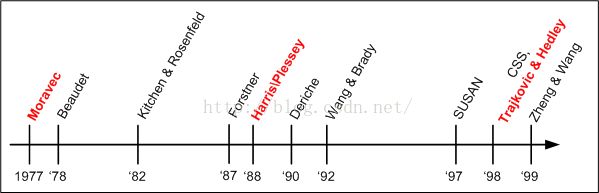
不变矩(目前只大致学习了经典矩)相关Review如下图
不变矩
简述不变矩及无偏估计与有偏估计
设A'=g(X1,X2,...,Xn)是未知参数A的一个点估计量,若A'满足
E(A')= A
则称A'为A的无偏估计量,否则为有偏估计量
矩的定义
Hu矩
Zernike矩
Zernike矩为基于Zernike多项式的正交化函数,所利用的正交多项式集(完备性是指在数学及其相关领域中,当一个对象具有完备性,即它不需要添加任何其他元素,这个对象也可称为完备的或完全的。 正交的完备性在线性空间中就是指构成这个空间的基是相互正交的,即这个空间中所有的向量都可以由这组基线性表出,而且这些基又相互正交.)Zernike矩源自于Teague提出的正交矩思想,相较于Hu矩,其具备良好的旋转不变性,作为正交矩能够构造任意的高阶矩,运算为积分运算,因此对噪声不敏感。
当计算一幅图像的Zernike矩时,以该图像的形心(也称为原点)把像素坐标映射到单位圆内
Zernike矩是图像函数f(x,y)在正交多项式上的投影,其中正交多项式在单位圆内正交
Zernike矩提取方案为:
Zernike矩与Hu矩及其应用
1)优点:
不变矩不受旋转以及大小的影响,可以将其应用于识别二维或者三维物体。
2)缺点:
①不变矩对噪声很敏感,因此有其他作者提出相关不变矩对上述进行改进。
②矩计算时间比较长。
③矩是一种整体性质,如果物体的一部分被其他物体遮挡,则无法计算不变矩。比如说角点是一种描述局部的性质
④Hu提出的不变矩只能对区域进行检测,不能用于边界的检测;对于区域的检测,总体上来说,极半径不变矩与Hu矩的效果相当;但是Hu矩收到图形对称性的影响,而极半径不变矩不受到图形对称性的影响,所以对于对称图形来说,极半径不变矩的效果要优于Hu不变矩
3)应用:
Hu和Zernike矩都具备平移旋转以及缩放的不变性,但是各有特点。Hu的目标信息不是很全面,含有较多的冗余信息;Zernike矩是正交矩,能够构造出任意的高阶矩,包含信息全面,对噪声不敏感。可采用不变矩应用于人形识别算法。
Harris角点检测
角点检测基础
图像变化类型:
有几何变换和灰度变换。
几何变换又可以分为旋转,仿射(非各项同性的缩放)以及相似(各项同性的缩放)
特征点提取的作用:
是许多计算机视觉算法的基础——使用特征点来代表图像的内容
运动目标跟踪
物体识别
图像配准
全景图像拼接
三维重建
角点的定义以及发展:
角点:
最直观的印象就是在水平、竖直两个方向上变化均较大的点,即Ix、Iy都较大
边缘:仅在水平、或者仅在竖直方向有较大的变化量,即Ix和Iy只有其一较大
平坦地区:在水平、竖直方向的变化量均较小,即Ix、Iy都较小
好的角点算法定义:
检测出图像中“真实的”角点准确的定位性能
很高的重复检测率(稳定性好)
具有对噪声的鲁棒性
具有较高的计算效率
角点算法的发展:典型的角点检测算法有Harris算法以及CSS算法
其中Harris算法由Chris Harris和Mike Stephens于1988年在A COMBINED CORNER AND EDGE DETECTOR一文中提出
Harris角点算法思想以及实现
Harris角点算法思想:
由局部小窗口观察图像特征,角点定义:窗口向任意方向的移动都导致图像灰度的明显变化
Harris角点性质:
更多角点评价:Evaluation of Interest Point Detectors(IJCV 2000)
具备旋转不变性(椭圆转过一定角度,但是其形状保持不变,即特征值保持不变,角点响应函数R对于图像的旋转具备不变性)
对于图像灰度的仿射变化具备部分的不变性(只使用了图像导数,对于灰度平移变化不变,对于图像灰度的尺度变化)
对于尺度变换不具备不变性
Harris角点的实现:定义了灰度变化函数(窗函数*灰度平移前后变化差的平方)以及角点响应函数R
灰度平移前后变化差可以进行泰勒展开,取二阶导及以后项为极小项,相减后即可以得到一个窗口响应函数,根据窗口响应函数分布根据窗口响应函数可以定义角点响应函数R=det M - k(trace M)²【这块的推导应该进行相关研究。 对角点响应函数的理解?】
算法:首先对角点响应函数R进行阈值处理(R>threshold)然后提取R的局部极大值