UFLDL教程答案(4):Exercise:Softmax Regression

教程地址：http://deeplearning.stanford.edu/wiki/index.php/Exercise:Softmax_Regression

练习地址：http://deeplearning.stanford.edu/wiki/index.php/Softmax%E5%9B%9E%E5%BD%92

1.几个要点

(1)参数冗余：

        如果参数 是代价函数 的极小值点，那么 同样也是它的极小值点，其中 可以为任意向量。因此使 最小化的解不是唯一的。（有趣的是，由于 仍然是一个凸函数，因此梯度下降时不会遇到局部最优解的问题。但是 Hessian 矩阵是奇异的/不可逆的，这会直接导致采用牛顿法优化就遇到数值计算的问题）。

        在实际应用中，为了使算法实现更简单清楚，往往保留所有参数 ，而不任意地将某一参数设置为 0。但此时我们需要对代价函数做一个改动：加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。

 

(2)核心公式：

公式(1)：计算cost

公式(2)：计算梯度（UFLDL教程答案(6)中有详细推导）

公式(3)：

 

(3)Implementation Tip:

(a)ground truth matrix的作用是实现公式中的函数 值为真的表达式

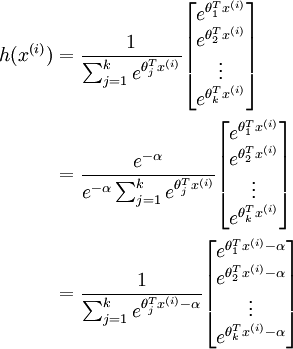
(b)指数函数可能非常大导致溢出，由下面公式，解决办法是都减去一个常数α，α可以取(j=1，2，....，10)中的最大值。注意10代表0，loaddata的时候对label进行了修改，目的是便于代码实现。

若M(r, c) is ，代码为：

% M is the matrix as described in the text
M = bsxfun(@minus, M, max(M, [], 1));%max(M,[],1)取M中各列最大元素，结果为一个行向量；max(M,[],2)为各行最大元素

(c) bsxfun

和repmat功能差不多，这个更有效率。

>> a = [1;2;3]

a =                                       

     1
     2
     3

>> b = bsxfun(@times,a,[1 2 4])

b =

     1     2     4
     2     4     8
     3     6    12

 

矩阵a为1列，b为3列，把扩展到3列；b为1行，a为3行，把扩展到3行；然后b=a.*b

a =                                       

     1     1     1
     2     2     2
     3     3     3

b =

     1     2     4
     1     2     4
     1     2     4

 

(d)梯度检验：

设定了一个DEBUG变量，为true时，不会用真实数据集，而是用randn，randi随机产生数据和类别，来检查梯度函数是否正确。

 

(e)一些调试过程的错误：

注意：教程压缩包代码里 images = loadMNISTImages('mnist/train-images-idx3-ubyte');  所以注意你的数据文件的路径；

           而且train-images-idx3-ubyte应该是train-images-.dx3-ubyte'

           DEBUG的时候运行到test部分会出错，是因为DEBUG时数据是8*100，实际test是784*10000。

2.进入正题

1.Step 2: Implement softmaxCost

M=theta*data;
M = bsxfun(@minus, M, max(M, [], 1));
%max(M,[],1)取M中各列最大元素，结果为一个行向量；max(M,[],2)为各行最大元素
M=exp(M);
H = bsxfun(@rdivide, M, sum(M));  %归一化公式3
M=log(H);
M=M.*groundTruth;
cost=-1/numCases*sum(sum(M,1),2)+ lambda/2 * sum(sum(theta.^2));  %公式1
thetagrad=-1/numCases*(groundTruth-H)*data'+lambda * theta;  %公式2

2.Step 5: Testing（softmaxPredict.m）

theta_x=theta * data;
[m, pred] = max(theta_x);
%只需要比较哪类概率大，由公式3可知，只用计算theta * data部分即可

 

3.实验结果

结果如图，可以看到，正确率达到了92.640%