HDU 3338 Kakuro Extension 网络流

题意：

题意就是要求在白色方格内填1-9的数字，使得一行连续白块的和等于左边第一个黑色方格右上角的值，每一列连续白块的和等于上方第一个黑色方格左下的值，题目保证第一行和第一列为黑色，且保证有解。

解题思路：

建立源点和汇点，从s向左下有值黑色方块建容量为该值的边，从右上有值的边向汇点t建立容量为该值的边，对于白块建一条左边第一黑色方块指向它的边，再建一条它指向上方第一黑块的边。但是用网络流这样得到的结果并不是答案，因为白块中的点只能填1-9的数字。也就是说，与白块相连的边的容量c（e）要求,$1<=c(e)<=9$,怎么限制最低流量呢？

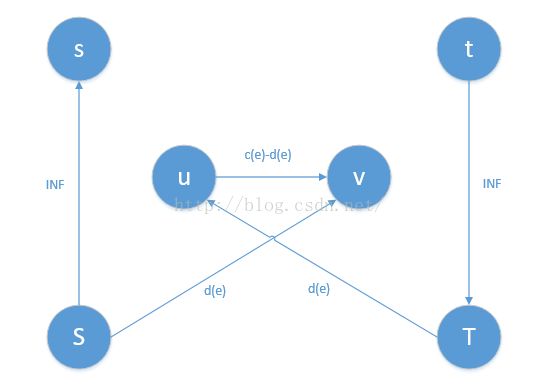
建立新的源点和汇点S,T,对任意有最低流量限制的边e(u,v){d(e)<=f(e)<=c(e)}，设e的容量设置为c(e)-d(e),再从S建一条容量为d(e)指向v的边，从u建一条容量为d(e)指向T的边,

最后从S建一条流量为INF指向s的边，从t建一条容量为INF指向T的边。如图：

从新的源点到汇点的最大流就是结果。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<map>
#include<string>
#include<queue>
#include<vector>
#include<list>
//#pragma comment(linker,"/STACK:1024000000,1024000000")
using namespace std;
#define INF 0x3f3f3f3f
#define MAX_V 20010
struct edge{int to,cap,rev;};
int V;
vector<edge> G[MAX_V];
int prevv[MAX_V],preve[MAX_V];
int num[MAX_V],iter[MAX_V],level[MAX_V];

int n,m;
void add_edge(int from,int to,int cap)
{
    G[from].push_back( (edge){to,cap,G[to].size()}  );
    G[to].push_back( (edge){from,0,G[from].size()-1} );
}
void bfs(int t)
{
    memset(num,0,sizeof num);
    memset(level,-1,sizeof level);
    level[t]=0;num[0]++;
    queue<int> que;
    que.push(t);
    while(!que.empty())
    {
        int u=que.front();que.pop();
//        cout<<u<<endl;
        for(int i=0;i<G[u].size();i++)
        {
            edge e=G[u][i];
            edge rev=G[e.to][e.rev];
            if(rev.cap>0&&level[e.to]<0)
            {
                level[e.to]=level[u]+1;
                num[level[e.to]]++;
                que.push(e.to);
            }
        }
    }
}
int augment(int s,int t)
{
    int f=INF;
    for(int v=t;v!=s;v=prevv[v])
    {
        edge e=G[prevv[v]][preve[v]];
        f=min(f,e.cap);
    }
    for(int v=t;v!=s;v=prevv[v])
    {
        edge &e=G[prevv[v]][preve[v]];
        e.cap-=f;
        G[e.to][e.rev].cap+=f;
    }
    return f;
}
int max_flow(int s,int t)
{
    int u,flow=0;
    memset(iter,0,sizeof iter);
    u=s;
    bfs(t);
    while(level[u]<V)
    {
        if(u==t)
        {
            flow+=augment(s,t);
            u=s;
        }
        int is=0;
        for(int &i=iter[u];i<G[u].size();i++)
        {
            edge e=G[u][i];
            if(e.cap>0&&level[u]==level[e.to]+1)
            {
                prevv[e.to]=u;
                preve[e.to]=i;
                u=e.to;
                is=1;break;
            }
        }
        if(!is)
        {
            int Min=V-1;
            for(int i=0;i<G[u].size();i++)
            {
                edge e=G[u][i];
                if(e.cap>0) Min=min(Min,level[e.to]);
            }
            if(--num[level[u]]==0) break;
            num[level[u]=Min+1]++;
            iter[u]=0;
            if(u!=s) u=prevv[u];
        }
    }
    return flow;
}
char mp[105][105][8];
int ll[105][105],uu[105][105];
int main()
{
    while(~scanf("%d %d",&n,&m))
    {
        for(int i=0;i<MAX_V;i++) G[i].clear();
        int s=n*m*2,t=s+1;
        int S=n*m*2+2,T=S+1;
        V=n*m*2+4;
        memset(ll,-1,sizeof ll);
        memset(uu,-1,sizeof uu);
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
            scanf("%s",mp[i][j]);
        add_edge(S,s,INF);
        add_edge(t,T,INF);
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
        {
            if(strcmp(mp[i][j],".......")==0)
            {
                ll[i][j]=ll[i][j-1];
                uu[i][j]=uu[i-1][j];
                add_edge(2*(i*m+ll[i][j]),2*(i*m+j),8);
                add_edge(S,2*(i*m+j),1);
                add_edge(2*(i*m+ll[i][j]),T,1);
                add_edge(2*(i*m+j),2*(uu[i][j]*m+j)+1,9);
            }
            else
            {
                ll[i][j]=j;
                uu[i][j]=i;
                int cap=0;
                for(int k=0;k<3;k++)
                    if(mp[i][j][k]=='X') break;
                    else cap=cap*10+mp[i][j][k]-'0';
                if(cap) add_edge(2*(i*m+j)+1,t,cap);

                cap=0;
                for(int k=4;k<7;k++)
                    if(mp[i][j][k]=='X') break;
                    else cap=cap*10+mp[i][j][k]-'0';
                if(cap) add_edge(s,2*(i*m+j),cap);

            }
        }
        int flow=max_flow(S,T);
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
        {
            if(strcmp(mp[i][j],".......")==0)
            {
                edge e=G[2*(i*m+j)][0];
                edge e2=G[2*(i*m+j)][1];
                printf("%d",e.cap+e2.cap);
            }
            else printf("_");
            if(j==m-1) printf("\n");
            else printf(" ");
        }
    }
    return 0;
}