| (2)本文简介
作为系列第一篇,本文介绍最简单的运动学模拟,只有两条非常简单的公式。运动学模拟可以用来模拟很多物体运动(例如马里奥的跳跃、炮弹等),本文将会配合粒子系统做出一些视觉特效(粒子系统其实也可以用来做游戏的玩法,而不单是视觉特效)。
(3)运动学模拟
运动学(kinematics)研究物体的移动,和动力学(dynamics)不同之处,在于运动学不考虑物体的质量(mass)/转动惯量(moment of inertia),以及不考虑加之于物体的力(force )和力矩(torque)。 我们先回忆牛顿第一运动定律:
当物体不受外力作用,或所受合力为零时,原先静止者恒静止,原先运动者恒沿着直线作等速度运动。该定律又称为「惯性定律」。
此定律指出,每个物体除了其位置(position)外,还有一个线性速度(linear velocity)的状态。然而,只模拟不受力影响的物体并不有趣。撇开力的概念,我们可以用线性加速度(linear acceleration)去影响物体的运动。例如,要计算一个自由落体在任意时间t的y轴座标,可以使用以下的分析解(analytical solution): 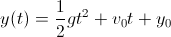

欧拉方法非常简单,但有准确度和稳定性问题,本文会先忽略这些问题。本文的例子采用二维空间,我们先实现一个JavaScript二维矢量类:
// Vector2.js
Vector2 = function(x, y) { this.x = x; this.y = y; };
Vector2.prototype = {
copy : function() { return new Vector2(this.x, this.y); },
length : function() { return Math.sqrt(this.x * this.x + this.y * this.y); },
sqrLength : function() { return this.x * this.x + this.y * this.y; },
normalize : function() {
var inv = 1/this.length();
return new Vector2(this.x * inv, this.y * inv);
},
negate : function() { return new Vector2(-this.x, -this.y); },
add : function(v) { return new Vector2(this.x + v.x, this.y + v.y); },
subtract : function(v) { return new Vector2(this.x - v.x, this.y - v.y); },
multiply : function(f) { return new Vector2(this.x * f, this.y * f); },
divide : function(f) { var invf = 1/f; return new Vector2(this.x * invf, this.y * invf); },
dot : function(v) { return this.x * v.x + this.y * v.y; }
};
Vector2.zero = new Vector2(0, 0);
然后,就可以用HTML5 Canvas去描绘模拟的过程:
<html><head><title>Kinematics</title></head>
<body>
<script type="text/javascript" src="Framework.js"></script>
<script type="text/javascript" src="Vector2.js"></script>
<textarea id="code" rows="20" cols="100">
var position = new Vector2(10, 200);
var velocity = new Vector2(50, -50);
var acceleration = new Vector2(0, 10);
var dt = 0.1; function step() {
position = position.add(velocity.multiply(dt));
velocity = velocity.add(acceleration.multiply(dt)); ctx.strokeStyle = "#000000";
ctx.fillStyle = "#FFFFFF";
ctx.beginPath();
ctx.arc(position.x, position.y, 5, 0, Math.PI*2, true);
ctx.closePath();
ctx.fill();
ctx.stroke();
}
start("kinematicsCancas", step);
</textarea>
<br />
<button onclick="eval(document.getElementById('code').value)">Run</button>
<button onclick="stop();">Stop</button>
<button onclick="clearCanvas();">Clear</button>
<br />
<canvas id="kinematicsCancas" width="400" height="400"></canvas>
</body>
</html>
点击观看效果
 改代码试试看:改变起始位置, 改变起始速度(包括方向),改变加速度。
这程序的核心就是step()函数头两行代码。很简单吧? (4)粒子系统
粒子系统(particle system)是图形里常用的特效。粒子系统可应用运动学模拟来做到很多不同的效果。粒子系统在游戏和动画中,常常会用来做雨点、火花、烟、爆炸等等不同的视觉效果。有时候,也会做出一些游戏性相关的功能,例如敌人被打败后会发出一些闪光,主角可以把它们吸收。 4.1 粒子的定义
粒子系统模拟大量的粒子,并通常用某些方法把粒子渲染。粒子通常有以下特性:
1.粒子是独立的,粒子之间互不影响(不碰撞、没有力)
2.粒子有生命周期,生命结束后会消失
3.粒子可以理解为空间的一个点,有时候也可以设定半径作为球体和环境碰撞
4.粒子带有运动状态,也有其他外观状态(例如颜色、影像等)
5.粒子可以只有线性运动,而不考虑旋转运动(也有例外)
以下是本文例子里实现的粒子类:
/*
* @requires Vector2, Color
*/
Particle = function(position, velocity, life, color, size) {
this.position = position;
this.velocity = velocity;
this.acceleration = Vector2.zero;
this.age = 0;
this.life = life;
this.color = color;
this.size = size;
};
4.2 游戏循环 粒子系统通常可分为三个周期:
1.发射粒子
2.模拟粒子(粒子老化、碰撞、运动学模拟等等)
3.渲染粒子
在游戏循环(game loop)中,需要对每个粒子系统执行以上的三个步骤。
4.3 生与死
在本文的例子里,用一个JavaScript数组particles储存所有活的粒子。产生一个粒子只是把它加到数组末端。代码片段如下: /ParticleSystem.js
function ParticleSystem() {
// Private fields
var that = this;
var particles = new Array();
// Public fields
this.gravity = new Vector2(0, 100);
this.effectors = new Array();
// Public methods
this.emit = function(particle) {
particles.push(particle);
};
// ...
}
粒子在初始化时,年龄(age)设为零,生命(life)则是固定的。年龄和生命的单位都是秒。每个模拟步,都会把粒子老化,即是把年龄增加,年龄超过生命,就会死亡。代码片段如下:
function ParticleSystem() {
// ...
this.simulate = function(dt) {
aging(dt);
applyGravity();
applyEffectors();
kinematics(dt);
};
// ...
// Private methods
function aging(dt) {
for (var i = 0; i < particles.length; ) {
var p = particles[i];
p.age += dt;
if (p.age >= p.life)
kill(i);
else
i++;
}
}
function kill(index) {
if (particles.length > 1)
particles[index] = particles[particles.length - 1];
particles.pop();
}
// ...
} 在函数kill()里,用了一个技巧。因为粒子在数组里的次序并不重要,要删除中间一个粒子,只需要复制最末的粒子到那个元素,并用pop()移除最末的粒子就可以。这通常比直接删除数组中间的元素快(在C++中使用数组或std::vector亦是)。
4.4 运动学模拟
把本文最重要的两句运动学模拟代码套用至所有粒子就可以。另外,每次模拟会先把引力加速度写入粒子的加速度。这样做是为了将来可以每次改变加速度(续篇会谈这方面)。
function ParticleSystem() {
// ...
function applyGravity() {
for (var i in particles)
particles[i].acceleration = that.gravity;
}
function kinematics(dt) {
for (var i in particles) {
var p = particles[i];
p.position = p.position.add(p.velocity.multiply(dt));
p.velocity = p.velocity.add(p.acceleration.multiply(dt));
}
}
// ...
}
4.5 渲染
粒子可以用很多不同方式渲染,例如用圆形、线段(当前位置和之前位置)、影像、精灵等等。本文采用圆形,并按年龄生命比来控制圆形的透明度,代码片段如下: function ParticleSystem() {
// ...
this.render = function(ctx) {
for (var i in particles) {
var p = particles[i];
var alpha = 1 - p.age / p.life;
ctx.fillStyle = "rgba("
+ Math.floor(p.color.r * 255) + ","
+ Math.floor(p.color.g * 255) + ","
+ Math.floor(p.color.b * 255) + ","
+ alpha.toFixed(2) + ")";
ctx.beginPath();
ctx.arc(p.position.x, p.position.y, p.size, 0, Math.PI * 2, true);
ctx.closePath();
ctx.fill();
}
}
// ...
} 4.6 基本粒子系统完成
以下的例子里,每帧会发射一个粒子,其位置在画布中间(200,200),发射方向是360度,速率为100,生命为1秒,红色、半径为5象素。
<html><head><title>Basic Particle System</title></head>
<body>
<script type="text/javascript" src="Framework.js"></script>
<script type="text/javascript" src="Vector2.js"></script>
<script type="text/javascript" src="Color.js"></script>
<script type="text/javascript" src="Particle.js"></script>
<script type="text/javascript" src="ParticleSystem.js"></script>
<textarea id="code" rows="20" cols="100">
var ps = new ParticleSystem();
var dt = 0.01; function sampleDirection() {
var theta = Math.random() * 2 * Math.PI;
return new Vector2(Math.cos(theta), Math.sin(theta));
} function step() {
ps.emit(new Particle(new Vector2(200, 200), sampleDirection().multiply(100), 1, Color.red, 5));
ps.simulate(dt); clearCanvas();
ps.render(ctx);
} start("basicParticleSystemCanvas", step);
</textarea>
<br />
<button onclick="eval(document.getElementById('code').value)">Run</button>
<button onclick="stop();">Stop</button>
<br />
<canvas id="basicParticleSystemCanvas" width="400" height="400"></canvas>
</body>
</html>
点击看效果。
修改代码试试看。改变发射位置,向上发射,发射范围在90度内,改变生命,改变半径,每帧发射5个粒子
(5)简单碰撞
为了说明用数值积分相对于分析解的优点,本文在粒子系统上加简单的碰撞。我们想加入一个需求,当粒子碰到长方形室(可设为整个Canvas大小)的内壁,就会碰撞反弹,碰撞是完全弹性的(perfectly elastic collision)。 在程序设计上,我把这功能用回调方式进行。 ParticleSystem类有一个effectors数组,在进行运动学模拟之前,先执行每个effectors对象的apply()函数: 而长方形室就这样实现:
// ChamberBox.js
function ChamberBox(x1, y1, x2, y2) {
this.apply = function(particle) {
if (particle.position.x - particle.size < x1 || particle.position.x + particle.size > x2)
particle.velocity.x = -particle.velocity.x;
if (particle.position.y - particle.size < y1 || particle.position.y + particle.size > y2)
particle.velocity.y = -particle.velocity.y;
};
}
这其实就是当侦测到粒子超出内壁的范围,就反转该方向的速度分量。
此外,这例子的主循环不再每次把整个Canvas清空,而是每帧画一个半透明的黑色长方形,就可以模拟动态模糊(motion blur)的效果。粒子的颜色也是随机从两个颜色中取样。(源码请下载)
点击看效果。
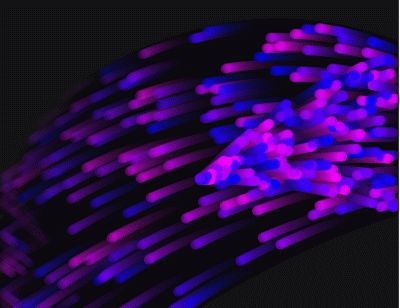
(6)互动发射
最后一个例子加入互动功能,在鼠标位置发射粒子,粒子方向是按鼠标移动速度再加上一点噪音(noise)。粒子的大小和生命都加入了随机性。点击看效果。
(7)总结
本文介绍了最简单的运动学模拟,使用欧拉方法作数值积分,并以此法去实现一个有简单碰撞的粒子系统。本文的精华其实只有两条简单公式(只有两个加数 和两个乘数),希望让读者明白,其实物理模拟可以很简单。虽然本文的例子是在二维空间,但这例子能扩展至三维空间,只须把Vector2换成 Vector3。本文完整源代码可下载。 |