hdu 5375 Gray code (DP)

题目链接

Problem Description

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only onebit (binary digit). The reflected binary code was originally designed to prevent spurious output from electromechanical switches. Today, Gray codes are widely used to facilitate error correction in digital communications such as digital terrestrial television and some cable TV systems.



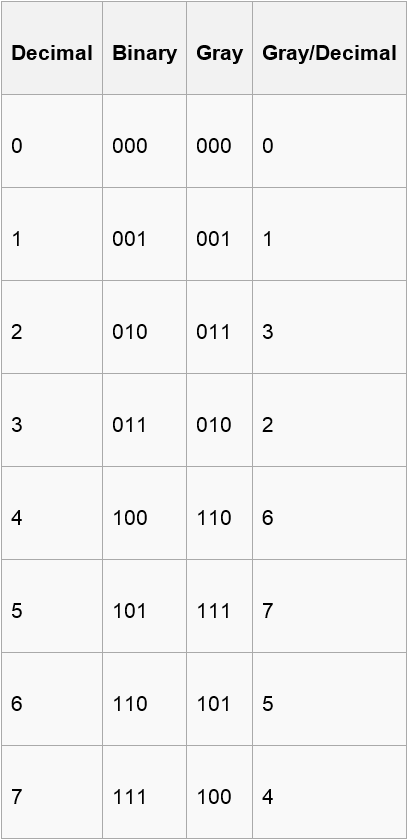
Now , you are given a binary number of length n including ‘0’ , ’1’ and ‘?’(? means that you can use either 0 or 1 to fill this position) and n integers(a1,a2,….,an) . A certain binary number corresponds to a gray code only. If the ith bit of this gray code is 1,you can get the point ai.
Can you tell me how many points you can get at most?

For instance, the binary number “00?0” may be “0000” or “0010”,and the corresponding gray code are “0000” or “0011”.You can choose “0000” getting nothing or “0011” getting the point a3 and a4.

 

Input

The first line of the input contains the number of test cases T.

Each test case begins with string with ‘0’,’1’ and ‘?’.

The next line contains n (1<=n<=200000) integers (n is the length of the string).

a1 a2 a3 … an (1<=ai<=1000)

 

Output

For each test case, output “Case #x: ans”, in which x is the case number counted from one,’ans’ is the points you can get at most

 

Sample Input

   
   
   
   

    
    
    
    2
00?0
1 2 4 8
????
1 2 4 8
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case #1: 12
Case #2: 15

   
   
   
   
题意：给你一串字符，只包括0，1和？，问号代表此处可以是0，可以是1，可以知道字符串长度为n,这串二进制可以转换为格雷码表示，二进制到格雷码之间转换关系为：首先在前面添个0，然后两两异或得到n个数。题目中再给你n正整数，a[i]代表如果格雷码第i位为1 ，则可以得到a[i]的值，问你最大值（就是如何分配问号的值使得到的值最大）。
这是一个明显的DP题，虽然要转换为格雷码才可以，但是我们没必要先转换出来，直接对原串操作即可，判断当前点和前面一个点的关系就可以转移状态，我们用dp[i][j] (0<=i<n,j=0,1)表示第i个位置为j时取得的最大值，想一想，如果第i处为1或者0，那么转移时此处就只能转移1或者0的状态，而当此处为？时，因为问号可以为1或者0，因此都要转移，取max即可。
代码如下：
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
int dp[200005][2];
char s[200005];
int a[200005];
int main()
{
    int t;
    scanf("%d",&t);
    for(int ca=1;ca<=t;ca++)
    {
        scanf("%s",s);
        int n=strlen(s);
        for(int i=0;i<n;i++) scanf("%d",&a[i]);
        memset(dp,0,sizeof(dp));
        if(s[0]=='1') dp[0][1]=a[0];
        else if(s[0]=='?') dp[0][1]=a[0];
        for(int i=1;i<n;i++)
        {
            if(s[i]=='0')//只有0可以转移
            {
                dp[i][0]+=dp[i-1][0];//如果下面这个if条件不满足，那么上一个为0的状态还是要转移过来
                if(s[i-1]=='1'||s[i-1]=='?') dp[i][0]=max(dp[i][0],dp[i-1][1]+a[i]);
            }
            else if(s[i]=='1')//只有1可以转移
            {
                dp[i][1]+=dp[i-1][1];
                if(s[i-1]=='0'||s[i-1]=='?') dp[i][1]=max(dp[i][1],dp[i-1][0]+a[i]);
            }
            else if(s[i]=='?')//0和1都可以转移
            {
                dp[i][0]+=dp[i-1][0];
                dp[i][1]+=dp[i-1][1];
                if(s[i-1]=='1'||s[i-1]=='?') dp[i][0]=max(dp[i][0],dp[i-1][1]+a[i]);
                if(s[i-1]=='0'||s[i-1]=='?') dp[i][1]=max(dp[i][1],dp[i-1][0]+a[i]);
            }
        }
        printf("Case #%d: %d\n",ca,max(dp[n-1][0],dp[n-1][1]));
    }
    return 0;
}