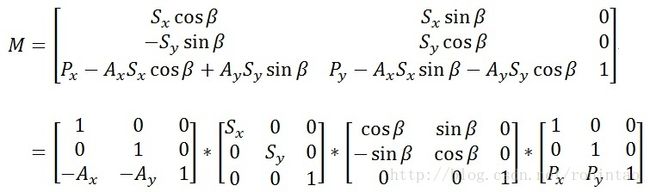【cocos2D-x学习】5.坐标系其三——再看Cocos中的坐标系

【目标】学习cocos-2Dx 中的坐标系

 

【参考】：

《中文文档- Cocos2D-X中文站》  http://cocos2d.cocoachina.com/document

《【cocos2d-x官方文档】cocos2d-x坐标系详解》  http://www.ityran.com/archives/3367

《Cocos-2d 坐标系及其坐标转换》  http://blog.csdn.net/tskyfree/article/details/8292544

 《CGAffineTransform Reference》  https://developer.apple.com/library/mac/#documentation/graphicsimaging/reference/CGAffineTransform/Reference/reference.html

 

一、入手的简单例子

          这里仅讨论设置位置的坐标系，TILE地图坐标系、触屏坐标系等不在讨论范围之内。

          先看一段HelloWorld的代码：

        CCSprite* pSprite = CCSprite::create("HelloWorld.png");
        CC_BREAK_IF(! pSprite);

        // Place the sprite on the center of the screen
        pSprite->setPosition(ccp(size.width/2, size.height/2));

        // Add the sprite to HelloWorld layer as a child layer.
        this->addChild(pSprite, 0);

        这段代码是在 HelloWorld 的 init 中的代码，其中 HelloWorld 是一个 CCLayer，HelloWorld.png是一张和屏幕大小(480 * 320)一样的图片，最终显示的效果是这张图片恰好占据了整个屏幕的大小，显示出来。我们就从这里开始。

1、源：图片

        首先我们有一张图片，HelloWorld.png，480 * 320，这个是实际上要显示的内容的真正来源，对于坐标系的研究而言，最核心的关心，是这张图片上的某个点 (x, y)，最后映射到屏幕的什么位置。

2、子节点 -》 父节点

        接下来是pSprite，它是CCSprite的对象，是一个节点。在这段代码中，pSprite通过加载HelloWorld.png，获得了展示的内容纹理，在CCSprite中可以看到，他实际上就是通过 ccGLBindTexture2D 将纹理绘制了出来，并且将自己的内容区域设置成纹理的大小。

        但pSprite并不是我们所想要显示的全部，他只是整个界面的一部分，被加载进父节点helloWorld中。这个动作是由addChild完成的，而具体摆放在父节点的什么位置呢？pSprite 设置了自己的位置 setPosition。不过注意到这个setPosition是在 addChild之前，也就是说，pSprite在还不知道自己的父亲在什么地方的时候，就已经设置好自己的位置了。因此可以猜测，这个Position是与父节点相对独立的。

3、根节点 -》 世界

      HelloWorld这个根节点在加载了所有的子布局之后，对他而言，已经没有父节点了，那么就需要把自己显示在屏幕上，这一步的变换就是从自己的坐标系映射向屏幕。不过在cocos之中，目前我还没有看到类似于 glFrustum 这样的透视裁剪设置（毕竟移动设备总是全屏显示的），所以实际上世界坐标系到屏幕坐标系的映射基本是固定的，这里就合一了。

4、对流程的总结

      子节点坐标系           ->     父节点坐标系             ->         …………      ->    根节点的坐标系          ->     世界坐标系

      在节点中的位置               在父节点中的位置                                                在根节点中的位置               在世界中的位置

二、从CCNode分析坐标系的变换

1、齐次变换矩阵 CCAffineTransform

       根据从OpenGL中的经验可以知道，坐标系的切换的核心，就是变换矩阵。在cocos中，有个类是专门用来表示这样的矩阵的，就是 CCAffineTransform。由于cocos2D是一个二维引擎，所以坐标是二维的，那么齐次变换矩阵就应该是3*3的，所以  CCAffineTransform 的矩阵如下（函数可见  __CCAffineTransformMake() ）：

     （式2-1）

       需要注意的是这个矩阵和《4.坐标系其二——OpenGL中的坐标系》中的变换矩阵的表示方式不同，两者成转置关系，所以这里的矩阵是右乘坐标点的（函数代码可见  __CCPointApplyAffineTransform(const CCPoint& point, const CCAffineTransform& t)  ）：

         （式2-2）

       【这个类，我有一个地方没有弄明白，就是  CCAffineTransformTranslate  这个函数实际上是左乘了位移矩阵，转置之后，就相当于在第四节中的齐次矩阵右乘了位移矩阵，相当于先进行位移，再进行剩余变换，不过幸好我们这里不需要涉及到这个方法】

2、节点的变换矩阵 nodeToParentTransform

       对于子节点中的坐标(x, y) ，到父节点坐标系中的位置 (x', y') ，这个变换矩阵，在CCNode 中，是用 nodeToParentTransform 来获取的。这就是一个  CCAffineTransform 矩阵，那么里面的值到底是多少呢？我们可以具体看代码：

CCAffineTransform CCNode::nodeToParentTransform(void)
{
    if (m_bIsTransformDirty) 
    {

        // Translate values
        float x = m_tPosition.x;
        float y = m_tPosition.y;

        if (m_bIgnoreAnchorPointForPosition) 
        {
            x += m_tAnchorPointInPoints.x;
            y += m_tAnchorPointInPoints.y;
        }

        // Rotation values
        float c = 1, s = 0;
        if (m_fRotation) 
        {
            float radians = -CC_DEGREES_TO_RADIANS(m_fRotation);
            c = cosf(radians);
            s = sinf(radians);
        }

        bool needsSkewMatrix = ( m_fSkewX || m_fSkewY );


        // optimization:
        // inline anchor point calculation if skew is not needed
        if (! needsSkewMatrix && !m_tAnchorPointInPoints.equals(CCPointZero))
        {
            x += c * -m_tAnchorPointInPoints.x * m_fScaleX + -s * -m_tAnchorPointInPoints.y * m_fScaleY;
            y += s * -m_tAnchorPointInPoints.x * m_fScaleX +  c * -m_tAnchorPointInPoints.y * m_fScaleY;
        }


        // Build Transform Matrix
        m_tTransform = CCAffineTransformMake( c * m_fScaleX,  s * m_fScaleX,
            -s * m_fScaleY, c * m_fScaleY,
            x, y );

        // XXX: Try to inline skew
        // If skew is needed, apply skew and then anchor point
        if (needsSkewMatrix) 
        {
             ......// skew 这一段没有研究，因为暂时还用不到这个变换
        }

        m_bIsTransformDirty = false;
    }

    return m_tTransform;
}

       代码本身并没有难解之处，现在假定设定的Position是 (Px, Py)，锚点是 (Ax, Ay)，旋转的角度是β°，缩放的比例是(Sx, Sy)，needsSkewMatrix = false，对于CCSprite来说m_bIgnoreAnchorPointForPosition = false，（Layer中是true）。那么生成的矩阵是

     （式2-3）

      注意我这里把这个矩阵分解成了四个矩阵相乘，下面来看看这样做的道理。不过这里涉及到锚点，那么先对这个概念加以评述。

3、锚点

        锚点的坐标是未变换前的坐标系下的坐标值（现在说有点抽象，所谓的变换就是缩放、旋转这种）。它是缩放、旋转等变换的中心点。从图像的展示效果上来看，如果锚点是(x, y)，则指定的是图片中(x, y)坐标的点与节点指定的position重合。

        在cocos中，锚点不是直接设定的，而是设定一个比例，比如 (0.3,  0.5)，然后在CCNode中，再根据内容大小 contentSize ，去乘以这个比例，确定锚点的真实坐标。这就是为什么在 《3.坐标系》中说到要使得锚点的设定有效，必须要设定content大小的原因，如果 contentSize 一直是0，那么无论你比例设置的是多少，锚点都始终在 CCPointZero。

4、子节点 -> 父节点

      根据上面的分析，可以将子节点坐标系到父节点坐标系的变换分解为以下几个动作，这里需要注意的是坐标系和坐标系中的内容之间相对独立的关系：

      （1）子节点的原点移动到锚点的位置，方便后面基于锚点的变换，这样原来坐标系下的坐标 (Ax, Ay)，在新的坐标系下就成了(0, 0)

      （2）在新的坐标系下进行缩放（这一步和3可以调换位置），缩放前的点 (1,1) ，缩放后成了 (Sx, Sy)

      （3）在2的基础上，进行旋转，注意代码中的这样一句

            float radians = -CC_DEGREES_TO_RADIANS(m_fRotation);

            也就是说，设置的 setRotation 的角度是 β°的话，实际应用在矩阵中的是 -β°，再注意到这个旋转矩阵的写法和OpenGL中的旋转矩阵完全一样。在默认的右手坐标系下，Z轴指向屏幕外，所以旋转正方向是逆时针，也就是逆时针旋转了 -β°，进一步， 就是顺时针旋转了 β°。出于方便的原因，除了这里， 本文中其他地方提到的β角度实际上都是-β。

      （4）将坐标系原点移动到 (-Px, -Py)，使得原来位于原点的图像，现在的坐标变成了 (Px, Py)。

      综合下来，（可以到第四节中查阅变换对应的齐次变换矩阵，实际上正好对应着式2-3分解的几个矩阵），由于递进的变换就是按照式2-1形式表示的矩阵的右乘，这样就得到了式(2-3)。

      这里再回答一个上面提出的问题，即为什么锚点指示着与positon重合的图片的点：看第四步就懂了，最终摆在position上的点，是在第三步中生成的坐标系的原点，而这个点就是锚点。由于锚点在2-3步变换中都是不受影响的（旋转、缩放什么的不会改变原点），所以它就来自于第一步的平移的结果，就是对应着在第一步操作之前的坐标系下的(Ax, Ay)的点，也就是图片上(Ax, Ay)点。

      这样说还有些麻烦，正向想更容易理解：图片上锚点位置点(Ax, Ay)，在第一步变换的时候成为了原点，在后续的缩放和旋转中不受影响，然后在第四步中，在新的坐标系下坐标值成了(Px, Py)，但是内容本身并不发生变化。

4、屏幕坐标系

      cocos中的屏幕坐标系，原点在显示框的左下角，正方向是右上，右手坐标系，单位是像素px。

      至于坐标是怎么从节点坐标系映射过来的，则很简单：如果你是根节点，假设  nodeToParentTransform = NtP，则节点中的某个点 (x, y)，对应着的屏幕上的点(x', y')有：

      (x', y') = (x, y) * NtP

     如果你是子节点，则 nodeToWorldTransform 是所有NtP的累乘：

CCAffineTransform CCNode::nodeToWorldTransform()
{
    CCAffineTransform t = this->nodeToParentTransform();

    for (CCNode *p = m_pParent; p != NULL; p = p->getParent())
        t = CCAffineTransformConcat(t, p->nodeToParentTransform());

    return t;
}

三、锚点坐标系？

       从上面的变换过程可以看到，如果把子节点到父节点的变换过程分解为两步，先平移到锚点看做第一步，则可以提取出锚点坐标系的概念。不过这个坐标系本身没有直接获取变换矩阵的方法，所以存在感并不强烈。不过有个方法 convertToNodeSpaceAR，用来将一个世界坐标系下的点 (x', y')，转换为这个所谓锚点坐标系下的坐标值 (x, y) 的方法。

        这个方法的实现相当简单，毕竟所谓的锚点坐标系也只是简单平移得到的：

CCPoint CCNode::convertToNodeSpaceAR(const CCPoint& worldPoint)
{
    CCPoint nodePoint = convertToNodeSpace(worldPoint);
    return ccpSub(nodePoint, m_tAnchorPointInPoints);
}

        必须要指出的是，所有目前我已知的，变换中涉及到坐标的，如 setPosition等，都是在节点坐标系下的值，和锚点本身并没有关系。

四、Z轴

       这一段是题外话，在 addChild中设定的 zOrder，是值越小，越在下面，这个和Z轴指向屏幕外是一样的。